Lesson 5

Describing Transformations

View Student Lesson

Problem 1

Here is Trapezoid A in the coordinate plane:

Trapezoid \(A\) on a coordinate plane, origin \(O\) . Horizontal and vertical axis scale negative 5 to 5 by 1’s. Trapezoid \(A\) has coordinates (2 comma 1), (2 comma 3), (4 comma 4) and (4 comma 1).
  1. Draw Polygon B, the image of A, using the \(y\)-axis as the line of reflection.
  2. Draw Polygon C, the image of B, using the \(x\)-axis as the line of reflection.
  3. Draw Polygon D, the image of C, using the \(x\)-axis as the line of reflection.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

The point \((\text{-}4,1)\) is rotated 180 degrees counterclockwise using center \((\text{-}3,0)\). What are the coordinates of the image?

A:

\((\text{-}5,\text{-}2)\)

B:

\((\text{-}4,\text{-}1)\)

C:

\((\text{-}2,\text{-}1)\)

D:

\((4,\text{-}1)\)

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Describe a sequence of transformations for which Triangle B is the image of Triangle A.

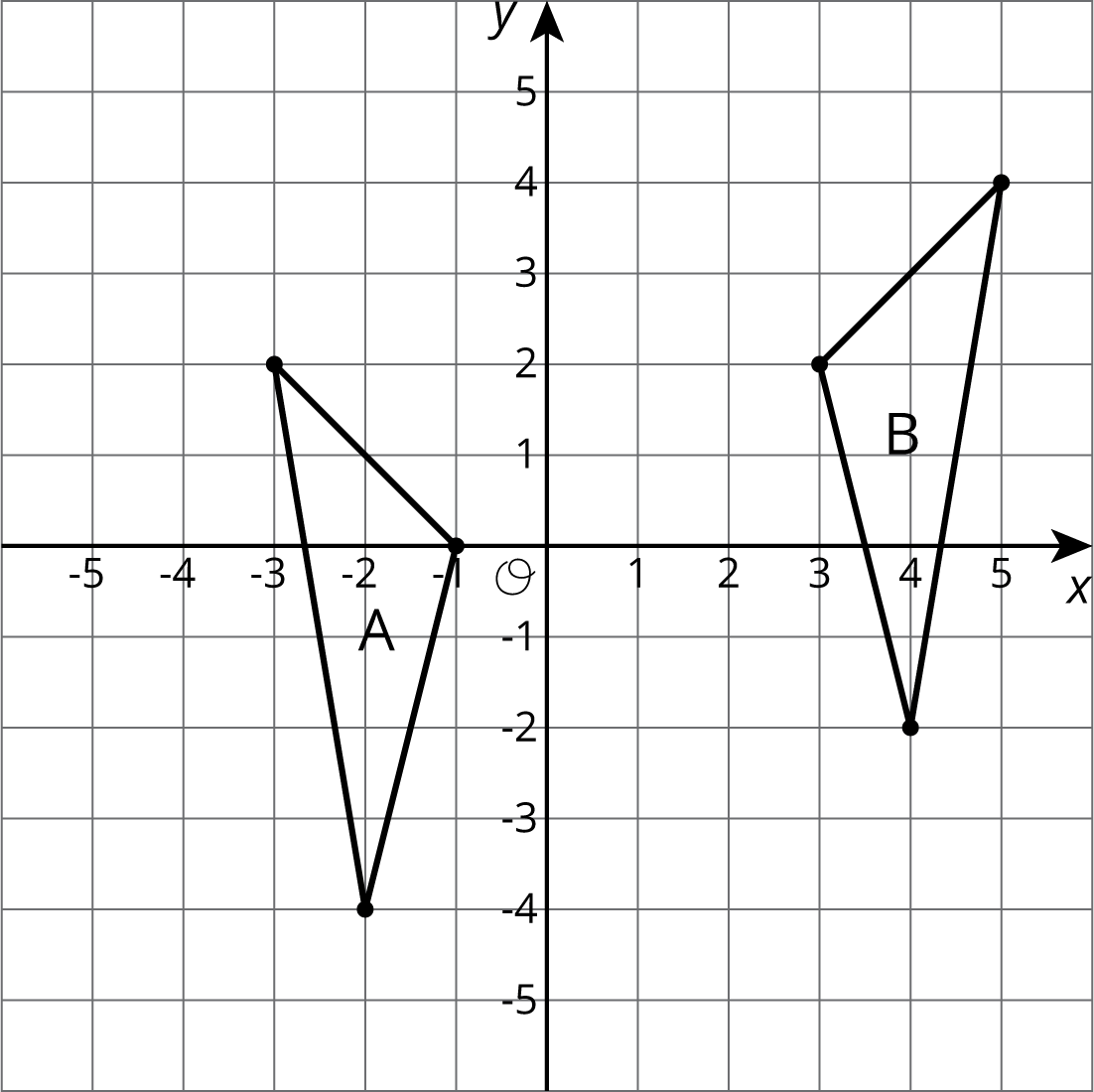
Triangle A and its image triangle B on a coordinate plane, origin \(O\). 

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Here is quadrilateral \(ABCD\).

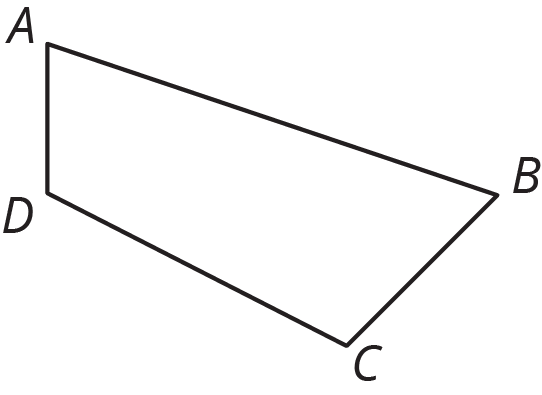
Quadrilateral A B C D. A B, A D and D C all have negative slopes. B C has a positive slope. A B C D has no parallel sides and no right angles.

 

Draw the image of quadrilateral \(ABCD\) after each transformation.

  1. The translation that takes \(B\) to \(D\).
  2. The reflection over segment \(BC\).
  3. The rotation about point \(A\) by angle \(DAB\), counterclockwise.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 2.)