Lesson 15

Building Polygons

View Student Lesson

Problem 1

A rectangle has side lengths of 6 units and 3 units. Could you make a quadrilateral that is not identical using the same four side lengths? If so, describe it.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Come up with an example of three side lengths that can not possibly make a triangle, and explain how you know.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

In the diagram, the length of segment \(AB\) is 10 units and the radius of the circle centered at \(A\) is 4 units. Use this to create two unique triangles, each with a side of length 10 and a side of length 4. Label the sides that have length 10 and 4.

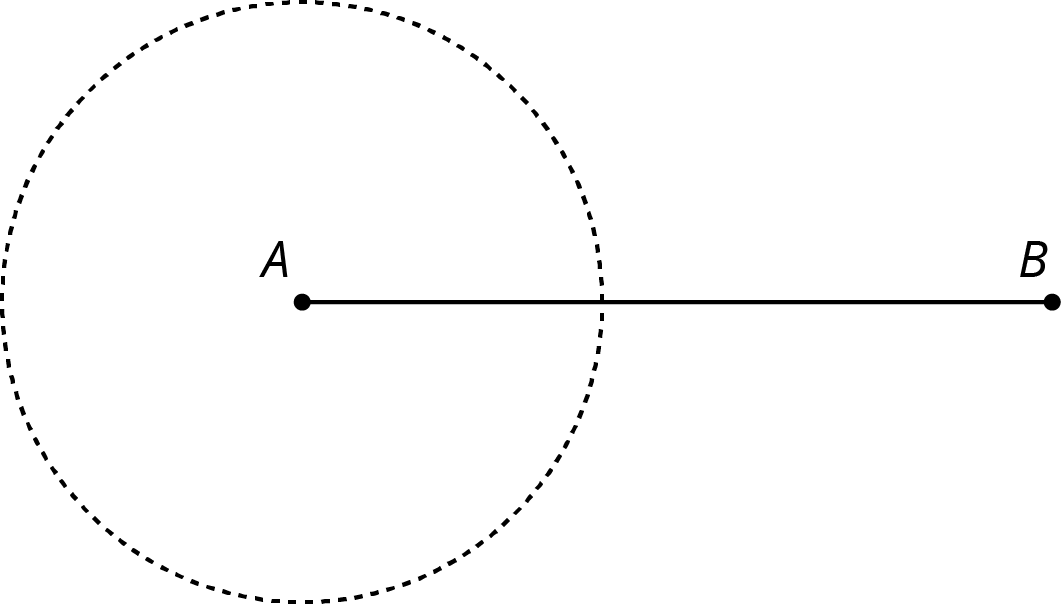
A line segment is labeled A  B.  A dotted circle is drawn with center at A.

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Select all the sets of three side lengths that will make a triangle.

A:

3, 4, 8

B:

7, 6, 12

C:

5, 11, 13

D:

4, 6, 12

E:

4, 6, 10

Solution

For access, consult one of our IM Certified Partners.

Problem 5

Based on signal strength, a person knows their lost phone is exactly 47 feet from the nearest cell tower. The person is currently standing 23 feet from the same cell tower. What is the closest the phone could be to the person? What is the furthest their phone could be from them?

Solution

For access, consult one of our IM Certified Partners.

Problem 6

Here is quadrilateral \(ABCD\).

 

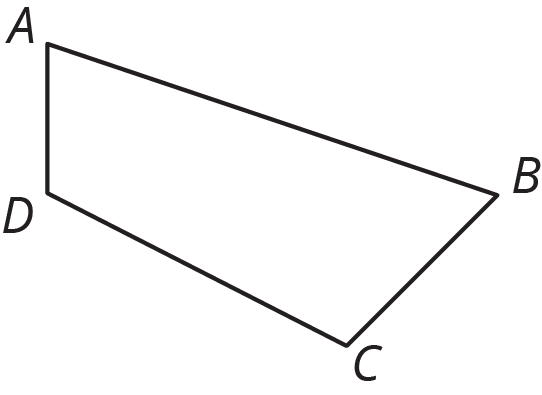
Quadrilateral A B C D. A B, A D and D C all have negative slopes. B C has a positive slope. A B C D has no parallel sides and no right angles.

 

Draw the image of quadrilateral \(ABCD\) after each rotation using \(B\) as center.

  1. 90 degrees clockwise
  2. 120 degrees clockwise
  3. 30 degrees counterclockwise

Solution

For access, consult one of our IM Certified Partners.

(From Unit 1, Lesson 2.)