Lesson 20
Dividing Decimals by Decimals
Problem 1
-
Explain why all of these expressions have the same value.
\(4.5 \div 0.09\)
\(45 \div 0.9\)
\(450 \div 9\)
\(4500\div 90\)
-
What is the common value?
Solution
For access, consult one of our IM Certified Partners.
Problem 2
A student said, “To find the value of \(109.2 \div 6\), I can divide 1,092 by 60.”
- Do you agree with her? Explain your reasoning.
-
Calculate the quotient of \(109.2 \div 6\) using any method of your choice.
Solution
For access, consult one of our IM Certified Partners.
Problem 3
Here is how Han found \(31.59 \div 13\):
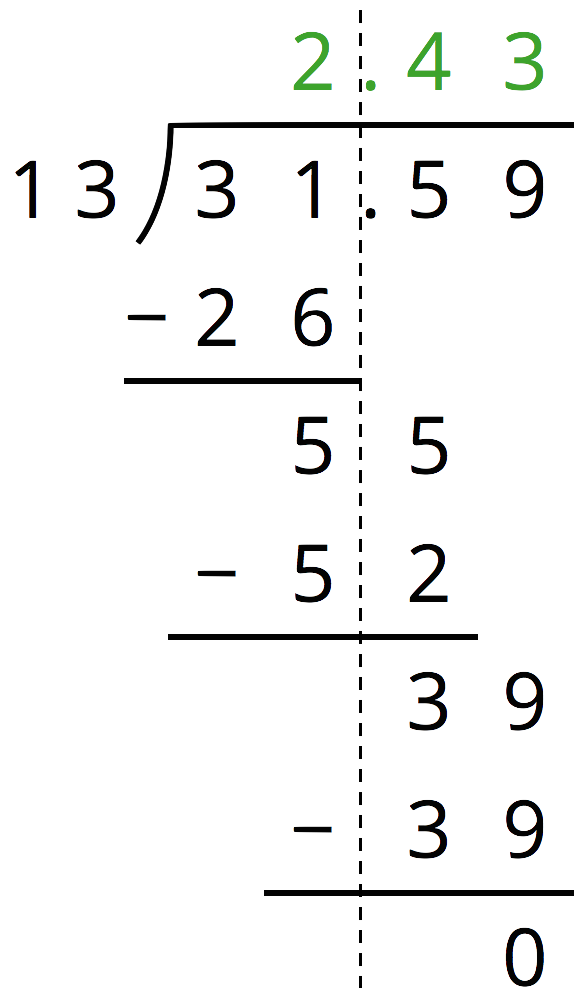
- At the second step, Han subtracts 52 from 55. How do you know that these numbers represent tenths?
- At the third step, Han subtracts 39 from 39. How do you know that these numbers represent hundredths?
- Check that Han’s answer is correct by calculating the product of 2.43 and 13.
Solution
For access, consult one of our IM Certified Partners.
Problem 4
- Write two division expressions that have the same value as \(61.12 \div 3.2\).
- Find the value of \(61.12 \div 3.2\). Show your reasoning.
Solution
For access, consult one of our IM Certified Partners.
Problem 5
Find each difference. If you get stuck, consider drawing a diagram.
Solution
For access, consult one of our IM Certified Partners.
(From Unit 3, Lesson 15.)Problem 6
At a school, 460 of the students walk to school.
- The number of students who take public transit is 20% of the number of students who walk. How many students take public transit?
- The number of students who bike to school is 5% of the number of students who walk. How many students bike to school?
- The number of students who ride the school bus is 110% of the number of students who walk. How many students ride the school bus?
Solution
For access, consult one of our IM Certified Partners.
(From Unit 2, Lesson 23.)