Lesson 11
Part-Part-Whole Ratios
Let’s look at situations where you can add the quantities in a ratio together.
Problem 1
Here is a tape diagram representing the ratio of red paint to yellow paint in a mixture of orange paint.
- What is the ratio of yellow paint to red paint?
- How many total cups of orange paint will this mixture yield?

Problem 2
At the kennel, the ratio of cats to dogs is \(4:5\). There are 27 animals in all. Here is a tape diagram representing this ratio.

- What is the value of each small rectangle?
- How many dogs are at the kennel?
- How many cats are at the kennel?
Problem 3
Last month, there were 4 sunny days for every rainy day. If there were 30 days in the month, how many days were rainy? Explain your reasoning. If you get stuck, consider using a tape diagram.
Problem 4
Noah entered a 100-mile bike race. He knows he can ride 32 miles in 160 minutes. At this rate, how long will it take him to finish the race? Use each table to find the answer. Next, explain which table you think works better in finding the answer.
Table A:
| distance (miles) | elapsed time (minutes) |
|---|---|
| 32 | 160 |
| 1 | |
| 100 |
Table B:
| distance (miles) | elapsed time (minutes) |
|---|---|
| 32 | 160 |
| 96 | |
| 4 | |
| 100 |
Problem 5
A cashier worked an 8-hour day, and earned $58.00. The double number line shows the amount she earned for working different numbers of hours. For each question, explain your reasoning.
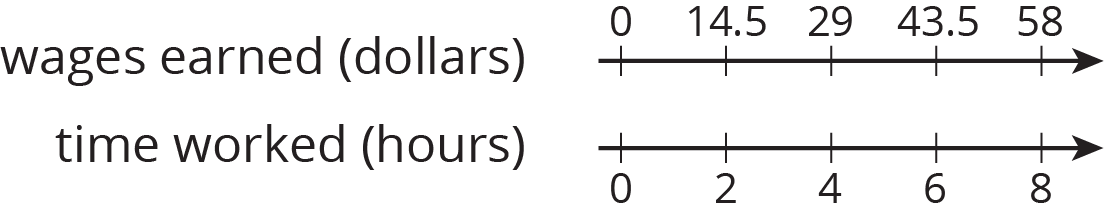
- How much does the cashier earn per hour?
- How much does the cashier earn if she works 3 hours?
Problem 6
A grocery store sells bags of oranges in two different sizes.
- The 3-pound bags of oranges cost $4.
- The 8-pound bags of oranges for $9.
Which oranges cost less per pound? Explain or show your reasoning.