Lesson 8

Representing Ratios with Tables

Let’s use tables to represent equivalent ratios.

8.1: How Is It Growing?

Look for a pattern in the figures.

  1. How many total tiles will be in:

    1. the 4th figure?
    2. the 5th figure?
    3. the 10th figure?

  2. How do you see it growing?

A growing pattern of tiles arranged in rows.

 

8.2: A Huge Amount of Sparkling Orange Juice

Noah’s recipe for one batch of sparkling orange juice uses 4 liters of orange juice and 5 liters of soda water.

  1. Use the double number line to show how many liters of each ingredient to use for different-sized batches of sparkling orange juice.

  2. If someone mixes 36 liters of orange juice and 45 liters of soda water, how many batches would they make?
  3. If someone uses 400 liters of orange juice, how much soda water would they need?
  4. If someone uses 455 liters of soda water, how much orange juice would they need?
  5. Explain the trouble with using a double number line diagram to answer the last two questions.

8.3: Batches of Trail Mix

A recipe for trail mix says: “Mix 7 ounces of almonds with 5 ounces of raisins.” Here is a table that has been started to show how many ounces of almonds and raisins would be in different-sized batches of this trail mix.

almonds (oz) raisins (oz)
7 5
28
10
3.5
250
56

  1. Complete the table so that ratios represented by each row are equivalent.

  2. What methods did you use to fill in the table?
  3. How do you know that each row shows a ratio that is equivalent
    to \(7:5\)? Explain your reasoning.


You have created a best-selling recipe for chocolate chip cookies. The ratio of sugar to flour is \(2:5\).

Create a table in which each entry represents amounts of sugar and flour that might be used at the same time in your recipe.

  • One entry should have amounts where you have fewer than 25 cups of flour.
  • One entry should have amounts where you have between 20–30 cups of sugar.
  • One entry can have any amounts using more than 500 units of flour.

Summary

A table is a way to organize information. Each horizontal set of entries is called a row, and each vertical set of entries is called a column. (The table shown has 2 columns and 5 rows.) A table can be used to represent a collection of equivalent ratios.

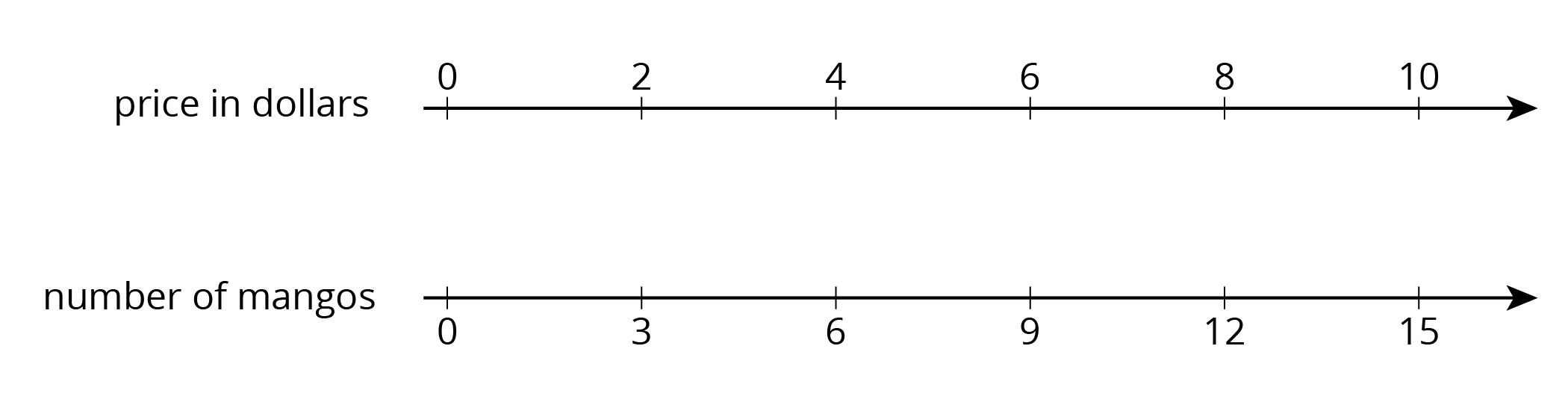
Here is a double number line diagram and a table that both represent the situation: “The price is \$2 for every 3 mangos.”

A double number line with 6 evenly spaced tick marks: For "price in dollars" the numbers 0, 2, 4, 6, 8, and 10 are indicated. For "number of mangos" the numbers 0, 3, 6, 9, 12, and 15 are indicated.
2-column table, 5 rows of data. First column labeled "price in dollars,” second column labeled "number of mangos." The data is as follows: Row 1: 2, 3 Row 2: 4, 6 Row 3: 6, 9 Row 4: 8, 12 Row 5: 10, 15.

Glossary Entries

  • double number line diagram

    A double number line diagram uses a pair of parallel number lines to represent equivalent ratios. The locations of the tick marks match on both number lines. The tick marks labeled 0 line up, but the other numbers are usually different.

    A double number line for teaspoons of red paint: 0, 3, 6, 9, 12 and teaspoons of yellow paint: 0, 5, 10, 15, 20.
  • per

    The word per means “for each.” For example, if the price is $5 per ticket, that means you will pay $5 for each ticket. Buying 4 tickets would cost $20, because \(4 \boldcdot 5 = 20\).

  • same rate

    We use the words same rate to describe two situations that have equivalent ratios.

    For example, a sink is filling with water at a rate of 2 gallons per minute. If a tub is also filling with water at a rate of 2 gallons per minute, then the sink and the tub are filling at the same rate.

  • table

    A table organizes information into horizontal rows and vertical columns. The first row or column usually tells what the numbers represent.

    For example, here is a table showing the tail lengths of three different pets. This table has four rows and two columns.

    pet tail length (inches)
    dog 22
    cat 12
    mouse 2