Lesson 23
Solving Percentage Problems
23.1: Number Talk: Decimals
Find the value of each expression mentally.
\((0.23) \boldcdot 100\)
\(50 \div 100\)
\(145 \boldcdot \frac{1}{100}\)
\(7 \div 100\)
23.2: Info Gap: Music Devices
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
-
Silently read your card and think about what information you need to be able to answer the question.
-
Ask your partner for the specific information that you need.
-
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
-
Share the problem card and solve the problem independently.
-
Read the data card and discuss your reasoning.
If your teacher gives you the data card:
-
Silently read your card.
-
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
-
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
-
Read the problem card and solve the problem independently.
-
Share the data card and discuss your reasoning.
23.3: Everything is On Sale
During a sale, every item in a store is 80% of its regular price.
- If the regular price of a T-shirt is $10, what is its sale price?
- The regular prices of five items are shown here. Find the sale price of each item.
item 1 item 2 item 3 item 4 item 5 regular price $1 $4 $10 $55 $120 sale price -
You found 80% of many values. Was there a process you repeated over and over to find the sale prices? If so, describe it.
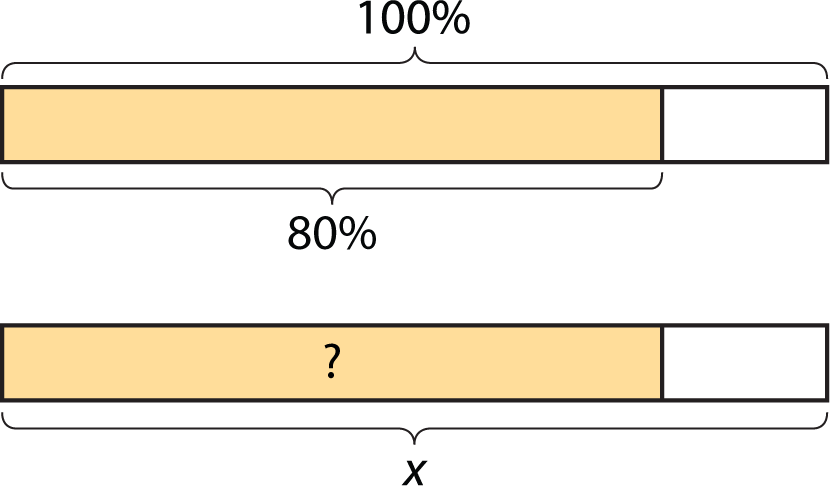
-
Select all of the expressions that could be used to find 80% of \(x\). Be prepared to explain your reasoning.
\(\frac{8}{100} \boldcdot x\)
\(\frac{80}{100} \boldcdot x\)
\(\frac{8}{10} \boldcdot x\)
\(\frac{4}{10} \boldcdot x\)
\(\frac85 \boldcdot x\)
\(\frac45 \boldcdot x\)
\(80 \boldcdot x\)
\(8 \boldcdot x\)
\((0.8) \boldcdot x\)
\((0.08) \boldcdot x\)
Summary
A pot holds 36 liters of water. 25% of 36 liters is 9 liters. Here are two different representations that display this information:
- A double number line:

We can divide the distance between 0 and 36 into four equal intervals to show that 9 is \(\frac{1}{4}\) of 36, or 9 is 25% of 36.
- A table:
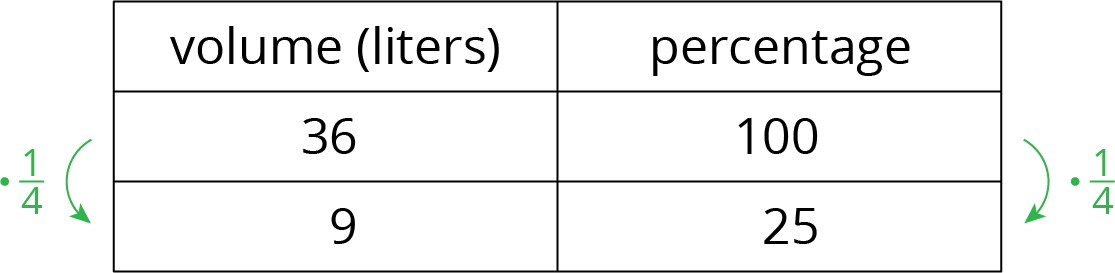
In the case of the table, notice that the rows are multiplied by \(\frac{1}{4}\) which is equivalent to \(\frac{25}{100}\).
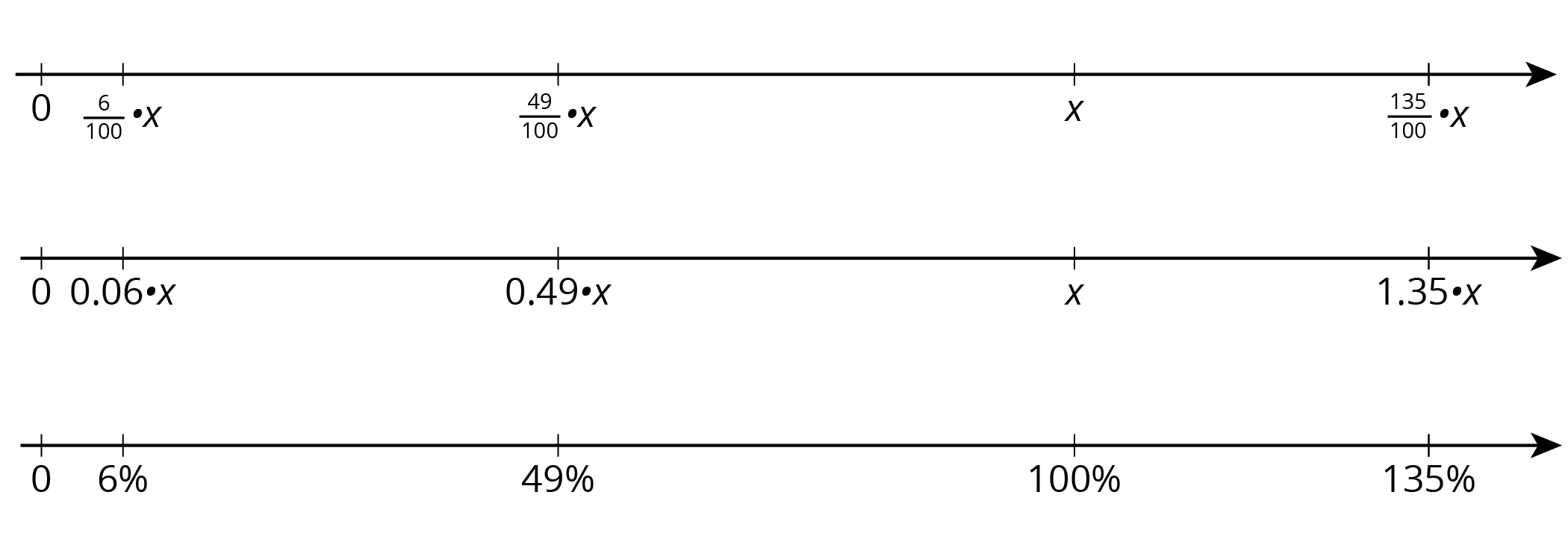
In general, to find \(P\%\) of \(x\), we can multiply: \(\frac{P}{100}\boldcdot x\).
- To find 49% of a number, we can multiply the number by \(\frac{49}{100}\) or 0.49.
- To find 135% of a number, we can multiply the number by \(\frac{135}{100}\) or 1.35.
- To find 6% of a number, we can multiply the number by \(\frac{6}{100}\) or 0.06.
Glossary Entries
- percent
The word percent means “for each 100.” The symbol for percent is %.
For example, a quarter is worth 25 cents, and a dollar is worth 100 cents. We can say that a quarter is worth 25% of a dollar.


- percentage
A percentage is a rate per 100.
For example, a fish tank can hold 36 liters. Right now there is 27 liters of water in the tank. The percentage of the tank that is full is 75%.
