Lesson 15
Infinite Decimal Expansions
Problem 1
Elena and Han are discussing how to write the repeating decimal \(x = 0.13\overline{7}\) as a fraction. Han says that \(0.13\overline{7}\) equals \(\frac{13764}{99900}\). “I calculated \(1000x = 137.77\overline{7}\) because the decimal begins repeating after 3 digits. Then I subtracted to get \(999x = 137.64\). Then I multiplied by \(100\) to get rid of the decimal: \(99900x = 13764\). And finally I divided to get \(x = \frac{13764}{99900}\).” Elena says that \(0.13\overline{7}\) equals \(\frac{124}{900}\). “I calculated \(10x = 1.37\overline{7}\) because one digit repeats. Then I subtracted to get \(9x = 1.24\). Then I did what Han did to get \(900x = 124\) and \(x = \frac{124}{900}\).”
Do you agree with either of them? Explain your reasoning.
Solution
For access, consult one of our IM Certified Partners.
Problem 2
How are the numbers \(0.444\) and \(0.\overline{4}\) the same? How are they different?
Solution
For access, consult one of our IM Certified Partners.
Problem 3
- Write each fraction as a decimal.
-
\(\frac{2}{3}\)
-
\(\frac{126}{37}\)
-
-
Write each decimal as a fraction.
-
\(0.\overline{75}\)
-
\(0.\overline{3}\)
-
Solution
For access, consult one of our IM Certified Partners.
Problem 4
Write each fraction as a decimal.
-
\(\frac{5}{9}\)
-
\(\frac{5}{4}\)
-
\(\frac{48}{99}\)
-
\(\frac{5}{99}\)
-
\(\frac{7}{100}\)
-
\(\frac{53}{90}\)
Solution
For access, consult one of our IM Certified Partners.
Problem 5
Write each decimal as a fraction.
-
\(0.\overline{7}\)
-
\(0.\overline{2}\)
-
\(0.1\overline{3}\)
-
\(0.\overline{14}\)
-
\(0.\overline{03}\)
-
\(0.6\overline{38}\)
-
\(0.52\overline{4}\)
-
\(0.1\overline{5}\)
Solution
For access, consult one of our IM Certified Partners.
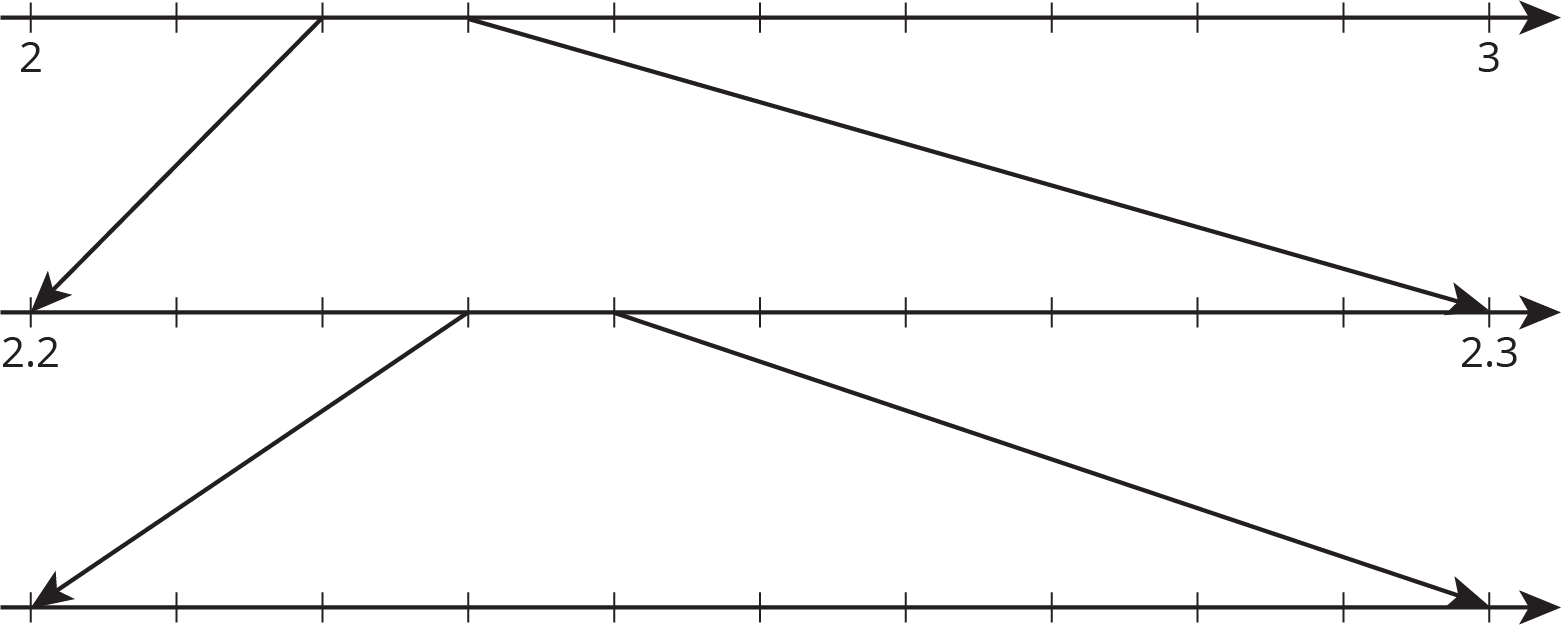
Problem 6
\(2.2^2 = 4.84\) and \(2.3^2 = 5.29\). This gives some information about \(\sqrt 5\).
Without directly calculating the square root, plot \(\sqrt{5}\) on all three number lines using successive approximation.
Solution
For access, consult one of our IM Certified Partners.