Lesson 10
Applications of the Pythagorean Theorem
Problem 1
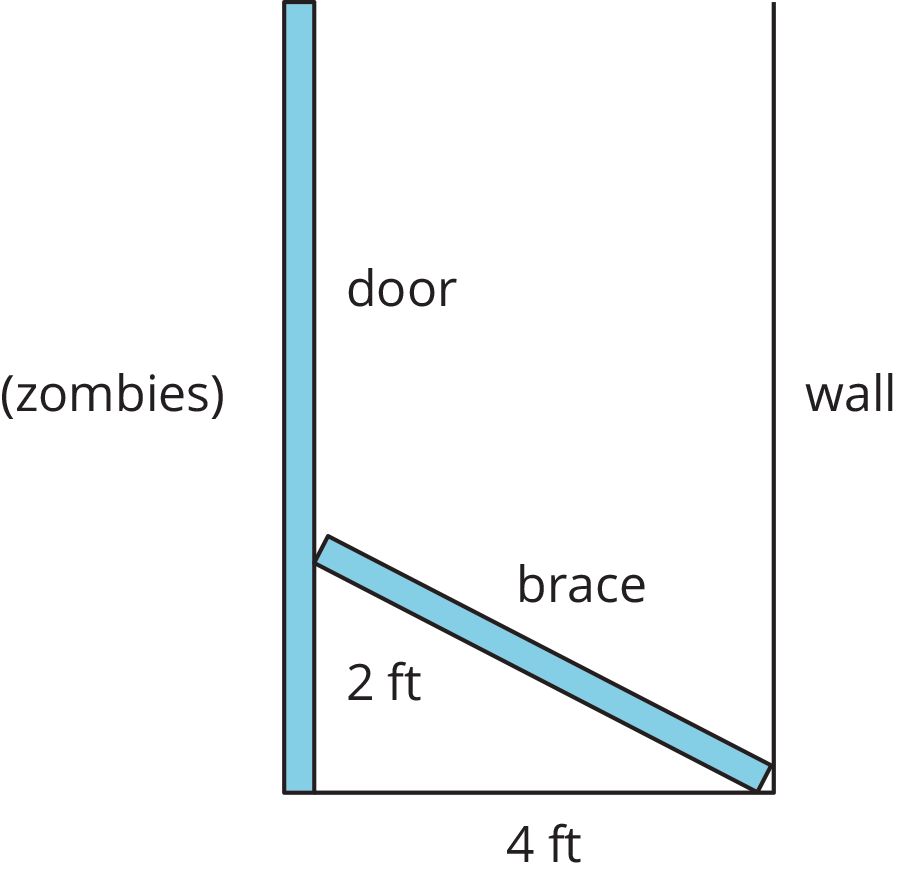
A man is trying to zombie-proof his house. He wants to cut a length of wood that will brace a door against a wall. The wall is 4 feet away from the door, and he wants the brace to rest 2 feet up the door. About how long should he cut the brace?
Solution
For access, consult one of our IM Certified Partners.
Problem 2
At a restaurant, a trash can’s opening is rectangular and measures 7 inches by 9 inches. The restaurant serves food on trays that measure 12 inches by 16 inches. Jada says it is impossible for the tray to accidentally fall through the trash can opening because the shortest side of the tray is longer than either edge of the opening. Do you agree or disagree with Jada’s explanation? Explain your reasoning.
Solution
For access, consult one of our IM Certified Partners.
Problem 3
Select all the sets that are the three side lengths of right triangles.
8, 7, 15
4, 10, \(\sqrt{84}\)
\(\sqrt{8}\), 11, \(\sqrt{129}\)
\(\sqrt{1}\), 2, \(\sqrt{3}\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 8, Lesson 9.)Problem 4
For each pair of numbers, which of the two numbers is larger? How many times larger?
- \(12 \boldcdot 10^9\) and \(4 \boldcdot 10^9\)
- \(1.5 \boldcdot 10^{12}\) and \(3 \boldcdot 10^{12}\)
- \(20 \boldcdot 10^4\) and \(6 \boldcdot 10^5\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 7, Lesson 10.)Problem 5
A line contains the point \((3,5)\). If the line has negative slope, which of these points could also be on the line?
\((2,0)\)
\((4,7)\)
\((5,4)\)
\((6,5)\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 3, Lesson 10.)Problem 6
Noah and Han are preparing for a jump rope contest. Noah can jump 40 times in 0.5 minutes. Han can jump \(y\) times in \(x\) minutes, where \(y = 78x\). If they both jump for 2 minutes, who jumps more times? How many more?
Solution
For access, consult one of our IM Certified Partners.
(From Unit 3, Lesson 4.)