Lesson 8
Combining Bases
Let’s multiply expressions with different bases.
Problem 1
Select all the true statements:
\(2^8 \boldcdot 2^9 = 2^{17}\)
\(8^2 \boldcdot 9^2 = 72^2\)
\(8^2 \boldcdot 9^2 = 72^4\)
\(2^8 \boldcdot 2^9 = 4^{17}\)
Problem 2
Find \(x\), \(y\), and \(z\) if \((3 \boldcdot 5)^4 \boldcdot (2 \boldcdot 3)^5 \boldcdot (2 \boldcdot 5)^7 = 2^x \boldcdot 3^y \boldcdot 5^z\).
Problem 3
Han found a way to compute complicated expressions more easily. Since \(2 \boldcdot 5 = 10\), he looks for pairings of 2s and 5s that he knows equal 10. For example, \(3 \boldcdot 2^4 \boldcdot 5^5 = 3 \boldcdot 2^4 \boldcdot 5^4 \boldcdot 5 = (3 \boldcdot 5) \boldcdot (2 \boldcdot 5)^4 = 15 \boldcdot 10^4 = 150,\!000.\) Use Han's technique to compute the following:
- \(2^4 \boldcdot 5 \boldcdot (3 \boldcdot 5)^3\)
- \(\frac{2^3 \boldcdot 5^2 \boldcdot (2 \boldcdot 3)^2 \boldcdot (3 \boldcdot 5)^2}{3^2}\)
Problem 4
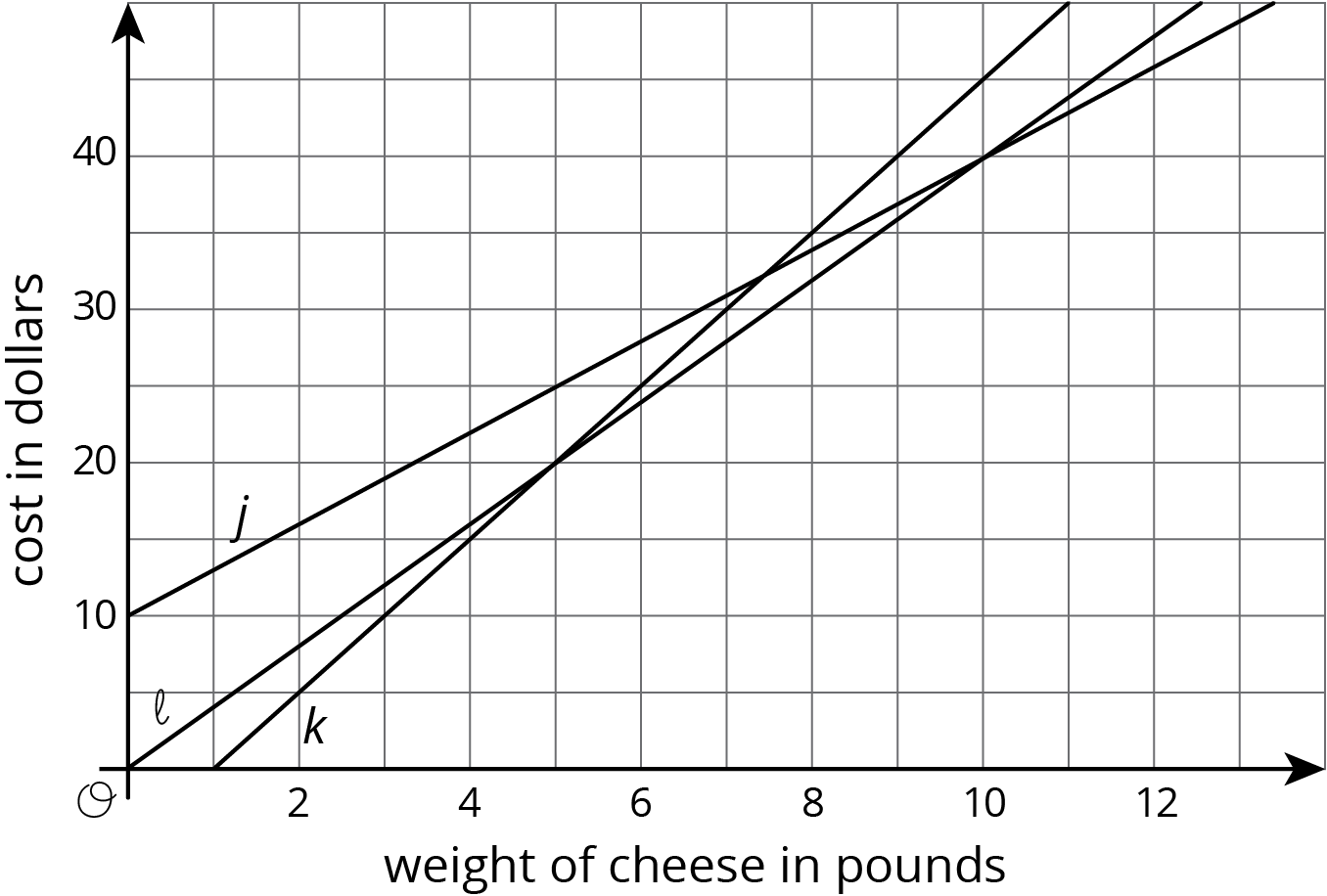
The cost of cheese at three stores is a function of the weight of the cheese. The cheese is not prepackaged, so a customer can buy any amount of cheese.
-
Store A sells the cheese for \(a\) dollars per pound.
-
Store B sells the same cheese for \(b\) dollars per pound and a customer has a coupon for $5 off the total purchase at that store.
-
Store C is an online store, selling the same cheese at \(c\) dollar per pound, but with a $10 delivery fee.
This graph shows the price functions for stores A, B, and C.
-
Match Stores A, B, and C with Graphs \(j\), \(k\), and \(\ell\).
-
How much does each store charge for the cheese per pound?
-
How many pounds of cheese does the coupon for Store B pay for?
-
Which store has the lowest price for a half a pound of cheese?
-
If a customer wants to buy 5 pounds of cheese for a party, which store has the lowest price?
-
How many pounds would a customer need to order to make Store C a good option?