Lesson 5
Negative Exponents with Powers of 10
Let’s see what happens when exponents are negative.
5.1: Number Talk: What's That Exponent?
Solve each equation mentally.
\(\frac{100}{1} = 10^x\)
\(\frac{100}{x} = 10^1\)
\(\frac{x}{100} = 10^0\)
\(\frac{100}{1,\!000} = 10^{x}\)
5.2: Negative Exponent Table
Complete the table to explore what negative exponents mean.
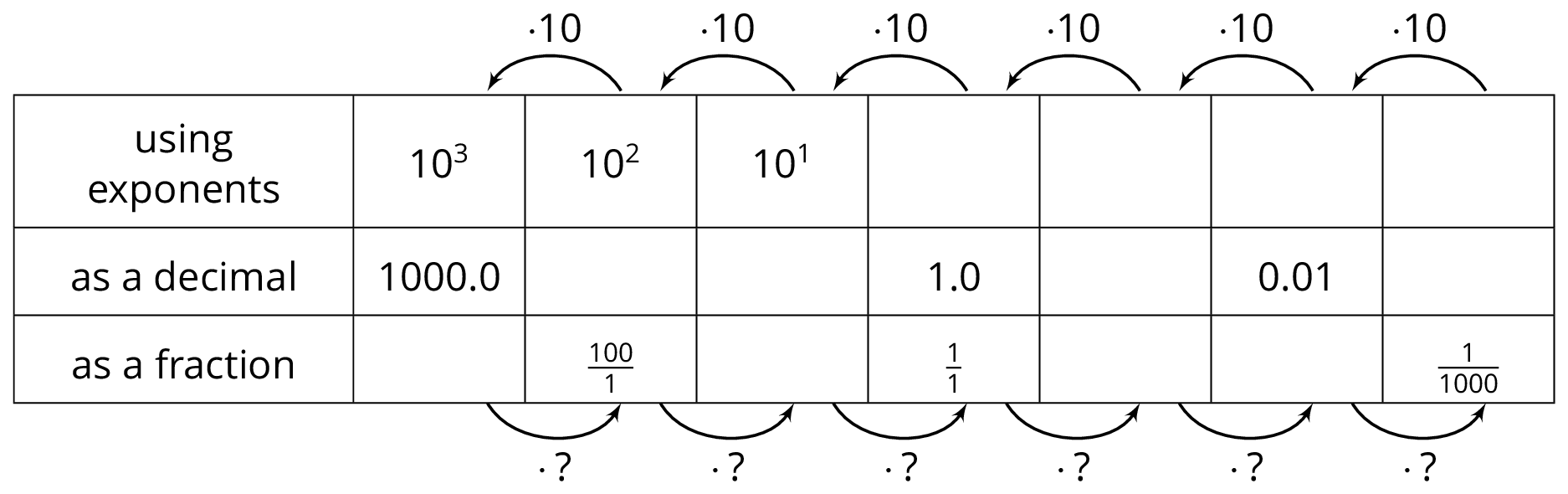
- As you move toward the left, each number is being multiplied by 10. What is the multiplier as you move right?
- How does a multiplier of 10 affect the placement of the decimal in the product? How does the other multiplier affect the placement of the decimal in the product?
- Use the patterns you found in the table to write \(10^{\text -7}\) as a fraction.
- Use the patterns you found in the table to write \(10^{\text -5}\) as a decimal.
- Write \(\frac{1}{100,000,000}\) using a single exponent.
- Use the patterns in the table to write \(10^{\text -n}\) as a fraction.
5.3: Follow the Exponent Rules
-
-
Match each exponential expression with an equivalent multiplication expression:
\(\left(10^2\right)^3\)\(\left(10^2\right)^{\text -3}\)
\(\left(10^{\text -2}\right)^3\)
\(\left(10^{\text -2}\right)^{\text-3}\)
\(\frac{1}{(10 \boldcdot 10)} \boldcdot \frac{1}{(10 \boldcdot 10)} \boldcdot \frac{1}{(10 \boldcdot 10)}\) \(\left(\frac{1}{10} \boldcdot \frac{1}{10}\right)\left(\frac{1}{10} \boldcdot \frac{1}{10}\right)\left(\frac{1}{10} \boldcdot \frac{1}{10}\right)\) \(\frac{1}{ \frac{1}{10} \boldcdot \frac{1}{10} }\boldcdot \frac{1}{ \frac{1}{10} \boldcdot \frac{1}{10} } \boldcdot \frac{1}{ \frac{1}{10} \boldcdot \frac{1}{10} }\) \((10 \boldcdot 10)(10 \boldcdot 10)(10 \boldcdot 10)\) - Write \((10^2)^{\text-3}\) as a power of 10 with a single exponent. Be prepared to explain your reasoning.
-
-
-
Match each exponential expression with an equivalent multiplication expression:
\(\frac{10^2}{10^5}\)\(\frac{10^2}{10^{\text -5}}\)
\(\frac{10^{\text -2}}{10^5}\)
\(\frac{10^{\text -2}}{10^{\text -5}}\)
\(\frac{ \frac{1}{10} \boldcdot \frac{1}{10} }{ \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}\boldcdot \frac{1}{10}\boldcdot \frac{1}{10} }\) \(\frac{10 \boldcdot 10}{10 \boldcdot 10 \boldcdot 10 \boldcdot 10 \boldcdot 10}\) \(\frac{ \frac{1}{10} \boldcdot \frac{1}{10} }{ 10 \boldcdot 10\boldcdot 10\boldcdot 10\boldcdot 10 }\) \(\frac{ 10 \boldcdot 10 }{ \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}\boldcdot \frac{1}{10}\boldcdot \frac{1}{10}}\) - Write \(\frac{10^{\text -2}}{10^{\text -5}}\) as a power of 10 with a single exponent. Be prepared to explain your reasoning.
-
-
-
Match each exponential expression with an equivalent multiplication expression:
\(10^4 \boldcdot 10^3\)\(10^4 \boldcdot 10^{\text -3}\)
\(10^{\text -4} \boldcdot 10^3\)
\(10^{\text -4} \boldcdot 10^{\text -3}\)
\((10 \boldcdot 10 \boldcdot 10 \boldcdot 10) \boldcdot ( \frac{1}{10} \boldcdot \frac{1}{10}\boldcdot \frac{1}{10})\) \(\left(\frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}\right) \boldcdot \left( \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}\right)\) \(\left(\frac{1}{10}\boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}\right) \boldcdot \left(10 \boldcdot 10 \boldcdot 10\right)\) \((10 \boldcdot 10 \boldcdot 10 \boldcdot 10) \boldcdot (10 \boldcdot 10 \boldcdot 10)\) - Write \(10^{\text-4} \boldcdot 10^3\) as a power of 10 with a single exponent. Be prepared to explain your reasoning.
-
Priya, Jada, Han, and Diego stand in a circle and take turns playing a game.
Priya says, SAFE. Jada, standing to Priya's left, says, OUT and leaves the circle. Han is next: he says, SAFE. Then Diego says, OUT and leaves the circle. At this point, only Priya and Han are left. They continue to alternate. Priya says, SAFE. Han says, OUT and leaves the circle. Priya is the only person left, so she is the winner.
Priya says, “I knew I’d be the only one left, since I went first.”
- Record this game on paper a few times with different numbers of players. Does the person who starts always win?
- Try to find as many numbers as you can where the person who starts always wins. What patterns do you notice?
Summary
When we multiply a positive power of 10 by \(\frac{1}{10}\), the exponent decreases by 1: \(\displaystyle 10^8 \boldcdot \frac{1}{10} = 10^7\)This is true for any positive power of 10. We can reason in a similar way that multiplying by 2 factors that are \(\frac{1}{10}\) decreases the exponent by 2: \(\displaystyle \left(\frac{1}{10}\right)^2 \boldcdot 10^8 = 10^6\)
That means we can extend the rules to use negative exponents if we make \(10^{\text-2} = \left(\frac{1}{10}\right)^2\). Just as \(10^2\) is two factors that are 10, we have that \(10^{\text-2}\) is two factors that are \(\frac{1}{10}\). More generally, the exponent rules we have developed are true for any integers \(n\) and \(m\) if we make \(\displaystyle 10^{\text-n} = \left(\frac{1}{10}\right)^n = \frac{1}{10^n}\)
Here is an example of extending the rule \(\frac{10^n}{10^m} = 10^{n-m}\) to use negative exponents: \(\displaystyle \frac{10^3}{10^5} = 10^{3-5} = 10^{\text-2}\) To see why, notice that \(\displaystyle \frac{10^3}{10^5} = \frac{10^3}{10^3 \boldcdot 10^2} = \frac{10^3}{10^3} \boldcdot \frac{1}{10^2} = \frac{1}{10^2}\)which is equal to \(10^{\text-2}\).
Here is an example of extending the rule \(\left(10^m\right)^n = 10^{m \boldcdot n}\) to use negative exponents: \(\displaystyle \left(10^{\text-2}\right)^{3} = 10^{(\text-2)(3)}=10^{\text-6}\)To see why, notice that \(10^{\text-2} = \frac{1}{10} \boldcdot \frac{1}{10}\). This means that \(\displaystyle \left(10^{\text-2}\right)^{3} =\left( \frac{1}{10} \boldcdot \frac{1}{10}\right)^3 = \left(\frac{1}{10} \boldcdot \frac{1}{10}\right) \boldcdot \left( \frac{1}{10} \boldcdot \frac{1}{10}\right)\boldcdot \left(\frac{1}{10}\boldcdot \frac{1}{10}\right) = \frac{1}{10^6} = 10^{\text-6}\)
Glossary Entries
- base (of an exponent)
In expressions like \(5^3\) and \(8^2\), the 5 and the 8 are called bases. They tell you what factor to multiply repeatedly. For example, \(5^3\) = \(5 \boldcdot 5 \boldcdot 5\), and \(8^2 = 8 \boldcdot 8\).