Lesson 5

Negative Exponents with Powers of 10

Let’s see what happens when exponents are negative.

Problem 1

Write with a single exponent: (ex: \(\frac{1}{10} \boldcdot \frac{1}{10} = 10^{\text-2}\))

  1. \(\frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}\)
  2. \(\frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}\)
  3. \((\frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10})^2\)
  4. \((\frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10})^3\)
  5. \((10 \boldcdot 10 \boldcdot 10)^{\text-2}\)

Problem 2

Write each expression as a single power of 10.

  1. \(10^{\text-3} \boldcdot 10^{\text-2}\)
  2. \(10^4 \boldcdot 10^{\text-1}\)
  3. \(\frac{10^5}{10^7}\)
  4. \((10^{\text-4})^5\)
  5. \(10^{\text-3} \boldcdot 10^{\text2}\)
  6. \(\frac{10^{\text-9}}{10^5}\)

Problem 3

Select all of the following that are equivalent to \(\frac{1}{10,000}\):

A:

\((10,\!000)^{\text-1}\)

B:

\((\text{-}10,\!000)\)

C:

\((100)^{\text-2}\)

D:

\((10)^{\text-4}\)

E:

\((\text{-}10)^2\)

Problem 4

Match each equation to the situation it describes. Explain what the constant of proportionality means in each equation.

Equations:

  1. \(y=3x\)
  2. \(\frac12x=y\)
  3. \(y=3.5x\)
  4. \(y=\frac52x\)

Situations:

  • A dump truck is hauling loads of dirt to a construction site. After 20 loads, there are 70 square feet of dirt.

  • I am making a water and salt mixture that has 2 cups of salt for every 6 cups of water.

  • A store has a “4 for $10” sale on hats.

  • For every 48 cookies I bake, my students get 24.

(From Unit 3, Lesson 2.)

Problem 5

  1. Explain why triangle \(ABC\) is similar to \(EDC\). 

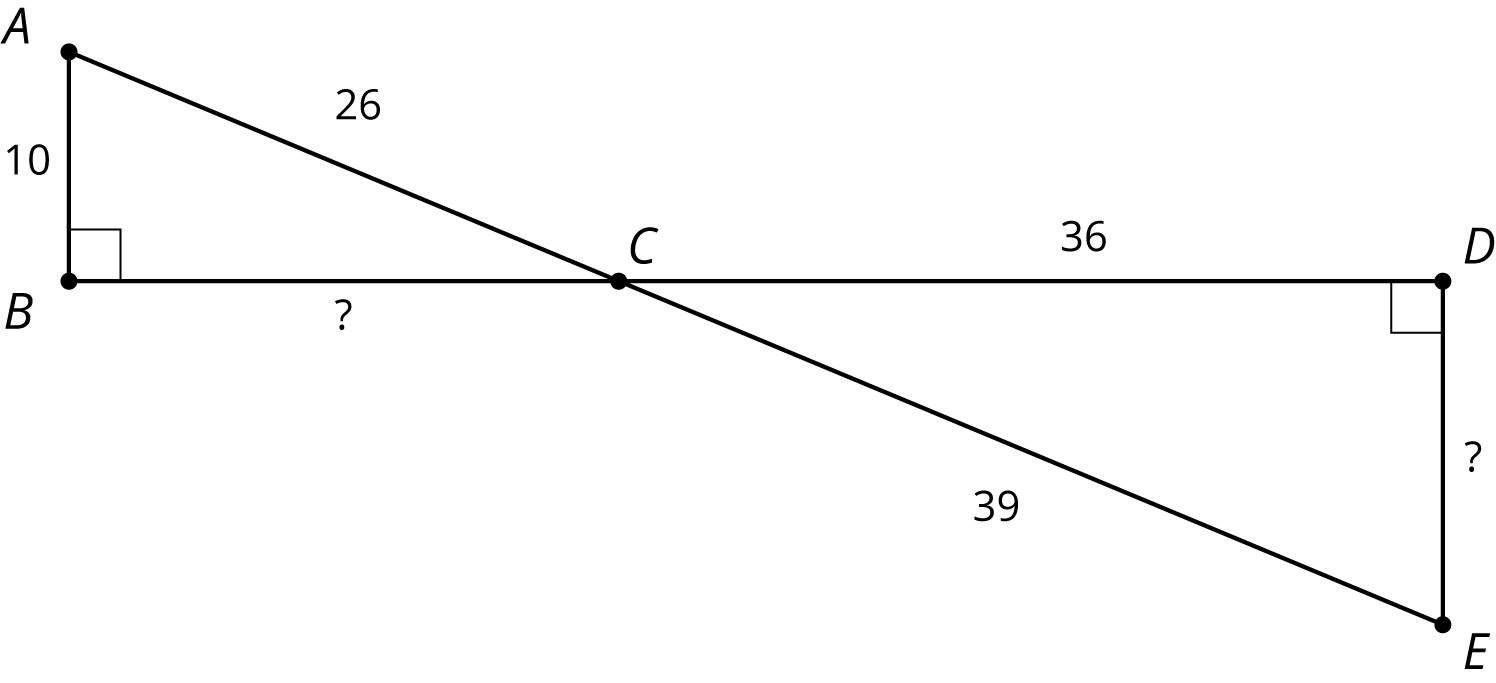
    Points B C D form a line. Points A, C E form a line. A, B is perpendicular to B C. D E is perpendicular to D C. Side A, B, length 10, side A, C, length 26, side C D, length 36, side C E length 39.
  2. Find the missing side lengths.
(From Unit 2, Lesson 8.)