Lesson 13

Definition of Scientific Notation

Let’s use scientific notation to describe large and small numbers.

Problem 1

Write each number in scientific notation.

  1. 14,700
  2. 0.00083
  3. 760,000,000
  4. 0.038
  5. 0.38
  6. 3.8
  7. 3,800,000,000,000
  8. 0.0000000009

Problem 2

Perform the following calculations. Express your answers in scientific notation.

  1. \((2 \times 10^5) + (6 \times 10^5)\)
     
  2. \((4.1 \times 10^7) \boldcdot 2\)
     
  3. \((1.5 \times 10^{11}) \boldcdot 3\)
     
  4. \((3 \times 10^3)^2\)
     
  5. \((9 \times 10^6) \boldcdot (3 \times 10^6)\)

Problem 3

Jada is making a scale model of the solar system. The distance from Earth to the Moon is about \(2.389 \times 10^5\) miles. The distance from Earth to the Sun is about \(9.296 \times 10^7\) miles. She decides to put Earth on one corner of her dresser and the Moon on another corner, about a foot away. Where should she put the sun?

  • On a windowsill in the same room?
  • In her kitchen, which is down the hallway?
  • A city block away?

Explain your reasoning.

Problem 4

Here is the graph for one equation in a system of equations.

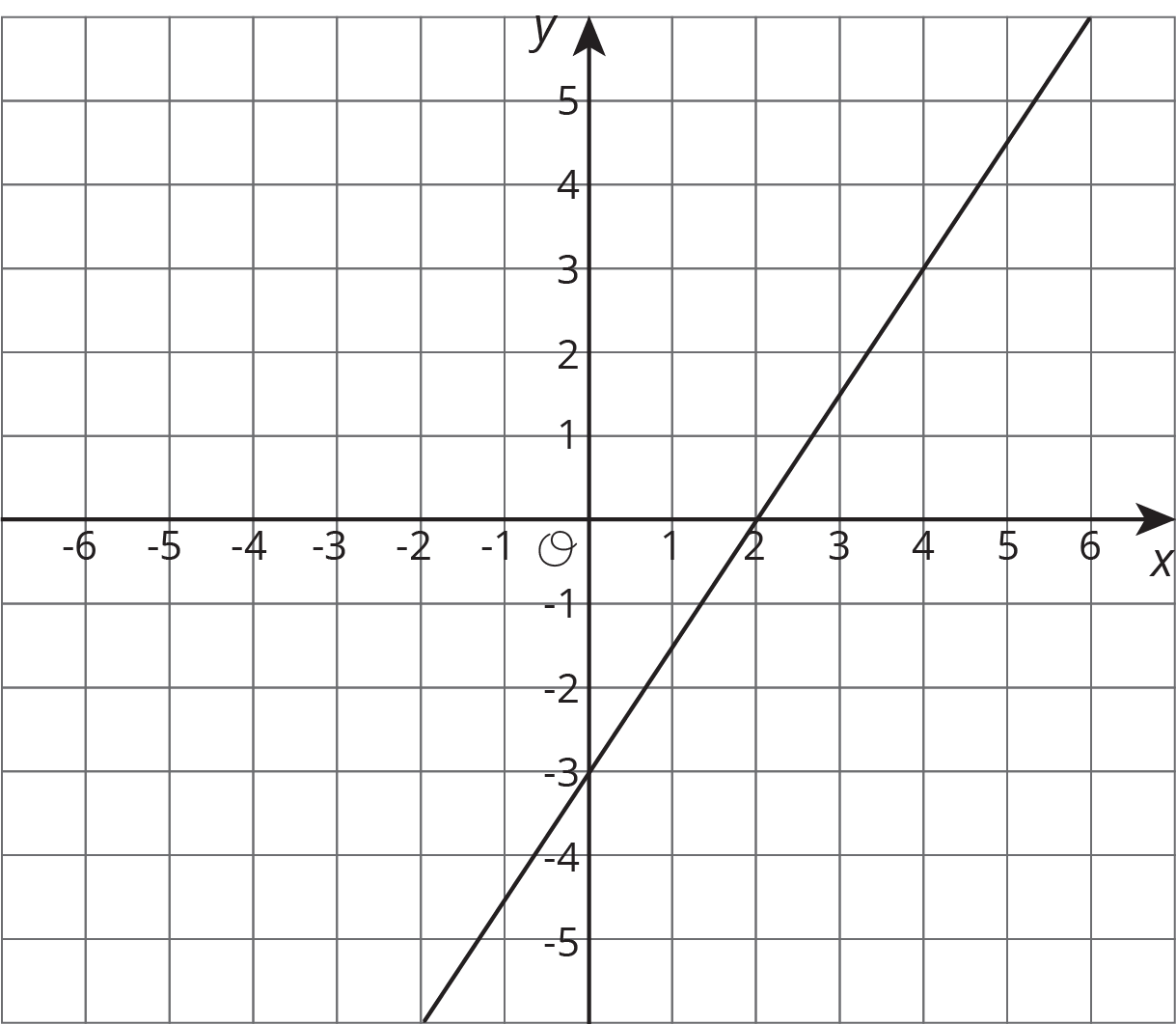
Coordinate plane, x, negative 6 to 6 by 1, y, negative 5 to 5 by 1. A line through negative 2 comma negative 6, 0 comma negative 3, 2 comma 0, 4 comma 3.
  1. Write a second equation for the system so it has infinitely many solutions.
  2. Write a second equation whose graph goes through \((0,2)\) so that the system has no solutions.
  3. Write a second equation whose graph goes through \((2,2)\) so that the system has one solution at \((4,3)\).
(From Unit 4, Lesson 12.)