Lesson 10

Representing Large Numbers on the Number Line

Let’s visualize large numbers on the number line using powers of 10.

Problem 1

Find three different ways to write the number 437,000 using powers of 10.

Problem 2

For each pair of numbers below, circle the number that is greater. Estimate how many times greater.

  1. \(17 \boldcdot 10^8\) or \(4 \boldcdot 10^8\)
  2. \(2 \boldcdot 10^6\) or \(7.839 \boldcdot 10^6\)
  3. \(42 \boldcdot 10^7\) or \(8.5 \boldcdot 10^8\)

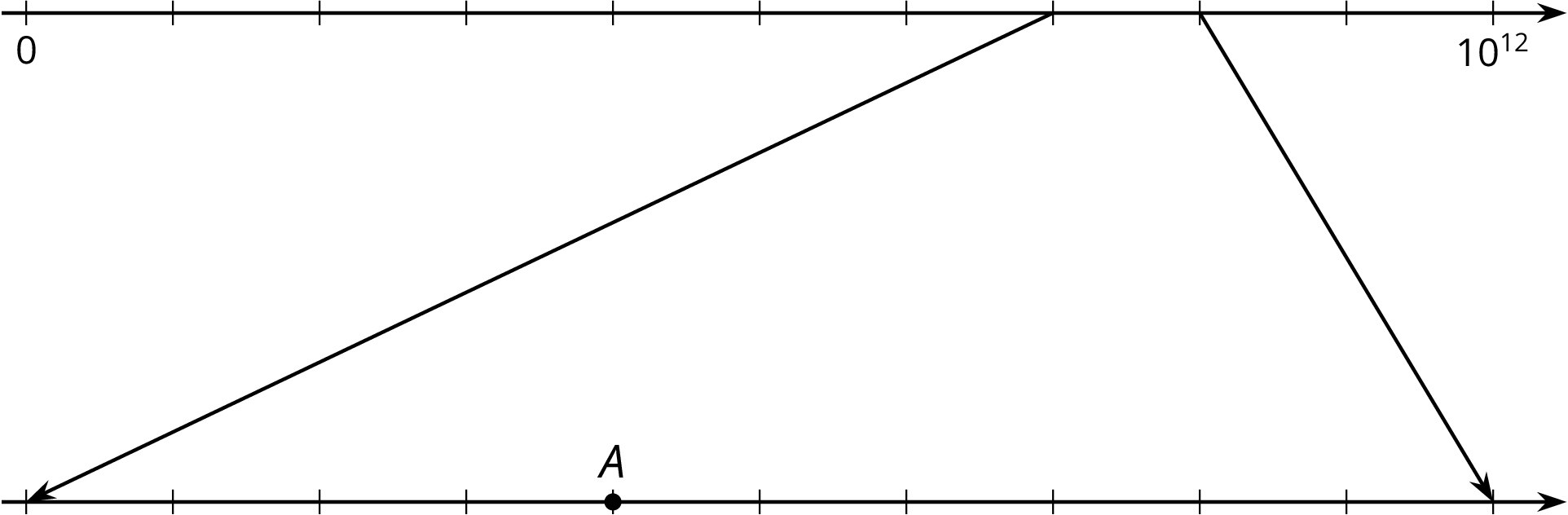
Problem 3

What number is represented by point \(A\)? Explain or show how you know.

A zoomed in number line. Top line, 0 on the first tick mark, 10 to the twelth power on the 11th tick mark.  The eighth & ninth tick marks are zoomed out to show 11 tick marks, the fifth is labeled A.

 

Problem 4

Here is a scatter plot that shows the number of points and assists by a set of hockey players. Select all the following that describe the association in the scatter plot:

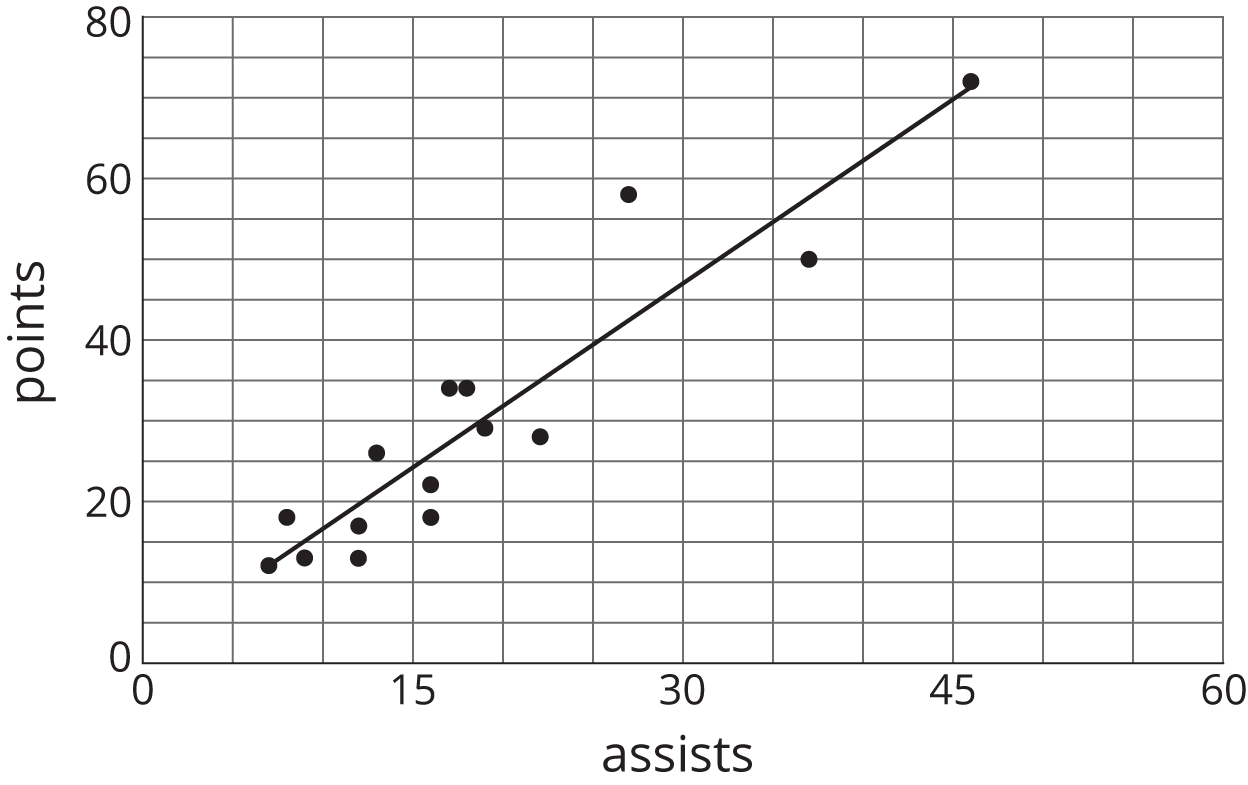
Scatterplot, horizontal, assists, 0 to 60 by 15, vertical, points, 0 to 80 by 20.  A collection of points is clustered around a line through 7 comma 12 and 47 comma 72.

A:

Linear association

B:

Non-linear association

C:

Positive association

D:

Negative association

E:

No association

(From Unit 6, Lesson 7.)

Problem 5

Here is the graph of days and the predicted number of hours of sunlight, \(h\), on the \(d\)-th day of the year. 

Coordinate plane, horizontal, d, 0 to 350 by 50, vertical, h, 0 to 20 by 5. A curve begins at 0 comma 8, increases to 180 comma 18, then decreases to 365 comma 8.


 

  1. Is hours of sunlight a function of days of the year? Explain how you know.

  2. For what days of the year is the number of hours of sunlight increasing? For what days of the year is the number of hours of sunlight decreasing?

  3. Which day of the year has the greatest number of hours of sunlight?

(From Unit 5, Lesson 5.)