Lesson 9
Side Length Quotients in Similar Triangles
Let’s find missing side lengths in triangles.
Problem 1
These two triangles are similar. What are \(a\) and \(b\)? Note: the two figures are not drawn to scale.
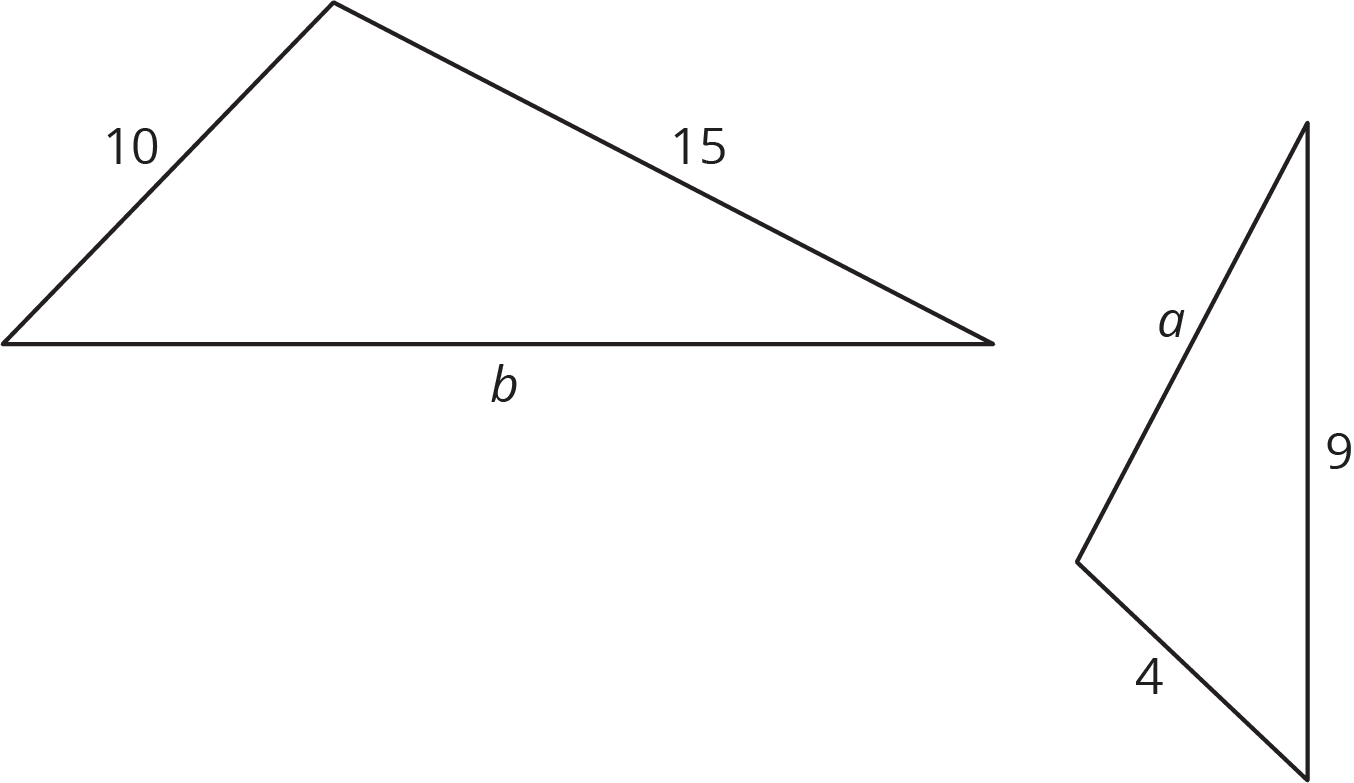
Problem 2
Here is triangle \(ABC\). Triangle \(XYZ\) is similar to \(ABC\) with scale factor \(\frac 1 4\).
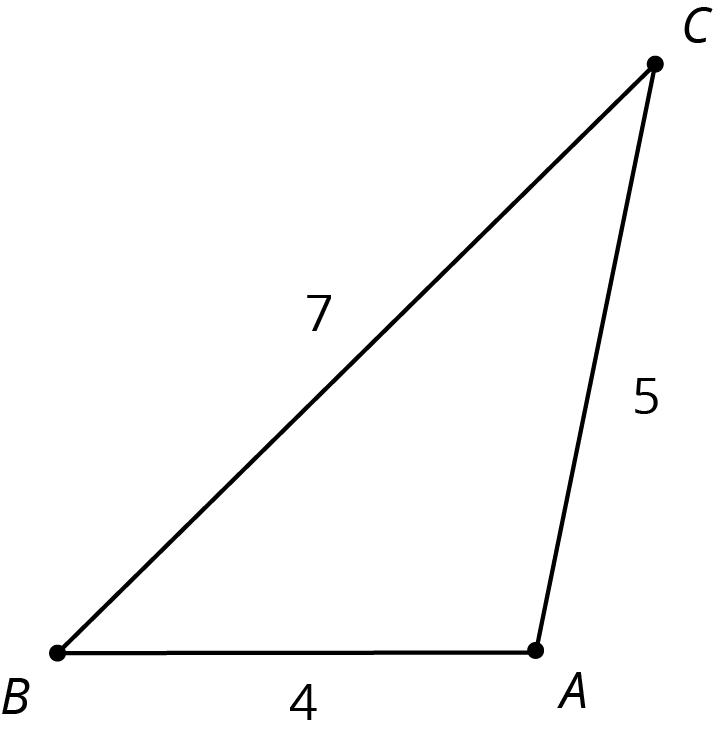
- Draw what triangle \(XYZ\) might look like.
-
How do the angle measures of triangle \(XYZ\) compare to triangle \(ABC\)? Explain how you know.
-
What are the side lengths of triangle \(XYZ\)?
- For triangle \(XYZ\), calculate (long side) \(\div\) (medium side), and compare to triangle \(ABC\).
Problem 3
The two triangles shown are similar. Find the value of \(\frac d c\).
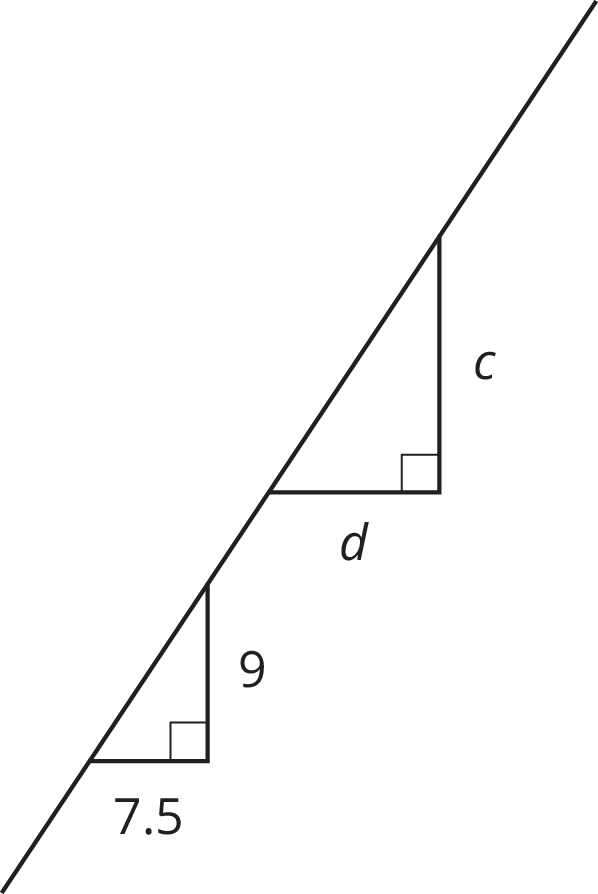
Problem 4
The diagram shows two nested triangles that share a vertex. Find a center and a scale factor for a dilation that would move the larger triangle to the smaller triangle.
