Lesson 10
Meet Slope
Let’s learn about the slope of a line.
10.1: Equal Quotients
Write some numbers that are equal to \(15 \div 12\).
10.2: Similar Triangles on the Same Line
-
The figure shows three right triangles, each with its longest side on the same line. Your teacher will assign you two triangles. Explain why the two triangles are similar.

- Complete the table.
triangle length of
vertical sidelength of
horizontal side(vertical side) \(\div\) (horizontal side) \(ABC\) \(CDE\) \(FGH\)
10.3: Multiple Lines with the Same Slope
- Draw two lines with slope 3. What do you notice about the two lines?
- Draw two lines with slope \(\frac{1}{2}\). What do you notice about the two lines?
As we learn more about lines, we will occasionally have to consider perfectly vertical lines as a special case and treat them differently. Think about applying what you have learned in the last couple of activities to the case of vertical lines. What is the same? What is different?
10.4: Different Slopes of Different Lines
Here are several lines.

- Match each line shown with a slope from this list: \(\frac13\), 2, 1, 0.25, \(\frac32\), \(\frac12\).
- One of the given slopes does not have a line to match. Draw a line with this slope on the empty grid (F).
Summary
Here is a line drawn on a grid. There are also four right triangles drawn. Do you notice anything the triangles have in common?

These four triangles are all examples of slope triangles. One side of a slope triangle is on the line, one side is vertical, and another side is horizontal. The slope of the line is the quotient of the length of the vertical side and the length of the horizontal side of the slope triangle. This number is the same for all slope triangles for the same line because all slope triangles for the same line are similar.
In this example, the slope of the line is \(\frac{2}{3}\), which is what all four triangles have in common. Here is how the slope is calculated using the slope triangles:
- Points \(A\) and \(B\) give \(2\div 3=\frac23\)
- Points \(D\) and \(B\) give \(4\div 6=\frac23\)
- Points \(A\) and \(C\) give \(4\div 6=\frac23\)
- Points \(A\) and \(E\) give \(\frac23 \div 1=\frac23\)
Glossary Entries
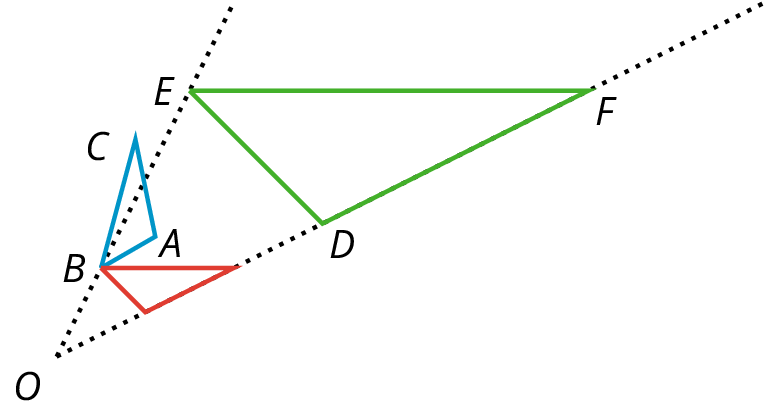
- similar
Two figures are similar if one can fit exactly over the other after rigid transformations and dilations.
In this figure, triangle \(ABC\) is similar to triangle \(DEF\).
If \(ABC\) is rotated around point \(B\) and then dilated with center point \(O\), then it will fit exactly over \(DEF\). This means that they are similar.
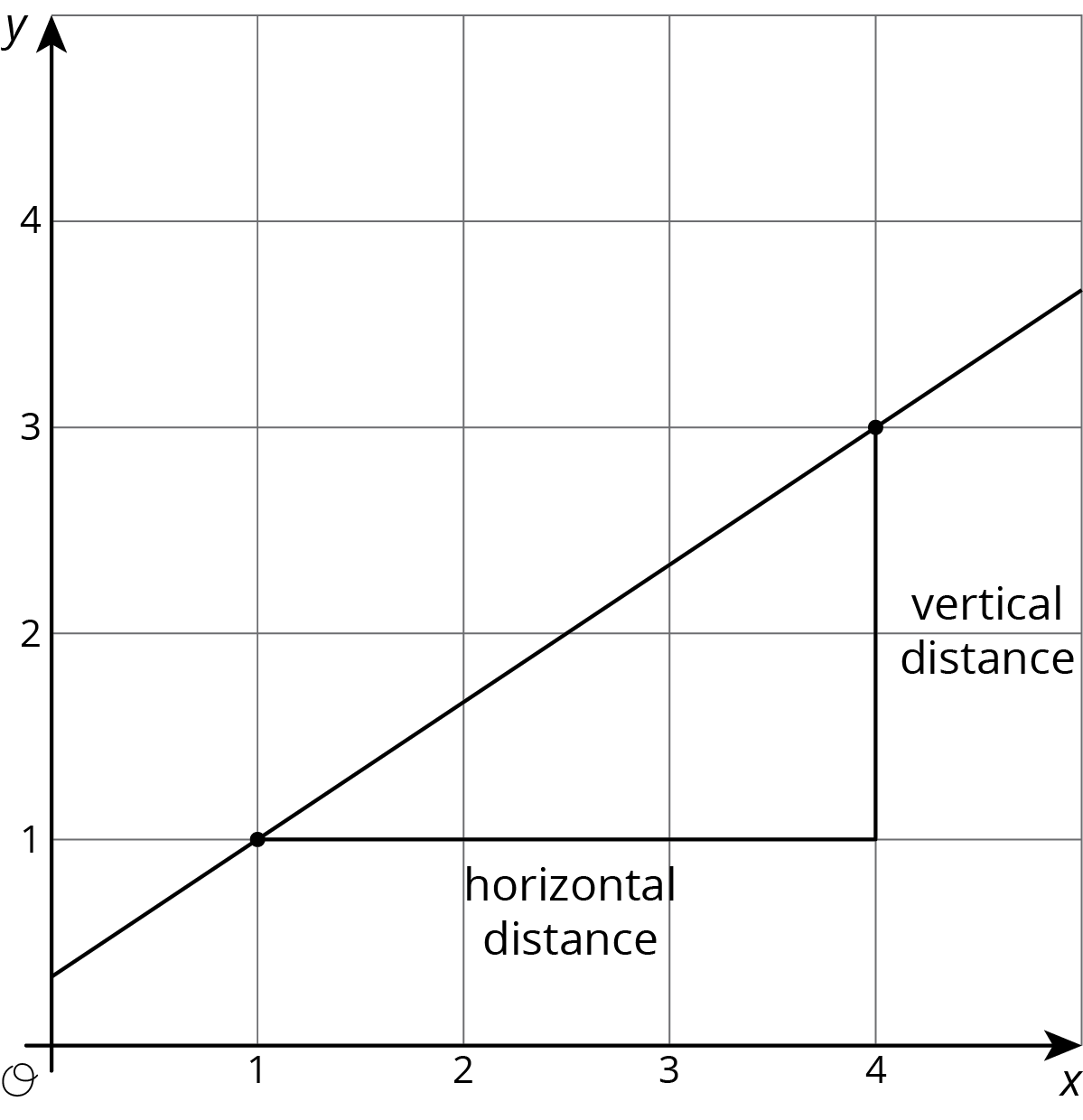
- slope
The slope of a line is a number we can calculate using any two points on the line. To find the slope, divide the vertical distance between the points by the horizontal distance.
The slope of this line is 2 divided by 3 or \(\frac23\).