Lesson 7
Similar Polygons
Let’s look at sides and angles of similar polygons.
Problem 1
Triangle \(DEF\) is a dilation of triangle \(ABC\) with scale factor 2. In triangle \(ABC\), the largest angle measures \(82^\circ\). What is the largest angle measure in triangle \(DEF\)?
\(41^\circ\)
\(82^\circ\)
\(123^\circ\)
\(164^\circ\)
Problem 2
Draw two polygons that are similar but could be mistaken for not being similar. Explain why they are similar.
Problem 3
Draw two polygons that are not similar but could be mistaken for being similar. Explain why they are not similar.
Problem 4
These two triangles are similar. Find side lengths \(a\) and \(b\). Note: the two figures are not drawn to scale.

Problem 5
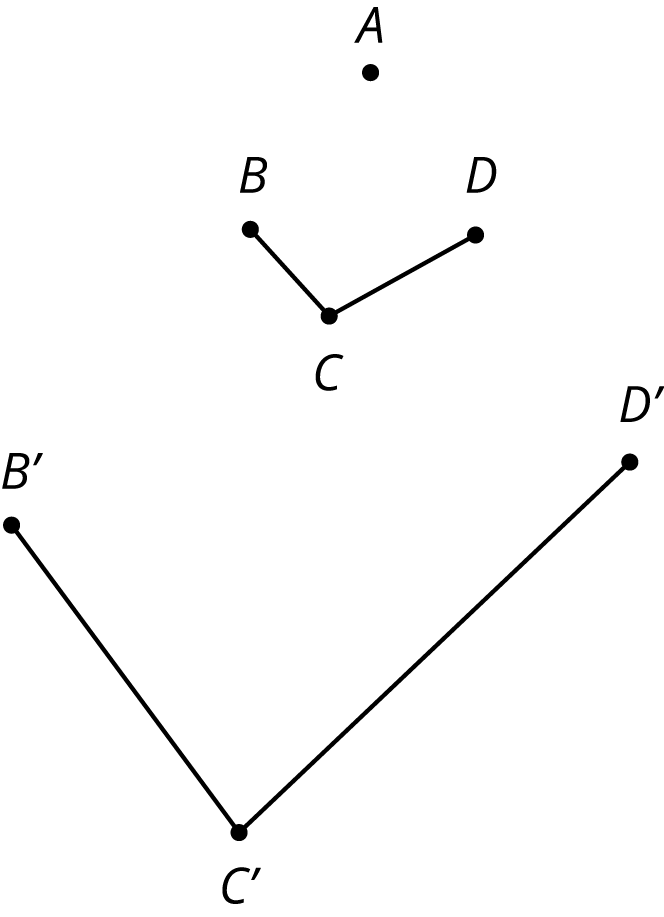
Jada claims that \(B’C’D’\) is a dilation of \(BCD\) using \(A\) as the center of dilation.
What are some ways you can convince Jada that her claim is not true?
Problem 6
-
Draw a horizontal line segment \(AB\).
- Rotate segment \(AB\) \(90^\circ\) counterclockwise around point \(A\). Label any new points.
- Rotate segment \(AB\) \(90^\circ\) clockwise around point \(B\). Label any new points.
- Describe a transformation on segment \(AB\) you could use to finish building a square.