Lesson 2

Circular Grid

Let’s dilate figures on circular grids.

Problem 1

Here are Circles \(c\) and \(d\). Point \(O\) is the center of dilation, and the dilation takes Circle \(c\) to Circle \(d\).

Dilation

 

  1. Plot a point on Circle \(c\). Label the point \(P\). Plot where \(P\) goes when the dilation is applied.
  2. Plot a point on Circle \(d\). Label the point \(Q\). Plot a point that the dilation takes to \(Q\).

Problem 2

Here is triangle \(ABC\).

Triangle A B C and point P on a circular grid. The coordinates of triangle A B C are A(negative 2 comma 2), B(negative 4 comma negative 1) and C(3 comma negative 1) and of point P at P(0 comma 0).
  1. Dilate each vertex of triangle \(ABC\) using \(P\) as the center of dilation and a scale factor of 2. Draw the triangle connecting the three new points.
  2. Dilate each vertex of triangle \(ABC\) using \(P\) as the center of dilation and a scale factor of \(\frac 1 2\). Draw the triangle connecting the three new points.

  3. Measure the longest side of each of the three triangles. What do you notice?

  4. Measure the angles of each triangle. What do you notice?

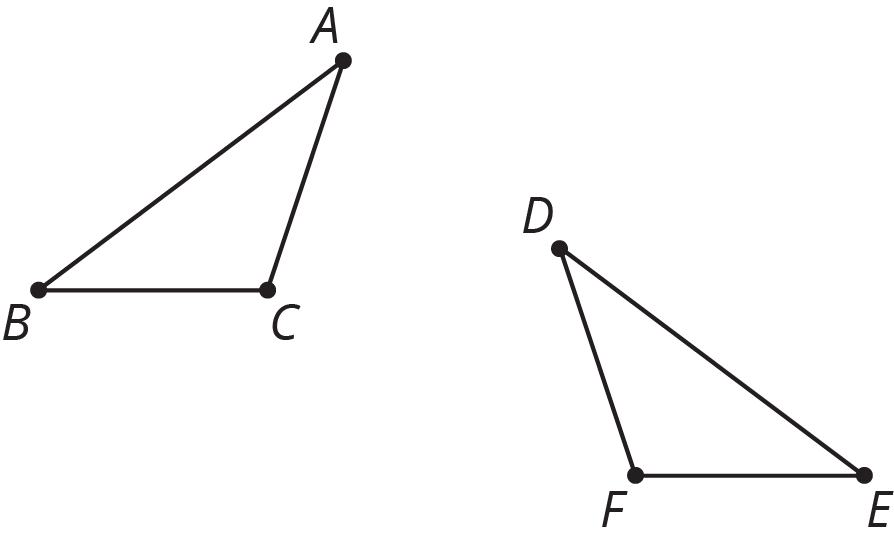
Problem 3

Describe a rigid transformation that you could use to show the polygons are congruent.

Triangles A B C and D E F.

 

(From Unit 1, Lesson 12.)

Problem 4

The line has been partitioned into three angles.

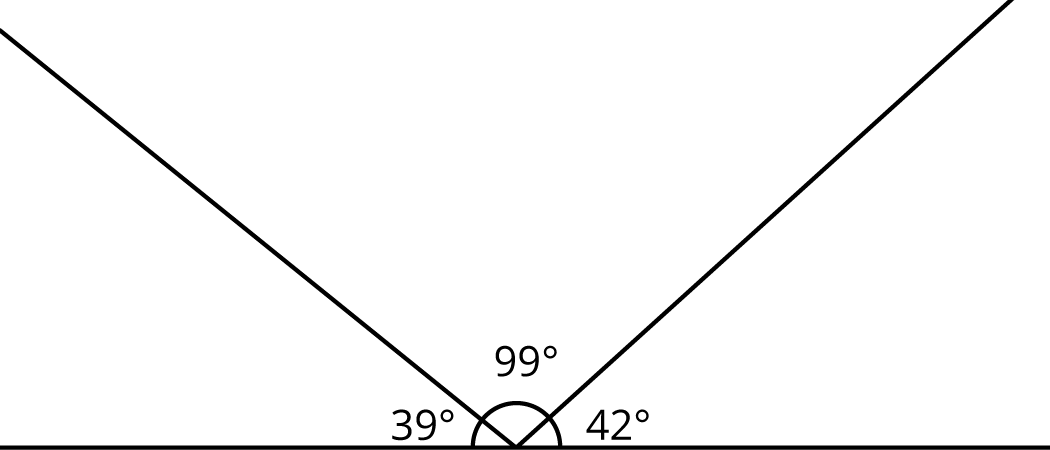
A straight line with two rays coming out of a single point.

Is there a triangle with these three angle measures? Explain.

(From Unit 1, Lesson 15.)