Lesson 10
Meet Slope
Let’s learn about the slope of a line.
Problem 1
Of the three lines in the graph, one has slope 1, one has slope 2, and one has slope \(\frac{1}{5}.\) Label each line with its slope.
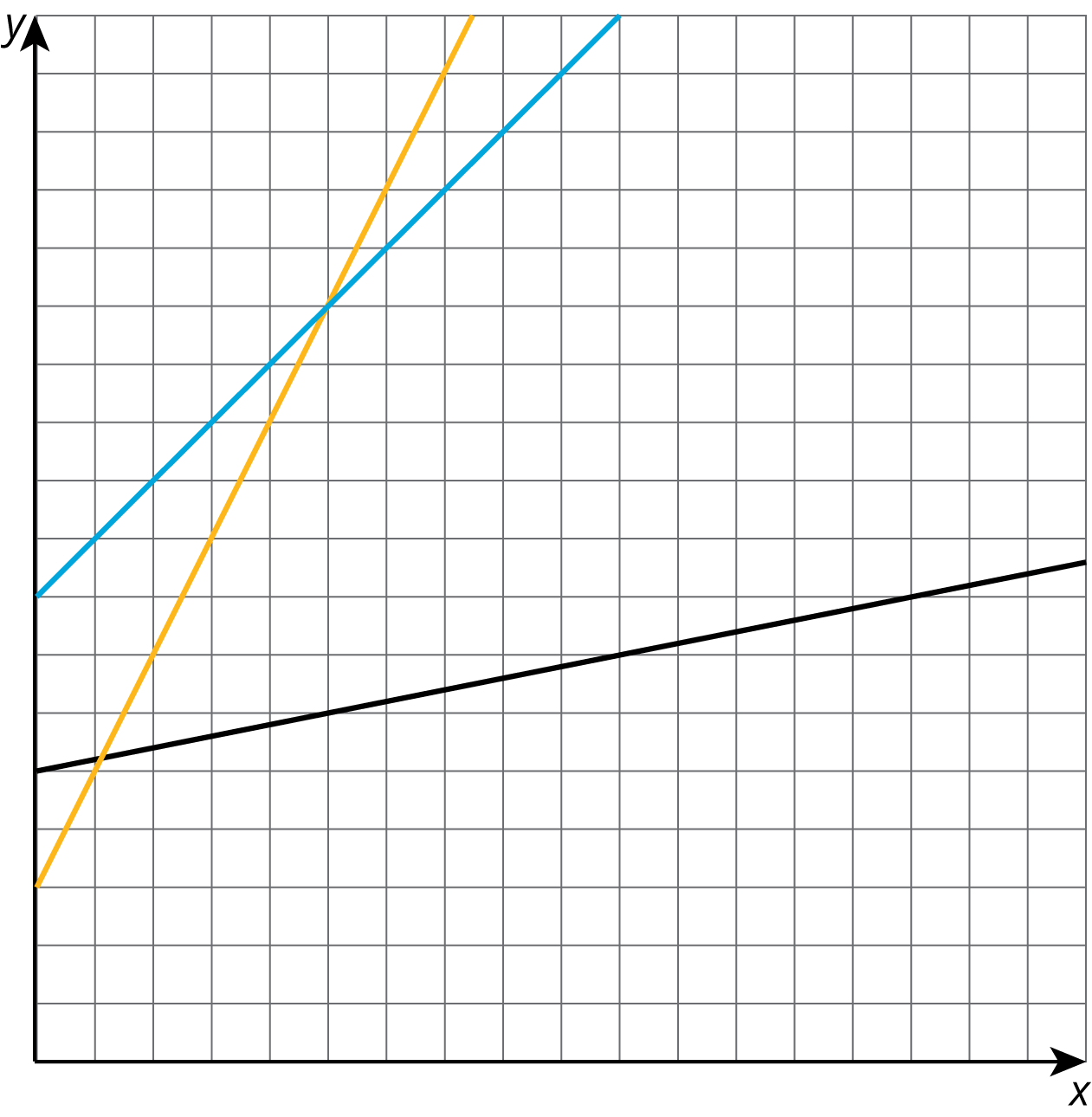
Problem 2
Draw three lines with slope 2, and three lines with slope \(\frac 1 3\). What do you notice?

Problem 3
The figure shows two right triangles, each with its longest side on the same line.

- Explain how you know the two triangles are similar.
- How long is \(XY\)?
- For each triangle, calculate (vertical side) \(\div\) (horizontal side).
- What is the slope of the line? Explain how you know.
Problem 4
Triangle \(A\) has side lengths 3, 4, and 5. Triangle \(B\) has side lengths 6, 7, and 8.
-
Explain how you know that Triangle \(B\) is not similar to Triangle \(A\).
- Give possible side lengths for Triangle \(B\) so that it is similar to Triangle \(A\).