Lesson 11

There is a proportional relationship between the number of months a person has had a streaming movie subscription and the total amount of money they have paid for the subscription. The cost for 6 months is $47.94. The point \((6, 47.94)\) is shown on the graph below.

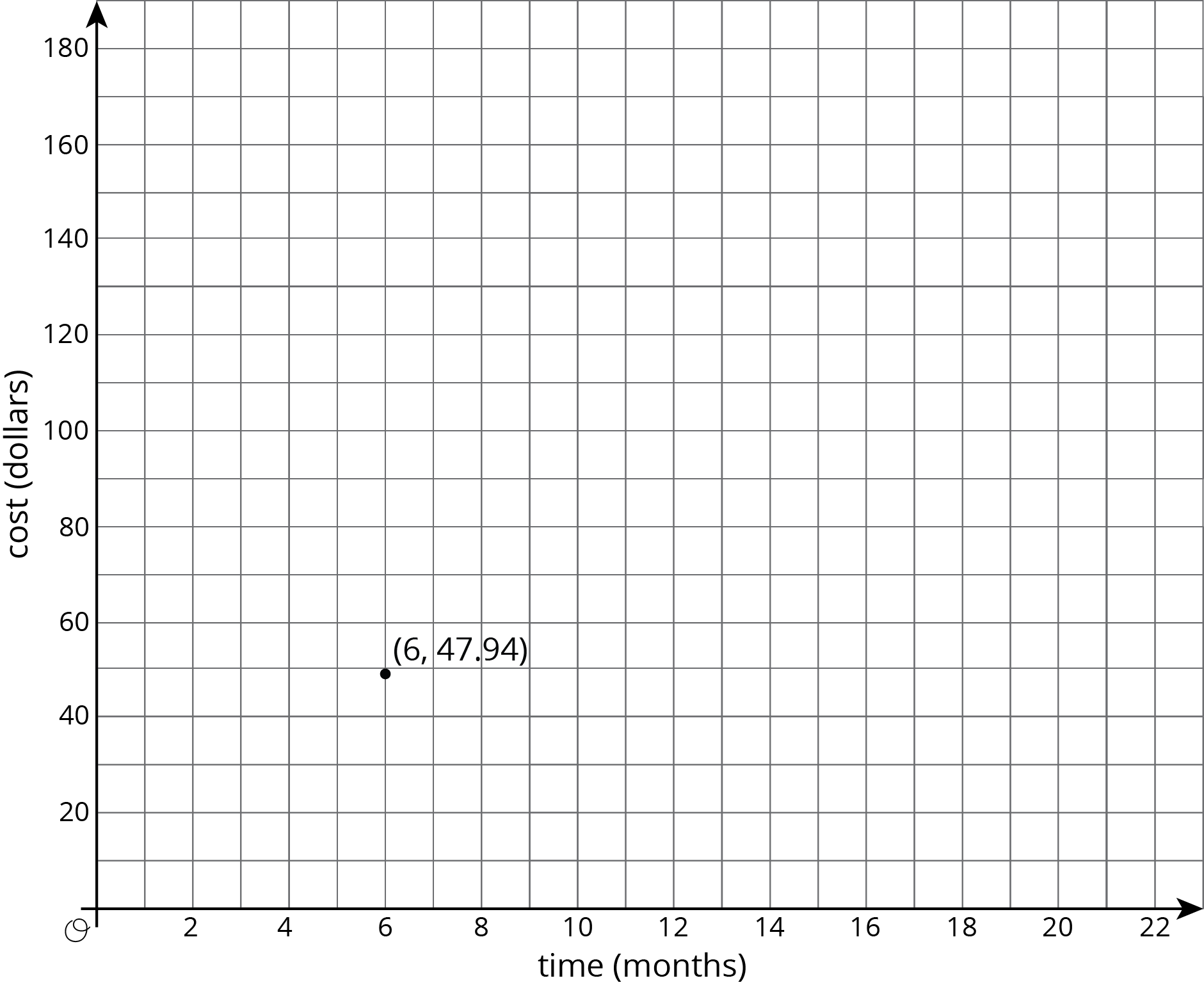
1. What is the constant of proportionality in this relationship?
2. What does the constant of proportionality tell us about the situation?
3. Add at least three more points to the graph and label them with their coordinates.
4. Write an equation that represents the relationship between \(C\), the total cost of the subscription, and \(m\), the number of months.

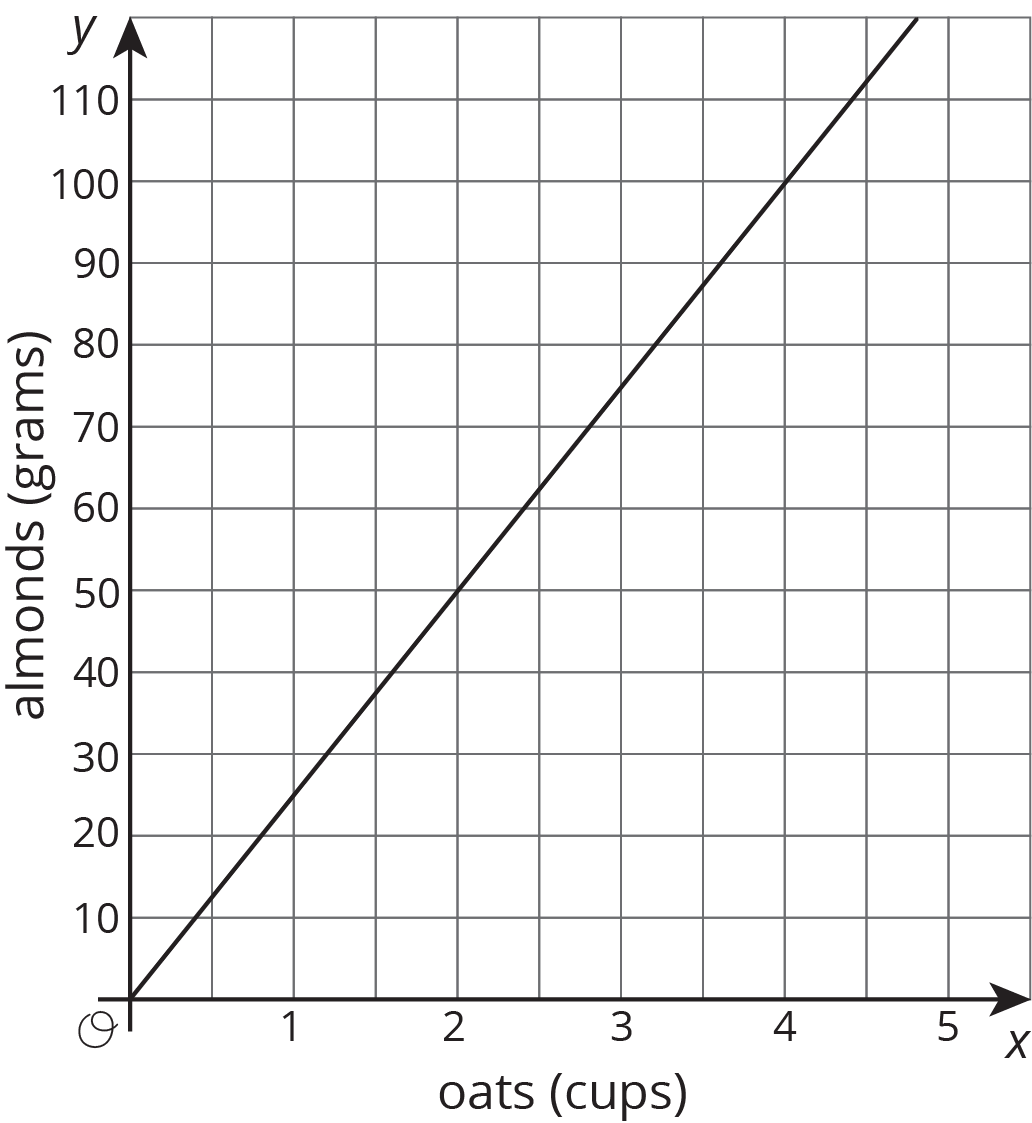
The graph shows the amounts of almonds, in grams, for different amounts of oats, in cups, in a granola mix. Label the point \((1, k)\) on the graph, find the value of \(k\), and explain its meaning.

 

To make a friendship bracelet, some long strings are lined up then taking one string and tying it in a knot with each of the other strings to create a row of knots. A new string is chosen and knotted with the all the other strings to create a second row. This process is repeated until there are enough rows to make a bracelet to fit around your friend's wrist.

Are the number of knots proportional to the number of rows? Explain your reasoning.

What information do you need to know to write an equation relating two quantities that have a proportional relationship?