Lesson 9
The Distributive Property, Part 1
Let's use the distributive property to make calculating easier.
Problem 1
Select all the expressions that represent the area of the large, outer rectangle.
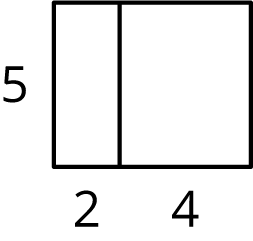
\(5(2+4)\)
\(5 \boldcdot 2 + 4\)
\(5 \boldcdot 2 + 5 \boldcdot 4\)
\(5 \boldcdot 2 \boldcdot 4\)
\(5 + 2+ 4\)
\(5 \boldcdot 6\)
Problem 2
Draw and label diagrams that show these two methods for calculating \(19 \boldcdot 50\).
- First find \(10\boldcdot 50\) and then add \(9 \boldcdot 50\).
-
First find \(20 \boldcdot 50\) and then take away 50.
Problem 3
Complete each calculation using the distributive property.
\(\displaystyle 98 \boldcdot 24\) \(\displaystyle (100-2) \boldcdot 24\) \(\displaystyle \ldots\)
\(\displaystyle 21 \boldcdot 15\) \(\displaystyle (20 + 1) \boldcdot 15\) \(\displaystyle \ldots\)
\(\displaystyle 0.51 \boldcdot 40\) \(\displaystyle (0.5 + 0.01) \boldcdot 40\) \(\displaystyle \ldots\)
Problem 4
A group of 8 friends go to the movies. A bag of popcorn costs $2.99. How much will it cost to get one bag of popcorn for each friend? Explain how you can calculate this amount mentally.
Problem 5
- On graph paper, draw diagrams of \(a+a+a+a\) and \(4a\) when \(a\) is 1, 2, and 3. What do you notice?
- Do \(a+a+a+a\) and \(4a\) have the same value for any value of \(a\)? Explain how you know.
Problem 6
120% of \(x\) is equal to 78.
- Write an equation that shows the relationship of 120%, \(x\), and 78.
- Use your equation to find \(x\). Show your reasoning.
Problem 7
Kiran’s aunt is 17 years older than Kiran.
-
How old will Kiran’s aunt be when Kiran is:
15 years old?
30 years old?
\(x\) years old?
- How old will Kiran be when his aunt is 60 years old?