Lesson 3
Staying in Balance
Let's use balanced hangers to help us solve equations.
Problem 1
Select all the equations that represent the hanger.
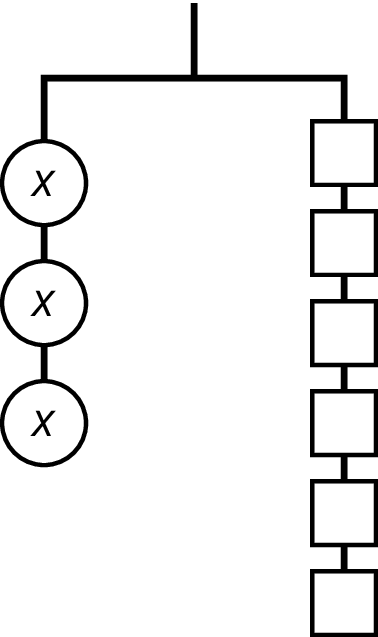
\(x+x+x = 1+1+1+1+1+1\)
\(x \boldcdot x \boldcdot x = 6\)
\(3x = 6\)
\(x + 3 = 6\)
\(x \boldcdot x \boldcdot x = 1 \boldcdot 1 \boldcdot 1 \boldcdot 1 \boldcdot 1 \boldcdot 1\)
Problem 2
Write an equation to represent each hanger.
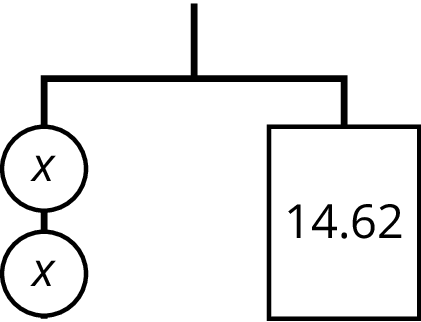
Problem 3
- Write an equation to represent the hanger.
- Explain how to reason with the hanger to find the value of \(x\).
- Explain how to reason with the equation to find the value of \(x\).
Problem 4
Andre says that \(x\) is 7 because he can move the two 1s with the \(x\) to the other side.
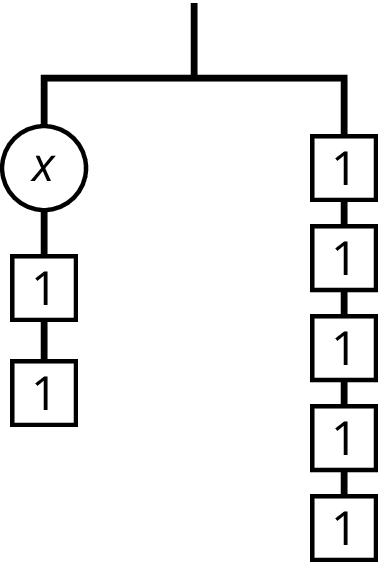
Do you agree with Andre? Explain your reasoning.
Problem 5
Match each equation to one of the diagrams.
- \(12-m=4\)
- \(12=4\boldcdot m\)
- \(m-4=12\)
- \(\frac{m}{4}=12\)

Problem 6
The area of a rectangle is 14 square units. It has side lengths \(x\) and \(y\). Given each value for \(x\), find \(y\).
- \(x=2\frac13\)
- \(x=4\frac15\)
- \(x=\frac76\)
Problem 7
Lin needs to save up $20 for a new game. How much money does she have if she has saved each percentage of her goal. Explain your reasoning.
- 25%
- 75%
- 125%