Lesson 15
Equivalent Exponential Expressions
Let's investigate expressions with variables and exponents.
Problem 1
Evaluate each expression if \(x=3\).
- \(2^x\)
- \(x^2\)
- \(1^x\)
- \(x^1\)
- \(\left(\frac12\right)^x\)
Problem 2
Evaluate each expression for the given value of each variable.
-
\(2 + x^3\), \(x\) is 3
-
\(x^2\), \(x\) is \(\frac{1}{2}\)
-
\(3x^2+y\), \(x\) is 5 \(y\) is 3
-
\(10y + x^2\), \(x\) is 6 \(y\) is 4
Problem 3
Decide if the expressions have the same value. If not, determine which expression has the larger value.
-
\(2^3\) and \(3^2\)
-
\(1^{31}\) and \(31^1\)
-
\(4^2\) and \(2^4\)
- \(\left(\frac12\right)^3\) and \(\left(\frac13\right)^2\)
Problem 4
Match each equation to its solution.
Problem 5
An adult pass at the amusement park costs 1.6 times as much as a child’s pass.
-
How many dollars does an adult pass cost if a child’s pass costs:
$5?
$10?
\(w\) dollars?
- A child’s pass costs $15. How many dollars does an adult pass cost?
Problem 6
Jada reads 5 pages every 20 minutes. At this rate, how many pages can she read in 1 hour?
-
Use a double number line to find the answer.
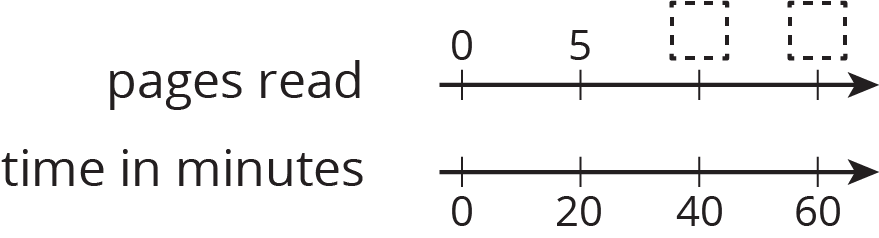
- Use a table to find the answer.
| pages read |
time in minutes |
|---|---|
| 5 | 20 |
Which strategy do you think is better, and why?