Lesson 12

Meaning of Exponents

Let’s see how exponents show repeated multiplication.

Problem 1

Select all the expressions that are equivalent to 64.

A:

\(2^6\)

B:

\(2^8\)

C:

\(4^3\)

D:

\(8^2\)

E:

\(16^4\)

F:

\(32^2\)

Problem 2

Select all the expressions that equal \(3^4\).

A:

7

B:

\(4^3\)

C:

12

D:

81

E:

64

F:

\(9^2\)

Problem 3

\(4^5\) is equal to 1,024. Evaluate each expression.

  1. \(4^6\)

  2. \(4^4\)

  3. \(4^3\boldcdot  4^2\)

Problem 4

\(6^3=216\). Using exponents, write three more expressions whose value is 216.

Problem 5

Find two different ways to rewrite \(3xy + 6yz\) using the distributive property.

(From Unit 6, Lesson 11.)

Problem 6

Solve each equation.

\(a - 2.01 = 5.5\)

 

\(b + 2.01 = 5.5\)

\(10c = 13.71\)

 

\(100d = 13.71\)

(From Unit 6, Lesson 5.)

Problem 7

Which expressions represent the total area of the large rectangle? Select all that apply.

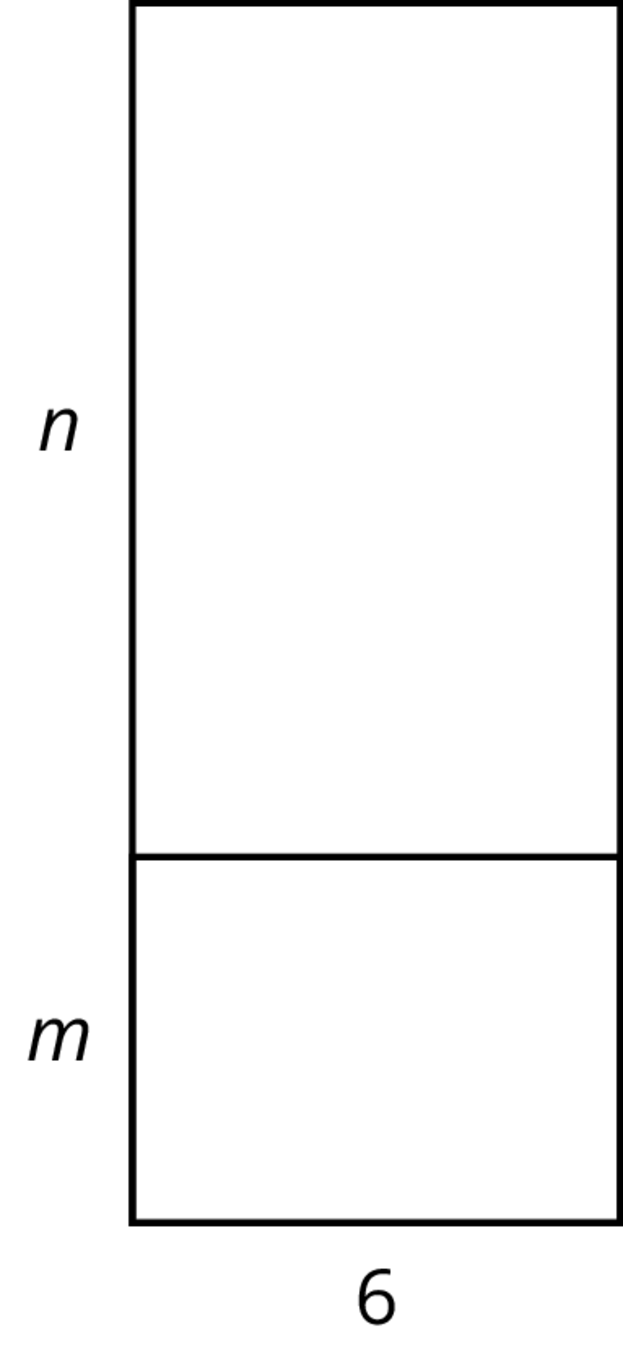
A rectangle partitioned by a horizontal line segment into two smaller rectangles. The bottom horizontal is labeled 6 and the vertical side lengths are labeled n and m.

​​

A:

\(6(m+n)\)

B:

\(6n + m\)

C:

\(6n + 6m\)

D:

\(6mn\)

E:

\((n+m)6\)

(From Unit 6, Lesson 10.)

Problem 8

Is each statement true or false? Explain your reasoning.

  1. \(\frac{45}{100} \boldcdot 72 = \frac{45}{72} \boldcdot 100\)
  2. 16% of 250 is equal to 250% of 16
(From Unit 3, Lesson 16.)