Lesson 10

Dividing by Unit and Non-Unit Fractions

Let’s look for patterns when we divide by a fraction.

Problem 1

Priya is sharing 24 apples equally with some friends. She uses division to determine how many people can have a share if each person gets a particular number of apples. For example, \(24 \div 4 = 6\) means that if each person gets 4 apples, then 6 people can have apples. Here are some other calculations:

\(24 \div 4 = 6\)

\(24 \div 2 = 12\)

\(24 \div 1 = 24\)

\(24 \div \frac12 = {?}\)

  1. Priya thinks the “?” represents a number less than 24. Do you agree? Explain or show your reasoning.

  2. In the case of \(24 \div \frac12 = {?}\), how many people can have apples?

Problem 2

Here is a centimeter ruler.

  1. Use the ruler to find \(1 \div \frac{1}{10}\) and \(4 \div \frac{1}{10}\).

  2. What calculation did you do each time?

  3. Use this pattern to find \(18 \div \frac{1}{10}\).

  4. Explain how you could find \(4\div \frac{2}{10}\) and \(4\div \frac{8}{10}\).
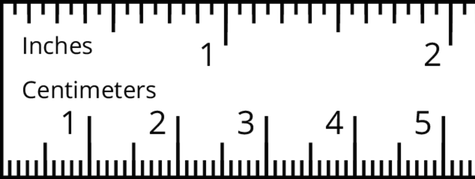
A centimeter ruler. 

Problem 3

Find each quotient.

  1. \(5 \div \frac{1}{10}\)
  2. \(5 \div \frac{3}{10}\)
  3. \(5\div \frac{9}{10}\)

Problem 4

Use the fact that \(2\frac12 \div \frac18=20\) to find \(2\frac12 \div \frac58\). Explain or show your reasoning.

Problem 5

Consider the problem: It takes one week for a crew of workers to pave \(\frac35\) kilometer of a road. At that rate, how long will it take to pave 1 kilometer?

Write a multiplication equation and a division equation to represent the question. Then find the answer and show your reasoning.

(From Unit 4, Lesson 9.)

Problem 6

A box contains \(1\frac 34\) pounds of pancake mix. Jada used \(\frac 78\) pound for a recipe. What fraction of the pancake mix in the box did she use? Explain or show your reasoning. Draw a diagram, if needed.

(From Unit 4, Lesson 7.)

Problem 7

Calculate each percentage mentally.

  1. 25% of 400
  2. 50% of 90
  1. 75% of 200
  2. 10% of 8,000
  1. 5% of 20
(From Unit 3, Lesson 14.)