Lesson 6
Using Diagrams to Find the Number of Groups
Let’s draw tape diagrams to think about division with fractions.
6.1: How Many of These in That?
- We can think of the division expression \(10 \div 2\frac12\) as the question: “How many groups of \(2\frac 12\) are in 10?” Complete the tape diagram to represent this question. Then find the answer.

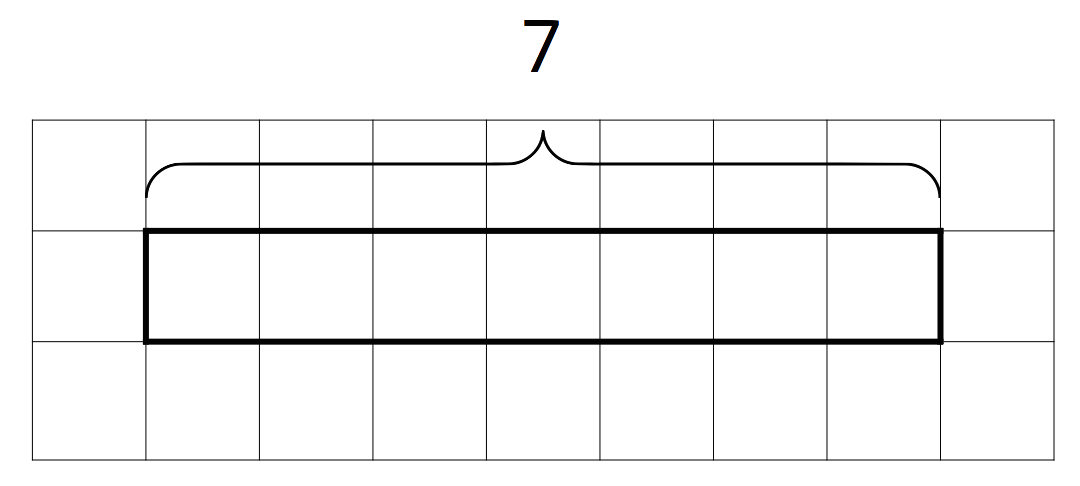
- Complete the tape diagram to represent the question: “How many groups of 2 are in 7?” Then find the answer.
6.2: Representing Groups of Fractions with Tape Diagrams
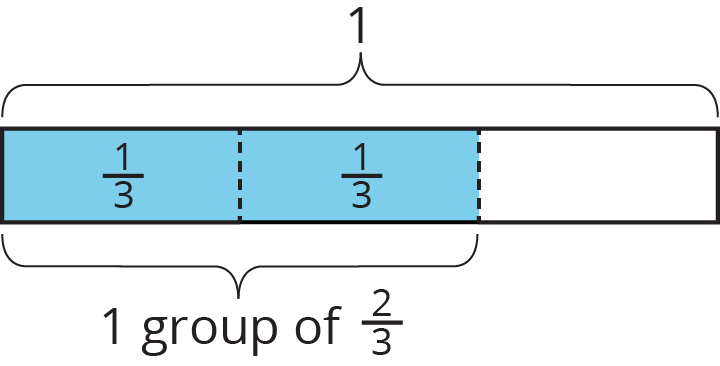
To make sense of the question “How many \(\frac 23\)s are in 1?,” Andre wrote equations and drew a tape diagram.
\(\displaystyle {?} \boldcdot \frac 23 = 1\)
\(\displaystyle 1 \div \frac 23 = {?}\)
-
In an earlier task, we used pattern blocks to help us solve the equation \(1 \div \frac 23 = {?}\). Explain how Andre’s tape diagram can also help us solve the equation.
-
Write a multiplication equation and a division equation for each question. Then, draw a tape diagram and find the answer.
- How many \(\frac 34\)s are in 1?

- How many \(\frac23\)s are in 3?

- How many \(\frac32\)s are in 5?

- How many \(\frac 34\)s are in 1?
6.3: Finding Number of Groups
-
Write a multiplication equation or a division equation for each question. Then, find the answer and explain or show your reasoning.
-
How many \(\frac38\)-inch thick books make a stack that is 6 inches tall?
-
How many groups of \(\frac12\) pound are in \(2\frac 34\) pounds?
-
- Write a question that can be represented by the division equation \(5 \div 1\frac12 = {?}\). Then, find the answer and explain or show your reasoning.
Summary
A baker used 2 kilograms of flour to make several batches of a pastry recipe. The recipe called for \(\frac25\) kilogram of flour per batch. How many batches did she make?
We can think of the question as: “How many groups of \(\frac25\) kilogram make 2 kilograms?” and represent that question with the equations:
\(\displaystyle {?} \boldcdot \frac25=2\)
\(\displaystyle 2 \div \frac25 = {?}\)
To help us make sense of the question, we can draw a tape diagram. This diagram shows 2 whole kilograms, with each kilogram partitioned into fifths.

We can see there are 5 groups of \(\frac 25\) in 2. Multiplying 5 and \(\frac25\) allows us to check this answer: \(5 \boldcdot \frac 25 = \frac{10}{5}\) and \(\frac {10}{5} = 2\), so the answer is correct.
Notice the number of groups that result from \(2 \div \frac25\) is a whole number. Sometimes the number of groups we find from dividing may not be a whole number. Here is an example:
Suppose one serving of rice is \(\frac34\) cup. How many servings are there in \(3\frac12\) cups?
\(\displaystyle {?}\boldcdot \frac34 = 3\frac12\)
\(\displaystyle 3\frac12 \div \frac34 = {?}\)
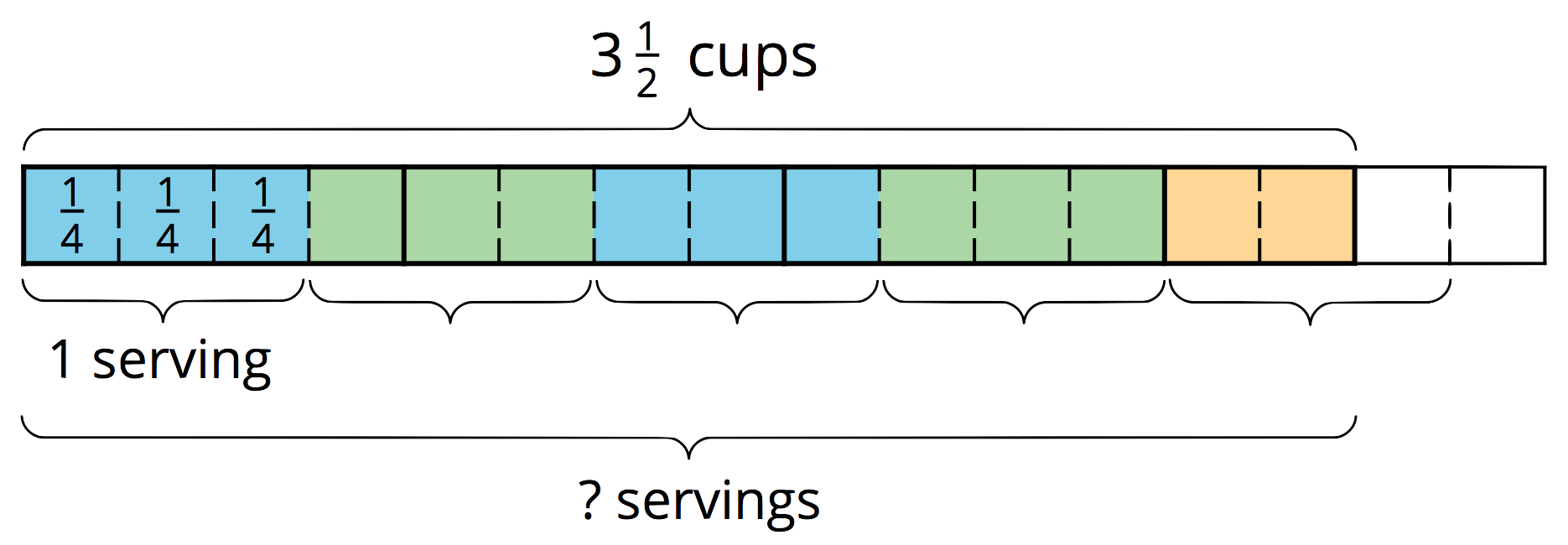
Looking at the diagram, we can see there are 4 full groups of \(\frac 34\), plus 2 fourths. If 3 fourths make a whole group, then 2 fourths make \(\frac 23\) of a group. So the number of servings (the “?” in each equation) is \(4\frac23\). We can check this by multiplying \(4\frac23\) and \(\frac34\).
\(4\frac23 \boldcdot \frac34 = \frac{14}{3} \boldcdot \frac34\), and \(\frac{14}{3} \boldcdot \frac34 = \frac{14}{4}\), which is indeed equivalent to \(3\frac12\).