Lesson 3

Recipes

Let’s explore how ratios affect the way a recipe tastes.

3.1: Flower Pattern

This flower is made up of yellow hexagons, red trapezoids, and green triangles.

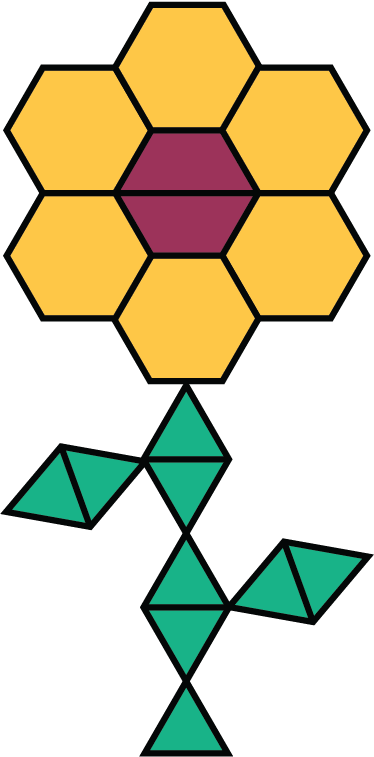
A figure that contains 6 yellow hexagons, 2 red trapezoids, and 9 green triangles.
  1. Write sentences to describe the ratios of the shapes that make up this pattern.
  2. How many of each shape would be in two copies of this flower pattern?

 

3.2: Powdered Drink Mix

Here are diagrams representing three mixtures of powdered drink mix and water:

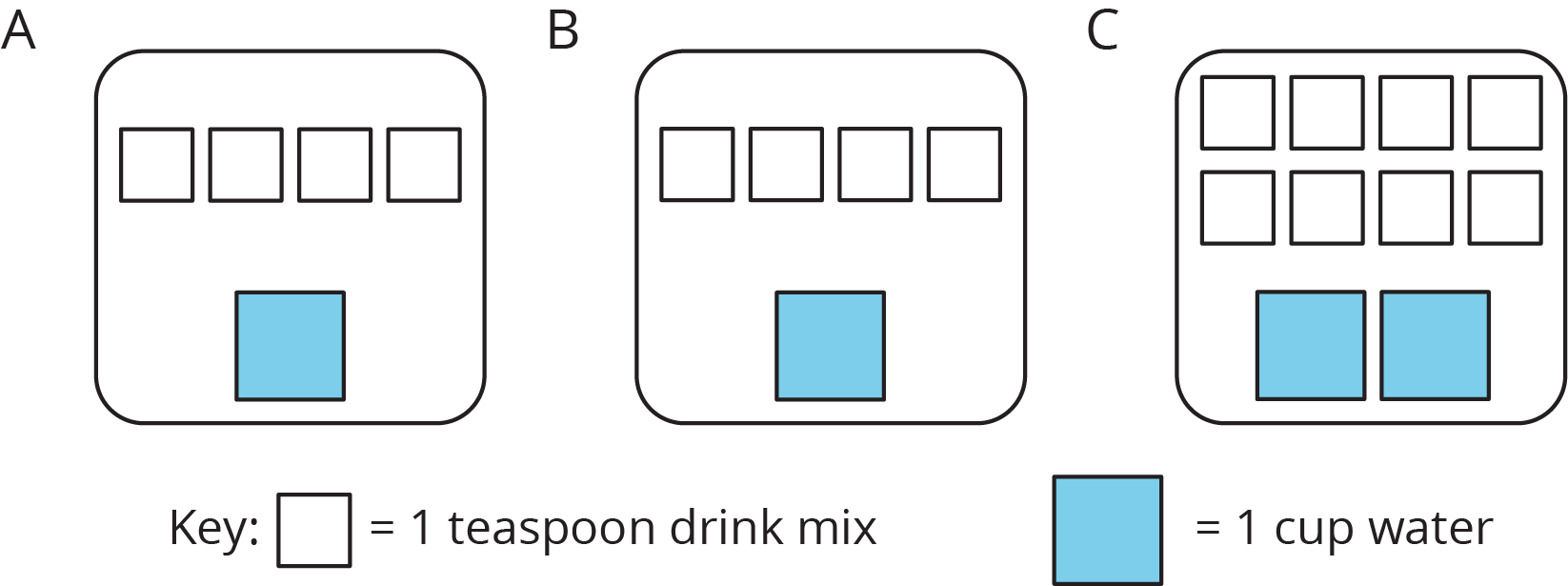
A discrete diagram for three quantities.

  1. How would the taste of Mixture A compare to the taste of Mixture B?

  2. Use the diagrams to complete each statement:

    1. Mixture B uses ______ cups of water and ______ teaspoons of drink mix. The ratio of cups of water to teaspoons of drink mix in Mixture B is ________.

    2. Mixture C uses ______ cups of water and ______ teaspoons of drink mix. The ratio of cups of water to teaspoons of drink mix in Mixture C is ________.

  3. How would the taste of Mixture B compare to the taste of Mixture C?


Sports drinks use sodium (better known as salt) to help people replenish electrolytes. Here are the nutrition labels of two sports drinks.

Two nutrition Labels. Drink A. Drink B.
  1. Which of these drinks is saltier? Explain how you know.
  2. If you wanted to make sure a sports drink was less salty than both of the ones given, what ratio of sodium to water would you use?

3.3: Batches of Cookies

A recipe for one batch of cookies calls for 5 cups of flour and 2 teaspoons of vanilla.

  1. Draw a diagram that shows the amount of flour and vanilla needed for two batches of cookies.

  2. How many batches can you make with 15 cups of flour and 6 teaspoons of vanilla? Show the additional batches by adding more ingredients to your diagram.
  3. How much flour and vanilla would you need for 5 batches of cookies?

  4. Whether the ratio of cups of flour to teaspoons of vanilla is \(5:2\), \(10:4\), or \(15:6\), the recipes would make cookies that taste the same. We call these equivalent ratios.

    1. Find another ratio of cups of flour to teaspoons of vanilla that is equivalent to these ratios.

    2. How many batches can you make using this new ratio of ingredients?

Summary

A recipe for fizzy juice says, “Mix 5 cups of cranberry juice with 2 cups of soda water.”

To double this recipe, we would use 10 cups of cranberry juice with 4 cups of soda water. To triple this recipe, we would use 15 cups of cranberry juice with 6 cups of soda water.

This diagram shows a single batch of the recipe, a double batch, and a triple batch:

Equivalent ratios of a recipe for fizzy juice.

We say that the ratios \(5 : 2\), \(10 : 4\), and \(15 : 6\) are equivalent. Even though the amounts of each ingredient within a single, double, or triple batch are not the same, they would make fizzy juice that tastes the same.