Lesson 14

Percent Increase and Decrease

These materials, when encountered before Algebra 1, Unit 5, Lesson 14 support success in that lesson.

View Student Lesson

14.1: Visualizing Percent Change (10 minutes)

CCSS Standards


Addressing

Routines and Materials


Instructional Routines

Warm-up

The purpose of this activity is for students to understand that a percent increase of 25% corresponds to 125% of the original amount, and a percent decrease of 25% corresponds to 75% of the original amount. Students may be familiar with tape diagrams from earlier grades. This activity reminds students how tape diagrams show relative quantities, and illustrates how they can show percent change.

Launch

Display this image for all to see. Give students 1 minute of quiet think time and ask them to be prepared to share at least one thing they notice and one thing they wonder. Give students another minute to discuss their observations and questions.

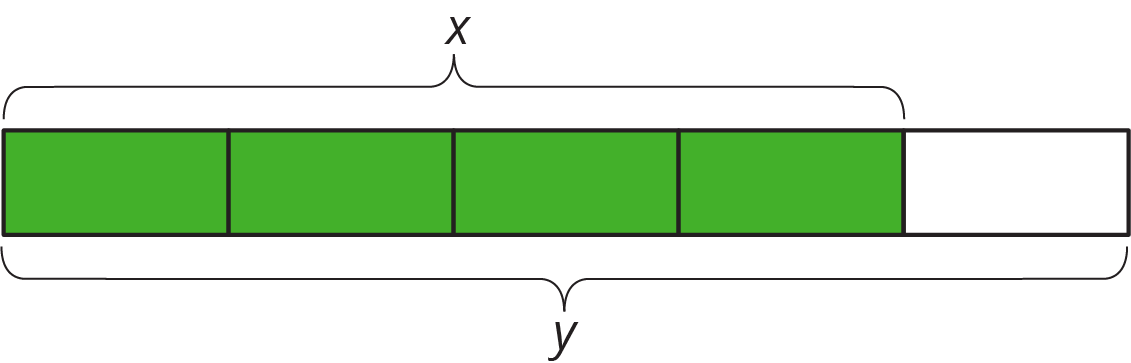
Tape diagram, 5 equal parts. 4 parts, x. Total, y.

Students may notice:

  • There is a tape diagram subdivided into 5 equal intervals.
  • Four of the intervals are shaded, and labeled \(x\).
  • One of the intervals is not shaded.
  • The length of the entire tape diagram is labeled \(y\).
  • \(\frac45\) of the tape diagram is shaded.

Students may wonder:

  • What does the diagram represent?
  • What do \(x\) and \(y\) represent?
  • If the diagram represents a fraction or a percentage, which part is the “whole”?
  • Why are only some of the intervals shaded?

Student Facing

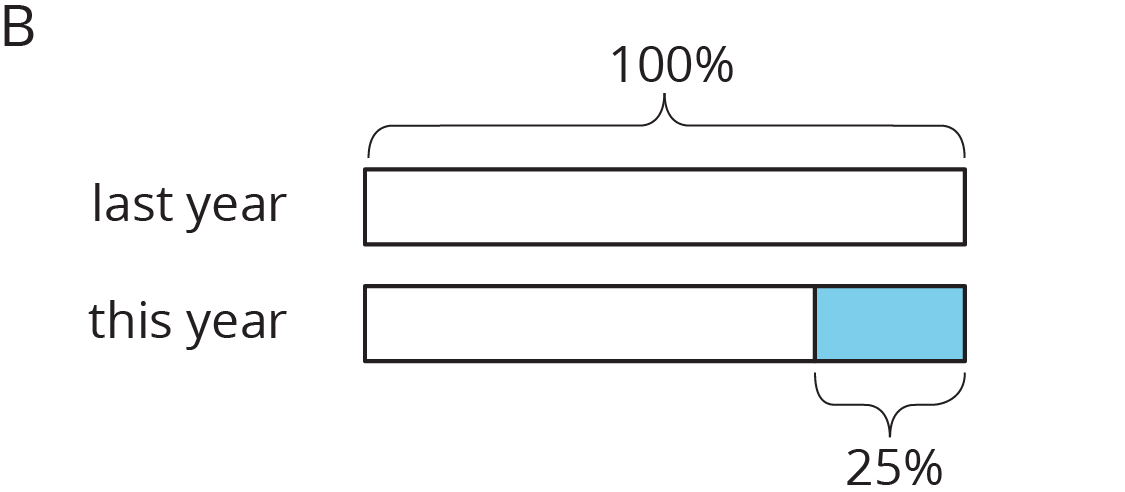
Two tape diagrams. Last year, labeled 100 percent, one long section. This year, with a smaller blue section labeled 25 percent that extends past the 100 percent tape.

Two tape diagrams. Last year, labeled 100 percent, one long section. This year, with a smaller blue section labeled 25 percent.

  1. Match each situation to a diagram. Be prepared to explain your reasoning.
    1. Compared with last year’s student population, this year’s student population increased 25%.
    2. This year’s student population is 75% of last year’s.
    3. Compared with last year, this year’s student population decreased 25%.
    4. This year’s student population is 125% of last year’s student population.
  2. Draw a diagram to represent these situations.
    1. The number of ducks living at the pond increased by 50%.
    2. The number of mosquitoes decreased by 20%.

Student Response

For access, consult one of our IM Certified Partners.

Activity Synthesis

Share the correct matches and ensure everyone understands how the given diagrams are connected to the descriptions. Then, ask students to share their diagrams of the second question and explain their thinking. Here are some questions for discussion:

  • “The ducks increased by 50%. That means the new number of ducks is what percentage of the old number?” (150%)
  • “The mosquitoes decreased by 20%. That means the new number of mosquitoes is what percentage of the old number?” (80%)

14.2: Computing Percent Change Efficiently (15 minutes)

CCSS Standards


Addressing

Activity

In the Algebra 1 lessons, students will need to be able to express a quantity that changes by a given percentage repeatedly. For example, a credit card has a $100 balance, and is charged 12% interest each year. How much do you owe after 5 years? An expression representing the new balance is \(100 \boldcdot (1.12)^5\). In order for this to make sense, they first need to express the result of a percent increase or decrease using only multiplication. This activity helps to build that capacity. Recognizing that the distributive property can be used to rewrite an expression is an example of noticing and making use of structure (MP7).

Launch

Tell students that in this activity, they’ll be learning or revisiting a way to calculate a problem like “\(x\) increases or decreases by a certain percentage. What is the new amount?” You could calculate the percentage of the old amount and add or subtract it from the original amount, but for the upcoming work in Algebra 1, it will be necessary to do this calculation with just one operation.

Give students a few minutes of quiet think time to think about the first question, then select students to share their justification for each step. Ensure students see why each step works before continuing with the rest of the activity. If students get stuck, encourage them to draw a tape diagram.

Provide access to calculators as needed, but note that students don’t need to perform very difficult computations in this activity, since they are just writing equivalent expressions.

Student Facing

An article in the paper says that the local high school’s student population will increase by 10% next year. Diego knows that this year, about 1,300 students attend the high school, and he wants to figure out next year’s population. First, he draws this diagram.

Diagram. 1300 = 100%.1300 and unknown number = 110%.
Here is his work:

  • \(1,\!300 + 0.1(1,\!300)\)
  • \(1,\!300(1 + 0.1)\)
  • \(1,\!300(1.1)\)
  • Multiplying 1,300 by 1.1, he gets 1,430.
  1. Explain each step in Diego’s method. Why does it work?
  2. Use Diego’s method to rewrite each expression so that it only uses multiplication:
    1. \(7 + 0.4 \boldcdot 7\)
    2. \(24 + 0.08 \boldcdot 24\)
    3. \(13 - 0.1 \boldcdot 13\)
    4. \(98 + 98 \boldcdot 0.02\)
  3. The first calculation gives 7 increased by 40%. What do the other calculations give, as a percent change?

Student Response

For access, consult one of our IM Certified Partners.

Activity Synthesis

Invite students to share their solutions. If possible, for one or more of the given expressions, display the given expression, a tape diagram, and a statement about percent increase or decrease next to each other.

14.3: Rewriting Expressions (15 minutes)

CCSS Standards


Addressing

Routines and Materials


Required Materials

Activity

The purpose of this activity is for students to practice rewriting expressions representing percent change so that they only use multiplication.

Launch

Allow students to work with a partner or individually.

Student Facing

  1. Write an equivalent expression using the distributive property:
    1. \(65 - 0.45 \boldcdot 65\)
    2. \(65 + 0.45 \boldcdot 65\)
    3. \(91 \boldcdot (1.2)\)
    4. \(x + 0.04x\)
  2. Evaluate by multiplying just two numbers in your calculator. Write down the expression you calculated.
    1. 130 increased by 10%
    2. 25 decreased by 30%
    3. 50% more than 38
    4. 6% less than 200
  3. Write an equivalent expression that only uses multiplication:
    1. \(p - 0.35p\)
    2. \(z - 0.85z\)
    3. \(q + 0.06q\)
    4. \(r + 0.64r\)

Student Response

For access, consult one of our IM Certified Partners.

Activity Synthesis

Either display the correct solutions or invite students to share their solutions. Here are sample questions to promote discussion:

  • “Why is it okay to rewrite an expression like \(z - 0.85z\) so that it looks like \(0.15z\)?” (Use the distributive property, or think about how an amount decreased by 85% is the same as 15% of the amount.)
  • “Have you heard some examples of percent increase or decrease used in the real world? What were they?” (Sample response: The news might talk about crime decreasing by 10% compared to last year, or home prices in an area increasing by 25%.)
  • “How is an expression representing percent increase (like \(1.05x\)) different from an expression representing percent decrease (like \(0.95x\))?” (The coefficient is greater than 1 versus less than 1. This is a result of adding or subtracting a percentage of the original amount.)