Lesson 14

Percent Increase and Decrease

  • Let’s express increasing or decreasing by a percentage using only multiplication.

14.1: Visualizing Percent Change

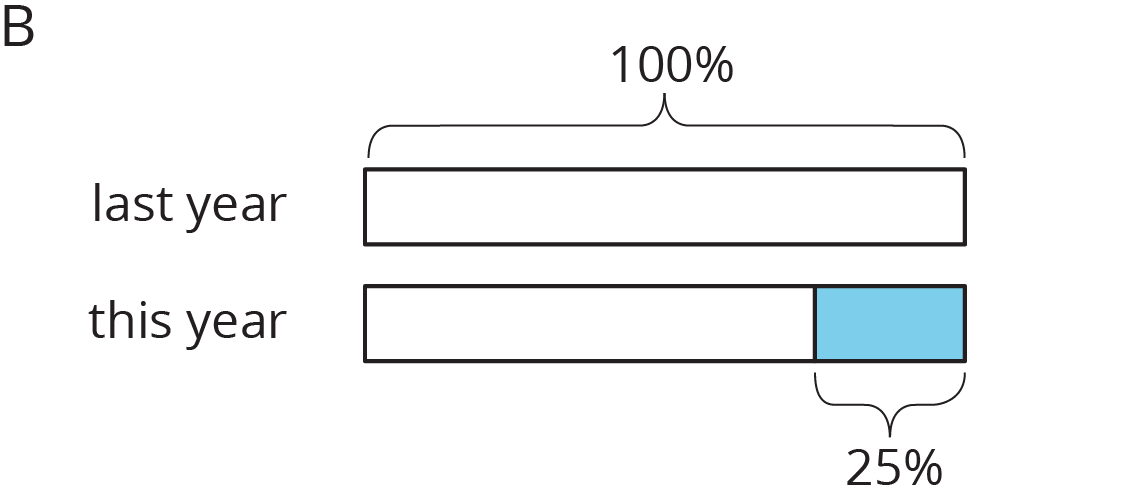
Two tape diagrams. Last year, labeled 100 percent, one long section. This year, with a smaller blue section labeled 25 percent that extends past the 100 percent tape.

Two tape diagrams. Last year, labeled 100 percent, one long section. This year, with a smaller blue section labeled 25 percent.

  1. Match each situation to a diagram. Be prepared to explain your reasoning.
    1. Compared with last year’s student population, this year’s student population increased 25%.
    2. This year’s student population is 75% of last year’s.
    3. Compared with last year, this year’s student population decreased 25%.
    4. This year’s student population is 125% of last year’s student population.
  2. Draw a diagram to represent these situations.
    1. The number of ducks living at the pond increased by 50%.
    2. The number of mosquitoes decreased by 20%.

14.2: Computing Percent Change Efficiently

An article in the paper says that the local high school’s student population will increase by 10% next year. Diego knows that this year, about 1,300 students attend the high school, and he wants to figure out next year’s population. First, he draws this diagram.

Diagram. 1300 = 100%.1300 and unknown number = 110%.
Here is his work:

  • \(1,\!300 + 0.1(1,\!300)\)
  • \(1,\!300(1 + 0.1)\)
  • \(1,\!300(1.1)\)
  • Multiplying 1,300 by 1.1, he gets 1,430.
  1. Explain each step in Diego’s method. Why does it work?
  2. Use Diego’s method to rewrite each expression so that it only uses multiplication:
    1. \(7 + 0.4 \boldcdot 7\)
    2. \(24 + 0.08 \boldcdot 24\)
    3. \(13 - 0.1 \boldcdot 13\)
    4. \(98 + 98 \boldcdot 0.02\)
  3. The first calculation gives 7 increased by 40%. What do the other calculations give, as a percent change?

14.3: Rewriting Expressions

  1. Write an equivalent expression using the distributive property:
    1. \(65 - 0.45 \boldcdot 65\)
    2. \(65 + 0.45 \boldcdot 65\)
    3. \(91 \boldcdot (1.2)\)
    4. \(x + 0.04x\)
  2. Evaluate by multiplying just two numbers in your calculator. Write down the expression you calculated.
    1. 130 increased by 10%
    2. 25 decreased by 30%
    3. 50% more than 38
    4. 6% less than 200
  3. Write an equivalent expression that only uses multiplication:
    1. \(p - 0.35p\)
    2. \(z - 0.85z\)
    3. \(q + 0.06q\)
    4. \(r + 0.64r\)

Summary