Lesson 9
Which Variable to Solve for? (Part 2)
9.1: Faces, Vertices, and Edges (5 minutes)
Warm-up
In this warm-up, students are given a simple equation in three variables and are prompted to rearrange it to pin down a particular variable. In each question, only the value of one variable is given, so students need to manipulate the equation even when some quantities are unknown. The work here prepares students to rearrange other variable equations later in the lesson.
As students work, look for those who substitute the given value before rearranging and those who first isolate the variable of interest before substituting. Invite them to share their approaches during class discussion.
Student Facing
In an earlier lesson, you saw the equation \(V + F - 2 = E\), which relates the number of vertices, faces, and edges in a Platonic solid.
-
Write an equation that makes it easier to find the number of vertices in each of the Platonic solids described:
- An octahedron (shown here), which has 8 faces.
- An icosahedron, which has 30 edges.
-
A Buckminsterfullerene (also called a “Buckyball”) is a polyhedron with 60 vertices. It is not a Platonic solid, but the numbers of faces, edges, and vertices are related the same way as those in a Platonic solid.
Write an equation that makes it easier to find the number of faces a Buckyball has if we know how many edges it has.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may be unclear what it means to write an equation that "makes it easier to find the number of vertices (or faces)." Remind them of the work in an earlier activity. In the post-parade clean-up activity, for instance, they wrote the equation \(\ell = \frac{2}{n}\) to quickly find the length of the road section each volunteer would clean up, \(\ell\), if there were \(n\) volunteers. They wrote \(n=\frac{2}{\ell}\) to quickly find the number of volunteers, \(n\), if each volunteer were to clean up \(\ell\) miles.
Activity Synthesis
Select previously identified students to share their responses and strategies. Record and display for all to see the steps they take to rearrange the equations. Emphasize how each step constitutes an acceptable move and how it keeps the equation true.
Make sure students see that we can either substitute known values into the given equation before rearranging it, or we can rearrange the equation first before substituting known values. In the examples here, it doesn't matter which way it is done. Ultimately, we were solving for \(V\) in the first question and for \(F\) in the second question.
Explain that there will be times when one strategy might be more helpful than the other, as students will see in subsequent activities.
9.2: Cargo Shipping (20 minutes)
Activity
This activity encourages students to write an equation in two variables to represent a constraint and then solve for each of the variables. One motivation for rearranging the equation is to find an expression that, when entered into a calculator or computer, can then be used to quickly find the value of one quantity given the value of the other.
As they use spreadsheet technology to create mathematical models, test them, and solve problems, students engage in aspects of mathematical modeling (MP4).
Launch
Arrange students in groups of 3–4 and instruct students to open the GeoGebra Spreadsheet available under Math Tools.
Give students a few minutes of quiet time to think about the first question and then time to discuss their responses with their group. Ask students to pause for a class discussion, and ensure everyone is using a correct equation before proceeding.
Once students have responses for the second question, invite them to share how they found the number of cars that can be shipped if the cargo already has some number of trucks. Next, ask for the expressions they wrote to find the number of cars that can fit if there are \(t\) trucks. Record the expressions for all to see.
Tell students that we can test the expressions by using a calculator or computer. Consider demonstrating how to use technology to calculate the number of cars given the number of trucks. Here is an example using the table function in Desmos: https://www.desmos.com/calculator/pbkc6levg0, and one using the slider function: https://www.desmos.com/calculator/2porjwvdm3.
For the GeoGebra Spreadsheet tool, consider using these instructions:
- In a blank spreadsheet, label the cells A1 and B1 with “trucks” and “cars.”
- In the cell A2, enter the value 480 for the number of trucks.
- In the cell B2, enter “=(21600 - 7.5*A2)/3.6” (or an equivalent expression that students wrote) and click “return.”
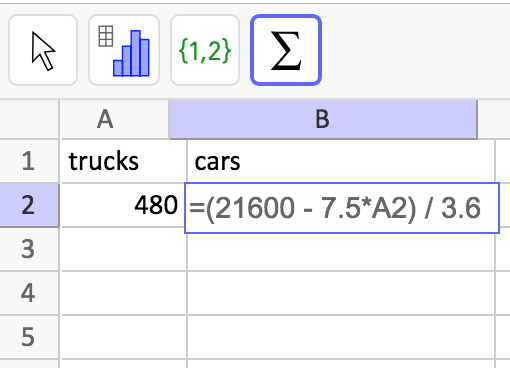
- The cell B2 should show 5,000, which is the value students should have found earlier.
- In A2, enter the other numbers of trucks students were given earlier: 1,500 and 2,736. In B2, the corresponding numbers of cars, 2,875 and 300, should appear.
Tell students that their job in the last question is to find the number of trucks when the number of cars is known. Encourage them to test their equations using technology.
Supports accessibility for: Language; Memory
Student Facing
An automobile manufacturer is preparing a shipment of cars and trucks on a cargo ship that can carry 21,600 tons.
The cars weigh 3.6 tons each and the trucks weigh 7.5 tons each.

- Write an equation that represents the weight constraint of a shipment. Let \(c\) be the number of cars and \(t\) be the number of trucks.
-
For one shipment, trucks are loaded first and cars are loaded afterwards. (Even though trucks are bulkier than cars, a shipment can consist of all trucks as long as it is within the weight limit.)
Find the number of cars that can be shipped if the cargo already has:
- 480 trucks
- 1,500 trucks
- 2,736 trucks
- \(t\) trucks
-
For a different shipment, cars are loaded first, and then trucks are loaded afterwards.
- Write an equation you could enter into a calculator or a spreadsheet tool to find the number of trucks that can be shipped if the number of cars is known.
- Use your equation and a calculator or a computer to find the number of trucks that can be shipped if the cargo already has 1,000 cars. What if the cargo already has 4,250 cars?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 3–4 and provide access to devices with spreadsheet or graphing technology.
Give students a few minutes of quiet time to think about the first question and then time to discuss their responses with their group. Ask students to pause for a class discussion, and ensure everyone is using a correct equation before proceeding.
Once students have responses for the second question, invite them to share how they found the number of cars that can be shipped if the cargo already has some number of trucks. Next, ask for the expressions they wrote to find the number of cars that can fit if there are \(t\) trucks. Record the expressions for all to see.
Tell students that we can test the expressions by using a calculator or computer. Consider demonstrating how to use technology to calculate the number of cars given the number of trucks. For examples using a table, sliders, and a spreadsheet, see the digital version of this activity. You may need to prepare alternate instructions if using different technology in the classroom.
Tell students that their job in the last question is to find the number of trucks when the number of cars is known. Encourage them to test their equations using available technology.
Supports accessibility for: Language; Memory
Student Facing
An automobile manufacturer is preparing a shipment of cars and trucks on a cargo ship that can carry 21,600 tons.
The cars weigh 3.6 tons each and the trucks weigh 7.5 tons each.

- Write an equation that represents the weight constraint of a shipment. Let \(c\) be the number of cars and \(t\) be the number of trucks.
-
For one shipment, trucks are loaded first and cars are loaded afterwards. (Even though trucks are bulkier than cars, a shipment can consist of all trucks as long as it is within the weight limit.)
Find the number of cars that can be shipped if the cargo already has:
- 480 trucks
- 1,500 trucks
- 2,736 trucks
- \(t\) trucks
-
For a different shipment, cars are loaded first, and then trucks are loaded afterwards.
- Write an equation you could enter into a calculator or a spreadsheet tool to find the number of trucks that can be shipped if the number of cars is known.
- Use your equation and a calculator or a computer to find the number of trucks that can be shipped if the cargo already has 1,000 cars. What if the cargo already has 4,250 cars?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
For yet another shipment, the manufacturer is also shipping motorcycles, which weigh 0.3 ton each.
- Write an equation that you could enter into a calculator or a spreadsheet tool to find the number of motorcycles that can be shipped, \(m\), if the number of cars and trucks are known.
- Use your equation to find the number of motorcycles that can be shipped if the cargo already contains 1,200 trucks and 3,000 cars.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
When finding the number of cars, \(c\), given \(t\) trucks, students may have arrived at the expression \(\dfrac {21,600 - 7.5t}{3.6}\) by generalizing the calculation they performed when the number of trucks was a numerical value. Likewise, in the last question they may have arrived at \(t = \dfrac{21,600 - 3.6c}{7.5}\) by using some numerical values for \(c\) and generalizing the process.
While this strategy is expected and perfectly reasonable, make sure students also see that we can arrive at the same expression for \(c\) and for \(t\) by rearranging the equation \(3.6c + 7.5t = 21,\!600\).
Highlight that we can solve for \(c\) when we know the number of trucks and want to compute the number of cars, and solve for \(t\) when we know the number of cars and want to find the number of trucks.
\(\begin {align} 3.6c + 7.5t &= 21,\!600\\ 3.6c &= 21,\!600 - 7.5t\\ c&=\dfrac {21,\!600 - 7.5t}{3.6} \end{align}\)
\(\begin {align} 3.6c + 7.5t &= 21,\!600\\ 7.5t &= 21,\!600 - 3.6c\\ t &=\dfrac {21,\!600 - 3.6c}{7.5} \end{align}\)
9.3: Streets and Staffing (10 minutes)
Activity
This activity gives students another opportunity to write and rearrange equations in two variables and to do so in context.
Unlike in previous activities, students no longer start by computing one quantity given numerical values of the other quantity and then generalizing the process. Instead, they are prompted to write one equation, solve for each variable, and interpret the solution. Students also articulate why one model might be more helpful than the other under a certain circumstance. Along the way, students reason quantitatively and abstractly (MP2) and engage in aspects of modeling (MP4).
Making spreadsheet technology available gives students an opportunity to choose appropriate tools strategically (MP5).
Launch
Familiarize students with the idea of organizational budgets, if needed. Explain that every governmental agency has a budget (not unlike a budget for a pizza party) and needs to decide how to allocate a limited amount of funds. Ask students to think of examples of expenses that a city's Department of Streets might have (road repairs, new street construction, additional workers, new equipment, and so on). Given a set budget, spending more on one thing means having less to spend on something else, so the agency would need to weigh their options and prioritize their needs.
Design Principle(s): Support sense-making
Supports accessibility for: Language; Conceptual processing
Student Facing
The Department of Streets of a city has a budget of \$1,962,800 for resurfacing roads and hiring additional workers this year.
The cost of resurfacing a mile of 2-lane road is estimated at \$84,000. The average starting salary of a worker in the department is \$36,000 a year.

- Write an equation that represents the relationship between the miles of 2-lane roads the department could resurface, \(m\), and the number of new workers it could hire, \(p\), if it spends the entire budget.
- Take the equation you wrote in the first question and:
- Solve for \(p\). Explain what the solution represents in this situation.
- Solve for \(m\). Explain what the solution represents in this situation.
- The city is planning to hire 6 new workers and to use its entire budget.
- Which equation should be used to find out how many miles of 2-lane roads it could resurface? Explain your reasoning.
- Find the number of miles of 2-lane roads the city could resurface if it hires 6 new workers.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may have trouble sorting out the given information because of unfamiliarity with the context or with certain terms. Ask them to explain the setup of the problem as best they understand it, and then point out any information that might be missing.
Activity Synthesis
Verify that the equations students wrote correctly isolate each variable. If students wrote expressions in different forms for a variable (for instance, \(\dfrac {4,\!907 - 210m}{90}\) and \(\dfrac {1,\!962,\!800 -84,\!000m}{36,\!000}\) for \(p\)), discuss how the expressions are equivalent.
If time permits, consider asking students to use their equations to answer these questions:
- "How many people could be hired if the department is resurfacing 16 miles of roads?" (17 people) "3 miles?" (47 people)
- "How many miles of roads could be resurfaced if the department is hiring 2 new workers?" (22.5 miles) "If no new workers are hired?" (About 23.37 miles)
Make sure students understand that solving for \(p\) makes it possible to quickly find the number of people that the department could hire given some miles of road to be resurfaced (and while sticking to the budget). Similarly, solving for \(m\) makes it possible to quickly find the miles that could be resurfaced given any number of new hires.
Lesson Synthesis
Lesson Synthesis
Decribe and display the following situation to students.
Suppose you are organizing a party and have a budget of \(b\) dollars for the appetizers. You plan to order \(v\) vegetarian spring rolls at \$0.75 each and \(s\) shrimp rolls at \$0.95 each. The equation \(0.75v + 0.95s = b\) represents this constraint.
Ask one half of the class to solve for \(v\) and the other half to solve for \(s\).
Then, ask students: "When might it be most handy to use each of these equations in your party planning?"
- \(0.75v + 0.95s = b\) (When we want to find out how much different combinations or rolls would cost.)
- \(v = \dfrac {b - 0.95s}{0.75}\) (When we know the budget and want to find out how many vegetarian rolls we could get if we order different numbers of shrimp rolls.)
- \(s = \dfrac {b - 0.75v}{0.95}\) (When we know the budget and want to find out how many shrimp rolls we could get if we order different numbers of vegetarian rolls.)
9.4: Cool-down - Carnival Tickets (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Solving for a variable is an efficient way to find out the values that meet the constraints in a situation. Here is an example.
An elevator has a capacity of 3,000 pounds and is being loaded with boxes of two sizes—small and large. A small box weighs 60 pounds and a large box weighs 150 pounds.
Let \(x\) be the number of small boxes and \(y\) the number of large boxes. To represent the combination of small and large boxes that fill the elevator to capacity, we can write:
\(60x + 150y = 3,\!000\)
If there are 10 large boxes already, how many small boxes can we load onto the elevator so that it fills it to capacity? What if there are 16 large boxes?
In each case, we can substitute 10 or 16 for \(y\) and perform acceptable moves to solve the equation. Or, we can first solve for \(x\):
\(\begin {align} 60x + 150y &= 3,\!000 &\quad &\text{original equation}\\ 60x &=3,\!000 - 150y &\quad &\text{subtract }150y \text{ from each side}\\ x &=\dfrac {3,000-150y}{60} &\quad &\text{divide each side by 60} \end{align}\)
This equation allows us to easily find the number of small boxes that can be loaded, \(x\), by substituting any number of large boxes for \(y\).
Now suppose we first load the elevator with small boxes, say, 30 or 42, and want to know how many large boxes can be added for the elevator to reach its capacity.
We can substitute 30 or 42 for \(x\) in the original equation and solve it. Or, we can first solve for \(y\):
\(\begin {align} 60x + 150y &= 3,\!000 &\quad &\text{original equation}\\ 150y &=3,\!000 - 60x &\quad &\text{subtract }60x \text{ from each side}\\ y&=\dfrac {3,000-60x}{150} &\quad &\text{divide each side by 150} \end{align}\)
Now, for any value of \(x\), we can quickly find \(y\) by evaluating the expression on the right side of the equal sign.
Solving for a variable—before substituting any known values—can make it easier to test different values of one variable and see how they affect the other variable. It can save us the trouble of doing the same calculation over and over.
