Lesson 9
Using Trigonometric Ratios to Find Angles
- Let’s work backwards to find angles in right triangles.
Problem 1
Technology required. Ramps in a parking garage need to be both steep and safe. The maximum safe incline for a ramp is 8.5 degrees. Is this ramp safe? If not, provide dimensions that would make the ramp safe.
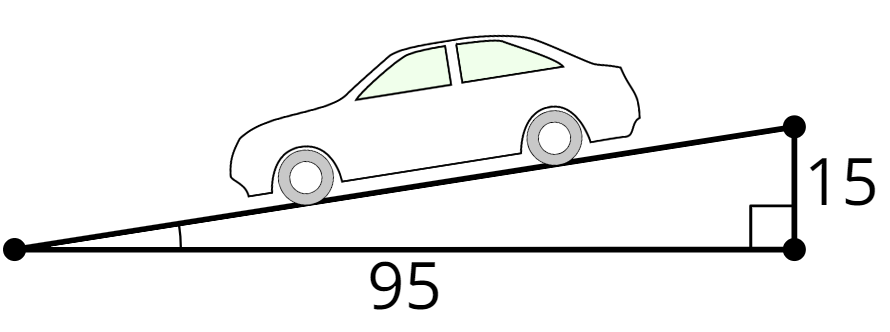
Problem 2
Technology required. \(ABCD\) is a rectangle. Find the length of \(AC\) and the measures of \(\alpha\) and \(\theta\).

Problem 3
Technology required. Find the missing measurements.

Problem 4
Select all the true equations:

\(\sin(27) =\frac{x}{15}\)
\(\cos(63) =\frac{y}{15}\)
\(\tan(27) = \frac{y}{x}\)
\(\sin(63) = \frac{x}{15}\)
\(\tan(63) = \frac{y}{x}\)
Problem 5
What value of \(\theta\) makes this equation true? \(\sin(30)=\cos(\theta)\)
-30
30
60
180
Problem 6
A rope with a length of 3.5 meters is tied from a stake in the ground to the top of a tent. It forms a 17 degree angle with the ground. How tall is the tent?
\(3.5 \tan(17)\)
\(3.5 \cos(17)\)
\(3.5 \sin(17)\)
\(\frac{\sin(17)}{3.5}\)
Problem 7
Technology required. What is the value of \(x\)?

Problem 8
Find the missing side in each triangle using any method. Check your answers using a different method.

Problem 9
The triangles are congruent. Write a sequence of rigid motions that takes triangle \(XYZ\) onto triangle \(BCA\).
