Lesson 7

Applying Ratios in Right Triangles

  • Let’s solve problems by using right triangles and trigonometry.

7.1: Tilted Triangle

Calculate the lengths of sides \(AC\) and \(BC\).

Right triangle A B C. A B is 6 units, angle A C B is 90 degrees, angle A B C is 20 degrees.

7.2: Info Gap: Trigonometry

Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.

If your teacher gives you the data card:

  1. Silently read the information on your card.
  2. Ask your partner, “What specific information do you need?” and wait for your partner to ask for information. Only give information that is on your card. (Do not figure out anything for your partner!)
  3. Before telling your partner the information, ask “Why do you need to know (that piece of information)?”
  4. Read the problem card, and solve the problem independently.
  5. Share the data card, and discuss your reasoning.

If your teacher gives you the problem card:

  1. Silently read your card and think about what information you need to answer the question.
  2. Ask your partner for the specific information that you need.
  3. Explain to your partner how you are using the information to solve the problem.
  4. When you have enough information, share the problem card with your partner, and solve the problem independently.
  5. Read the data card, and discuss your reasoning.

Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.

7.3: Tallest Tower

  1. The tallest building in the world is the Burj Khalifa in Dubai (as of April 2019).

    If you’re standing on the bridge 250 meters from the bottom of the building, you have to look up at a 73 degree angle to see the top. How tall is the building? Explain or show your reasoning.

    Picture of Burj Khalifa with right triangle A B C drawn on top. Right angle C B A. Height of building, A B. Bottom leg B C labeled 250. Angle B C A labeled 73 degrees.

  2. The tallest masonry building in the world is City Hall in Philadelphia (as of April 2019). If you’re standing on the street 1,300 feet from the bottom of the building, you have to look up at a 23 degree angle to see the top. How tall is the building? Explain or show your reasoning.



You’re sitting on a ledge 300 feet from a building. You have to look up 60 degrees to see the top of the building and down 15 degrees to see the bottom of the building. How tall is the building?

Summary

Using trigonometry and properties of right triangles, we can calculate and estimate measures in different right triangles. We can use these skills to estimate unknown heights of objects that are too tall to measure directly. For example, we can't reach the top of this tree with a measuring tape.

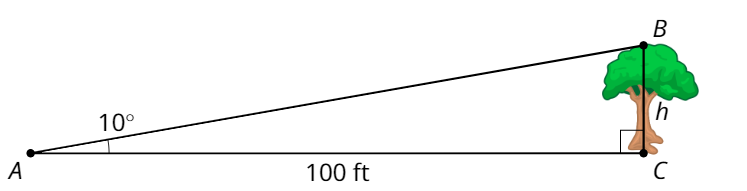
Triangle A B C where B C is the height of a tree. Angle A is 10 degrees, angle C is a right angle, and segment A C is 100 feet.

To calculate the height of the tree, we could stand where the angle between the top and bottom of the tree is 10 degrees. Since we know the distance to the tree (the adjacent leg) and would like to know the height (the opposite leg), we need to use tangent. So \(\tan(10)=\frac{h}{100}\). In the calculator we can look up that \(\tan(10)\) is 0.176. Then we can calculate that \(h\) is about 17.6. That means the tree is 17.6 feet tall.

Glossary Entries

  • cosine

    The cosine of an acute angle in a right triangle is the ratio (quotient) of the length of the adjacent leg to the length of the hypotenuse. In the diagram, \(\cos(x)=\frac{b}{c}\).

  • sine

    The sine of an acute angle in a right triangle is the ratio (quotient) of the length of the opposite leg to the length of the hypotenuse. In the diagram, \(\sin(x) = \frac{a}{c}.\)

  • tangent

    The tangent of an acute angle in a right triangle is the ratio (quotient) of the length of the opposite leg to the length of the adjacent leg. In the diagram, \(\tan(x) = \frac{a}{b}.\)

  • trigonometric ratio

    Sine, cosine, and tangent are called trigonometric ratios.