Lesson 5
Working with Ratios in Right Triangles
- Let’s solve problems about right triangles.
Problem 1
A triangle has sides with lengths 8, 15, and 17.
- Verify this is a Pythagorean triple.
- Approximate the acute angles in this triangle.
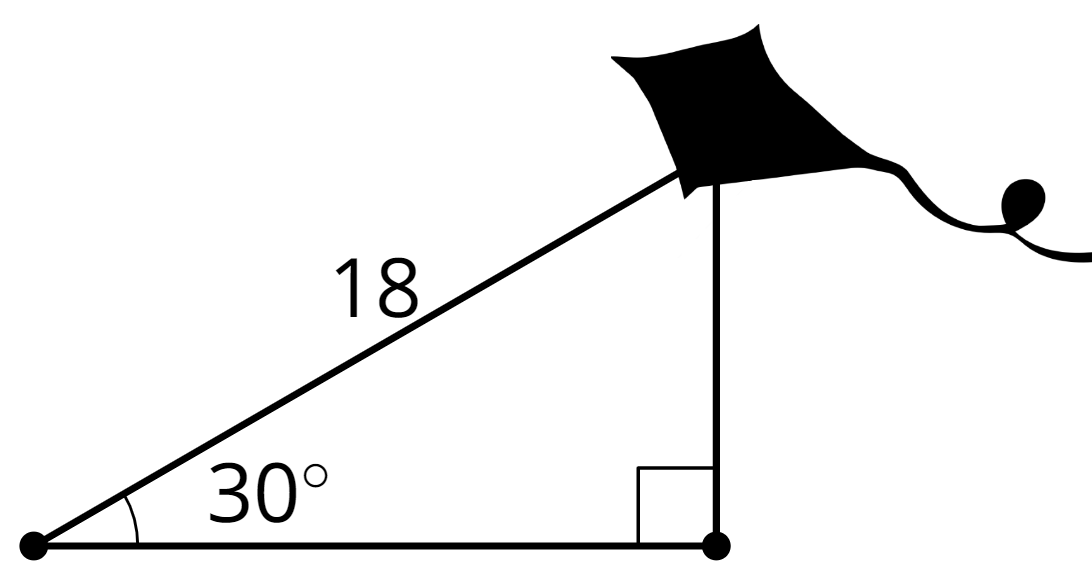
Problem 2
Kiran is flying a kite. He gets tired, so he stakes the kite into the ground. The kite is on a string that is 18 feet long and makes a 30 degree angle with the ground. How high is the kite?
Problem 3
Triangle \(ABC\) has a right angle at \(C\). Select all measurements which would mean it has a hypotenuse with a length of 10 units.

Angle \(A\) is 20 degrees, \(BC\) is 2 units
\(AC\) is 7 units, \(BC\) is 3 units
Angle \(B\) is 50 degrees, \(BC\) is 4 units
Angle \(A\) is 30 degrees, \(BC\) is 5 units
\(AC\) is 8 units, \(BC\) is 6 units
Problem 4
What is a reasonable approximation for angle \(B\) if the ratio of the adjacent leg divided by the hypotenuse is 0.45?
27 degrees
30 degrees
60 degrees
63 degrees
Problem 5
Estimate the values to complete the table.

| angle | adjacent leg \(\div\) hypotenuse | opposite leg \(\div\) hypotenuse | opposite leg \(\div\) adjacent leg |
|---|---|---|---|
| \(A\) | 0.31 | 0.95 | 3.1 |
| \(C\) |
Problem 6
What is the length of side \(AB\)?

Problem 7
What is the length of the square’s side?

3 units
\(\frac{6}{\sqrt2}\) units
\(6 \sqrt2\) units
12 units
Problem 8
Find the lengths of segments \(AD\) and \(BD\). Then check your answers using a different method.
