Lesson 18
Using Functions to Model Battery Power
- Let’s use functions to model data and make predictions.
18.1: Devices
Think about an electronic device with a battery that you have to charge on a regular basis.
- What device is it?
- When you are using the device, about how long does it take the battery to go from 100% charged until the time you plug it in again to recharge?
- About how long does it take to charge to 100% starting from 0% or nearly 0%?
-
Suppose you plugged in your device when the battery was 50% charged.
How long do you think it would take to recharge the device to 100% compared to the time it would take if the device was at 0%? Would it be exactly half the time, more than half the time, or less than half the time it would take if starting from 0%?
18.2: Charging a Phone
A cell phone is plugged in to be charged. The table shows the percent of battery power at some times after it was plugged in.
| time | percent charged |
|---|---|
| 11:00 a.m. | 6% |
| 11:10 a.m. | 15% |
| 11:30 a.m. | 35% |
| 11:40 a.m. | 43% |
At what time will the battery be 100% charged? Use the data to find out and explain or show your reasoning.
18.3: How Long Will It Last?
-
The image shows the battery usage of a cell phone 9 hours since it was fully charged.
It also shows a prediction that the battery would last 8 more hours.
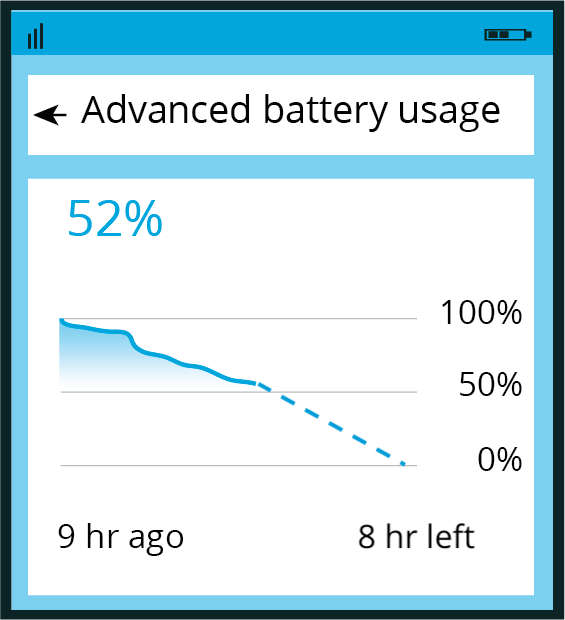
-
Write an equation for a model that fits the data in the image and gives the percent of battery power, \(p\), as a function of time since the phone was fully charged, \(t\). Show your reasoning.
If you get stuck, consider creating a table of values or a scatter plot of the data.
- Based on your function, what percentage of power would the battery have 4 hours after this image was taken? What about 5 hours after the image was taken? Show your reasoning.
-
- Here are two more images showing the battery usage at two later times, before the battery was charged again.
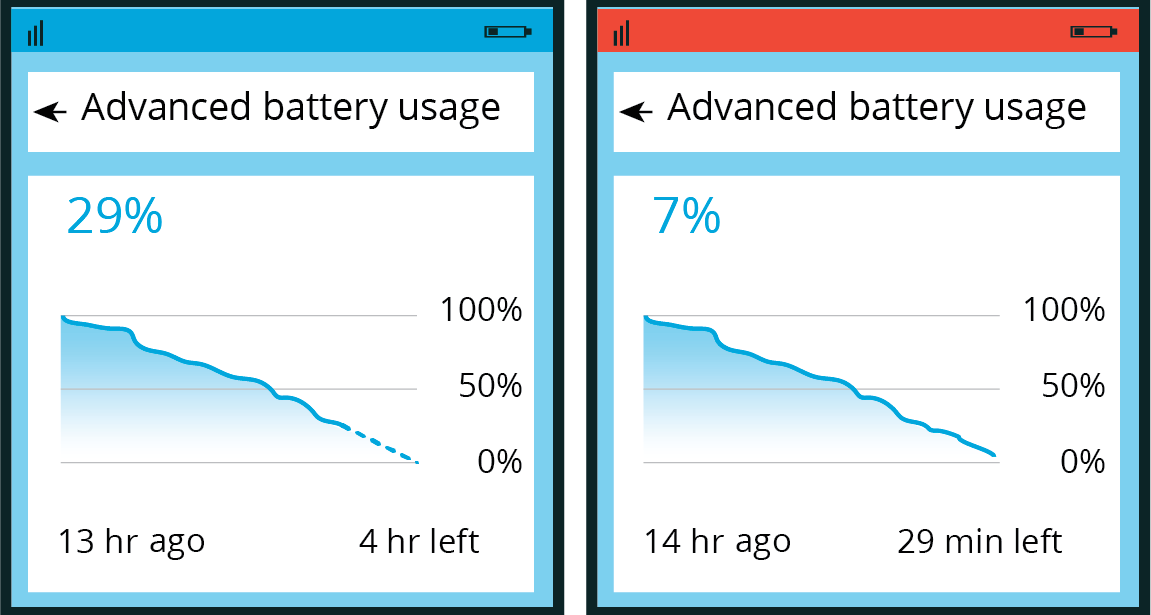
- How well did the function you wrote predict the battery power 4 and 5 hours since the first image was taken (that is, 13 and 14 hours after the battery was fully charged)? Explain or show your reasoning.
- What do you notice from the images about the change in the prediction between \(t=13\) and \(t=14\)?
- Write a new equation for a function that would better fit the data shown in the last image.
Would a piecewise function be a better model for capturing the data shown in all three images? If so, what might the rules of that function be?