Lesson 1
Describing and Graphing Situations
- Let’s look at some fun functions around us and try to describe them!
1.1: Bagel Shop


A customer at a bagel shop is buying 13 bagels. The shopkeeper says, “That would be $16.25.”
Jada, Priya, and Han, who are in the shop, all think it is a mistake.
- Jada says to her friends, “Shouldn’t the total be \$13.25?”
- Priya says, “I think it should be \$13.00.”
- Han says, “No, I think it should be \$11.25.”
Explain how the shopkeeper, Jada, Priya, and Han could all be right.
Your teacher will give you instructions for completing the table.
| number of bagels |
|
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 |
1.2: Be Right Back!
Three days in a row, a dog owner tied his dog’s 5-foot-long leash to a post outside a store while he ran into the store to get a drink. Each time, the owner returned within minutes.
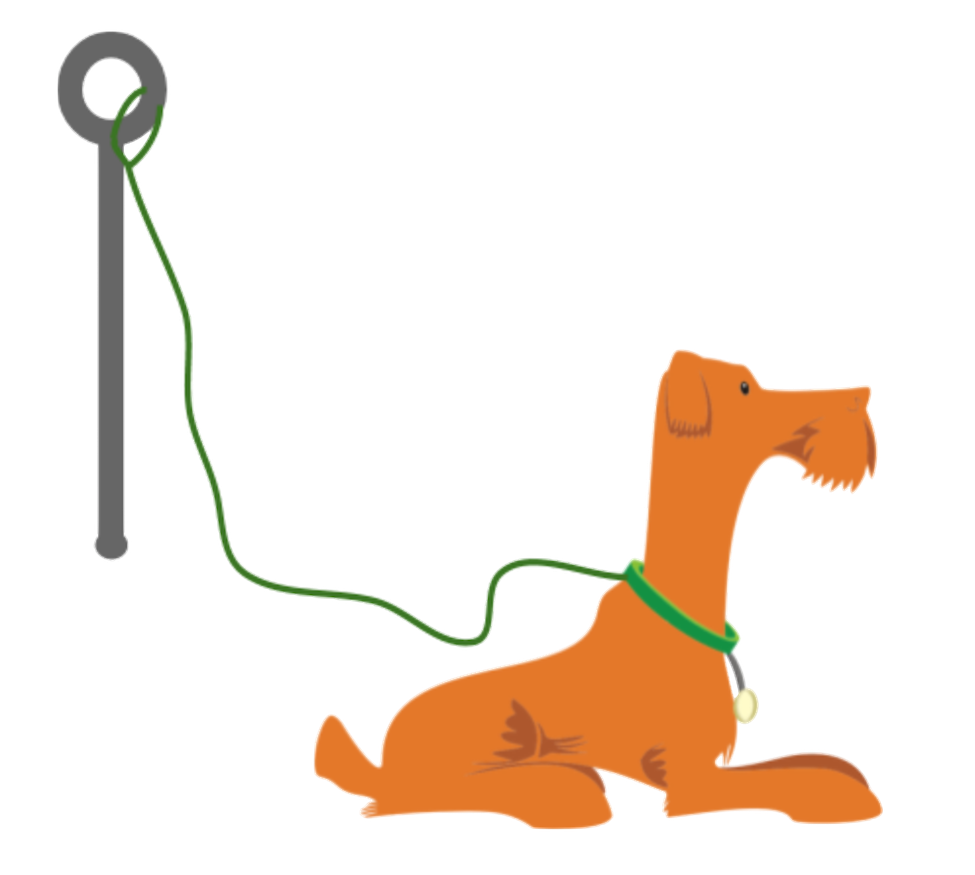
The dog’s movement each day is described here.
- Day 1: The dog walked around the entire time while waiting for its owner.
- Day 2: The dog walked around for the first minute, and then laid down until its owner returned.
- Day 3: The dog tried to follow its owner into the store but was stopped by the leash. Then, it started walking around the post in one direction. It kept walking until its leash was completely wound up around the post. The dog stayed there until its owner returned.
- Each day, the dog was 1.5 feet away from the post when the owner left.
- Each day, 60 seconds after the owner left, the dog was 4 feet from the post.
Your teacher will assign one of the days for you to analyze.
Sketch a graph that could represent the dog’s distance from the post, in feet, as a function of time, in seconds, since the owner left.
Day \(\underline{\hspace{0.5in}}\)

From the graph, is it possible to tell how many times the dog changed directions while walking around? Explain your reasoning.
1.3: Talk about a Function
Here are two pairs of quantities from a situation you’ve seen in this lesson. Each pair has a relationship that can be defined as a function.
- time, in seconds, since the dog owner left and the total number of times the dog has barked
- time, in seconds, since the owner left and the total distance, in feet, that the dog has walked while waiting
Choose one pair of quantities and express their relationship as a function.
- In that function, which variable is independent? Which one is dependent?
- Write a sentence of the form “\(\underline{\hspace{0.5in}}\) is a function of \(\underline{\hspace{0.5in}}\).”
-
Sketch a possible graph of the relationship on the coordinate plane. Be sure to label and indicate a scale on each axis, and be prepared to explain your reasoning.
Summary
A relationship between two quantities is a function if there is exactly one output for each input. We call the input the independent variable and the output the dependent variable.
Let’s look at the relationship between the amount of time since a plane takes off, in seconds, and the plane’s height above the ground, in feet.
-
These two quantities form a function if time is the independent variable (the input) and height is the dependent variable (the output). This is because at any amount of time since takeoff, the plane could only be at one height above the ground.
For example, 50 seconds after takeoff, the plane might have a height of 180 feet. At that moment, it cannot be simultaneously 180 feet and 95 feet above the ground.
For any input, there is only one possible output, so the height of the plane is a function of the time since takeoff.
-
The two quantities do not form a function, however, if we consider height as the input and time as the output. This is because the plane can be at the same height for multiple lengths of times since takeoff.
For instance, when the plane is 1,500 feet above ground, it is possible that 300 seconds have passed. It is also possible that 425 seconds, 275 seconds, or some other amounts of time have passed.
For any input, there are multiple possible outputs, so the time since takeoff is not a function of the height of the plane.
Functions can be represented in many ways—with a verbal description, a table of values, a graph, an expression or an equation, or a set of ordered pairs.
When a function is represented with a graph, each point on the graph is a specific pair of input and output.
Here is a graph that shows the height of a plane as a function of time since takeoff.

The point \((125, 400)\) tells us that 125 seconds after takeoff, the height of the plane is 400 feet.
Glossary Entries
- dependent variable
A variable representing the output of a function.
The equation \(y = 6-x\) defines \(y\) as a function of \(x\). The variable \(x\) is the independent variable, because you can choose any value for it. The variable \(y\) is called the dependent variable, because it depends on \(x\). Once you have chosen a value for \(x\), the value of \(y\) is determined.
- function
A function takes inputs from one set and assigns them to outputs from another set, assigning exactly one output to each input.
- independent variable
A variable representing the input of a function.
The equation \(y = 6-x\) defines \(y\) as a function of \(x\). The variable \(x\) is the independent variable, because you can choose any value for it. The variable \(y\) is called the dependent variable, because it depends on \(x\). Once you have chosen a value for \(x\), the value of \(y\) is determined.
