Lesson 11
Different Partial Quotients
Warm-up: Notice and Wonder: Ways to Record (10 minutes)
Narrative
Launch
- Groups of 2
- Display the image.
- “What do you notice? What do you wonder?”
- 1 minute: quiet think time
Activity
- “Discuss your thinking with your partner.”
- 1 minute: partner discussion
- Share and record responses.
Student Facing
What do you notice? What do you wonder?
Clare’s strategy:
Jada’s strategy:
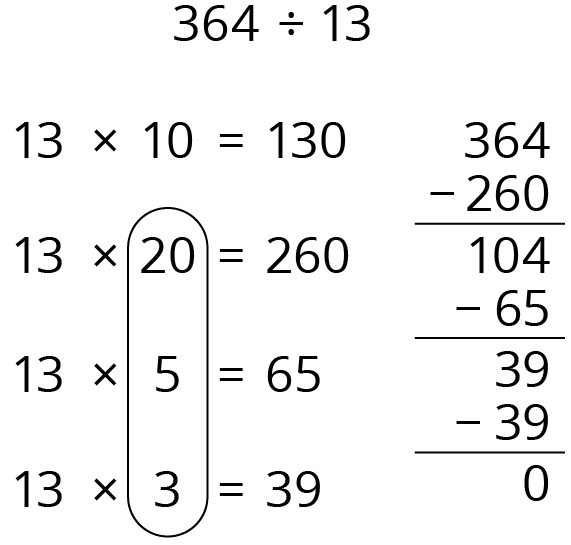
\(\begin{align} 130\div 13&= 10\\ 130\div 13 &= 10\\ 65 \div 13 &= \phantom{0} 5\\ 39\div 13 &= \phantom{0} 3\\ \overline {\hspace{5mm}364 \div 13} &\overline{\hspace{1mm}= 28 \phantom{000}}\end{align}\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “How are these strategies the same and different as the way you found quotients in the previous lesson?” (They use multiplication and division. They break the problem into smaller parts with numbers that are easier to calculate.)
- “Multiplication can help us think about partial quotients.”
Activity 1: Division Expressions (20 minutes)
Narrative
The purpose of this activity is to see that some equivalent ways of rewriting a division expression are more helpful than others for finding its value. In particular expressions whose value can be calculated mentally are most helpful. This supports students when they choose their own ways of breaking up the dividend when they use an algorithm that uses partial products in future lessons.
When they identify expressions to find the value of a quotient, students notice that dividends that are readily identifiable as multiples of 14 are most useful for finding the value of the quotient (MP7).
This activity uses MLR2 Collect and Display. Advances: Conversing, Reading, Writing.
Supports accessibility for: Organization, Conceptual Processing, Language
Required Materials
Materials to Copy
- Partial Quotient Expressions
Required Preparation
- Create a set of cards from the blackline master for each group of 2.
Launch
- Groups of 2
- Display cards for the activity.
- “What do you notice? What do you wonder?” (They all have a 14 in them. Some of the expressions are repeated. All of them show a number being divided by 14. A lot of the expressions show multiples of 10. A lot of the expressions show multiples of 14. I wonder what we are going to do with these expressions. I wonder why they all divide a number by 14?)
- “You are going to choose expressions that represent a sum that is equal to \(308 \div 14\).”
- “Keep each set of expressions that you choose.”
Activity
- 3–5 minutes: partner work time
- As students play the game, circulate, listen for, and collect the language students use to explain how they know the cards they chose represent a sum that is equal to \(308 \div 14\). Listen for: add, plus, divide, dividend, quotient, equals, “the same as”, and groups of.
- Record students’ words and phrases on a visual display and update it throughout the lesson.
- “Choose one set of expressions and use it to find the value of \(308 \div 14\).”
- 3–5 minutes: independent work time
- Monitor for students who use these different combinations to find the value of \(308 \div 14\):
- \(280 \div 14\), \(28 \div 14\)
- \(140 \div 14\), \(140 \div 14\), \(28 \div 14\)
Student Facing
Take turns:
- Choose a set of expressions that, when added together, is equal to \(308 \div 14\). Not all expressions will be used.
-
Explain to your partner how you know that your cards represent a sum that is equal to \(308 \div 14\).
(Pause for teacher directions.)
- Choose one of the sets of expressions whose sum is equal to \(308 \div 14\) and use it to find the value of \(308 \div 14\).
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students do not recognize which expressions created by the cards would be helpful to find the value of the quotient \(308 \div 14\), ask, “Which of these expressions have a value that is a whole number? How could you use the expression to find the value of \(308 \div 14\)?”
Activity Synthesis
- Refer to the visual display of the words students used during the activity.
- “These are the words you used to explain how you knew the cards you chose represent a sum that is equal to \(308 \div 14\).”
- “Are there any other words or phrases that are important to include on our display?”
- As students share responses, update the display, by adding (or replacing) language, diagrams, or annotations.
- Remind students to borrow language from the display as needed.
- Display:
\(308 \div 14\) - Ask previously selected students to share.
- “Why did you choose that set of expressions to find the value of \(308 \div 14\)?” (I could find the values of the expressions mentally.)
- Display:
\(280 \div 14\) - “Why is \(280 \div 14\) a helpful expression to start with?” (\(280 \div 14\) is a helpful expression to start with because \(20 \times 14 = 280\) and 280 is close to 308.)
- “How do we know that \(28 \div 14\) is the expression that matches \(280 \div 14\)?” (\(280 + 28 = 308\))
Activity 2: Choose Your Own Partial Quotients (15 minutes)
Narrative
Launch
- Groups of 2
- “For these problems, choose one of the division expressions to use to begin finding the quotient. Then use the expressions you chose to find the value of each quotient."
Activity
- 6-8 minutes: independent work time
- 2-3 minutes: partner discussion
- Monitor for students who
- use different expressions for \(992\div31\).
- wrote about changing their mind in the last question.
Student Facing
For each expression, choose one of the partial quotients and, beginning with that expression, find the value of the quotient.
-
\(360\div15\)
- \(150\div15\)
- \(300\div15\)
- \(60\div15\)
-
\(945\div45\)
- \(45\div45\)
- \(450\div45\)
- \(900\div45\)
-
\(992\div31\)
- \(62\div31\)
- \(341\div31\)
- \(310\div31\)
- How did you decide which partial quotient to use to begin finding the quotient? Did you change your mind with any of the problems?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Invite selected students to share their reasoning for \(992\div31\) and explain why they started with their expression.
- Invite students to share how they changed their mind about which expressions to use during the activity.
Lesson Synthesis
Lesson Synthesis
“Today we thought strategically about which partial quotients are most helpful for finding the value of a division expression.”
Display the last problem from the second activity: \(945\div 45\).
“Diego said, ‘In order to solve division problems, you can use all the operations.’ What does Diego mean? When did we use addition, subtraction, and multiplication to divide?” (We can multiply in order to find how many 45s are in 945. After we find those multiples, we can add them up to get 945. We can also use division. I know that \(90 \div 45 = 2\) and \(900 \div 45 = 20\) so I can subtract 900 from 945 and that leaves just 1 more 45.)
Cool-down: Find the Value (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.