Lesson 9
You Ate the Whole Thing
Warm-up: Number Talk: What's the Sum? (10 minutes)
Narrative
Launch
- Display one expression.
- “Give me a signal when you have an answer and can explain how you got it.”
- 1 minute: quiet think time
Activity
- Record answers and strategies.
- Keep expressions and work displayed.
- Repeat with each expression.
Student Facing
Find the value of each expression mentally.
- \(20 + 10 + 10 + 5\)
- \(30 + 25\)
- \(35 + 15\)
- \(15 + 25 + 15\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “What patterns did you notice working with these numbers?”
- “How could the second problem help you think about the last one?” (I know that \(15 + 15 = 30\), so it was the same problem.)
Activity 1: Pizza to Share (15 minutes)
Narrative
The purpose of this activity is for students to learn that when you partition a shape into 2, 3, or 4 equal pieces, the whole shape can be named as 2 halves, 3 thirds, 4 fourths respectively. This activity uses the context of pizza to intentionally elicit “whole” from students to describe the situation. They will continue to deepen their understanding of a whole as a mathematical term during their study of fractions in grade 3. Students observe regularity in repeated reasoning (MP8) when they see that however many equal pieces the whole pizza is cut into, that number of pieces makes the whole.
Students begin the activity by looking at the problem displayed, rather than in their books. At the end of the launch, students open their books and work on the problem.
This activity uses MLR5 Co-craft Questions. Advances: writing, reading, representing.
Launch
- Groups of 2
MLR5 Co-Craft Questions
- Display only the problem stem and image for Clare’s pizza, without revealing the questions.
- “Clare’s friends were going to share a pizza. The image shows how they cut the pizza.”
- “Write a list of mathematical questions that could be asked about this situation.” (How many friends does she have? How much pizza can each friend get? Can they slice the pizza a different way? What would be a fair way to share the pizza with her friends?)
- 2 minutes: independent work time
- 2–3 minutes: partner discussion
- Invite several students to share one question with the class. Record responses.
- “What do these questions have in common? How are they different?”
- Reveal the additional context and questions for Clare’s pizza (students open books), and invite additional connections.
- “Why do you believe her friends are upset?” (The pizza is cut into thirds, so 3 slices would be the whole pizza. 3 thirds is the same as the whole thing.)
Activity
- “Now you and your partner will discuss what happened in each problem when students share a pizza.”
- 10 minutes: partner work time
Student Facing
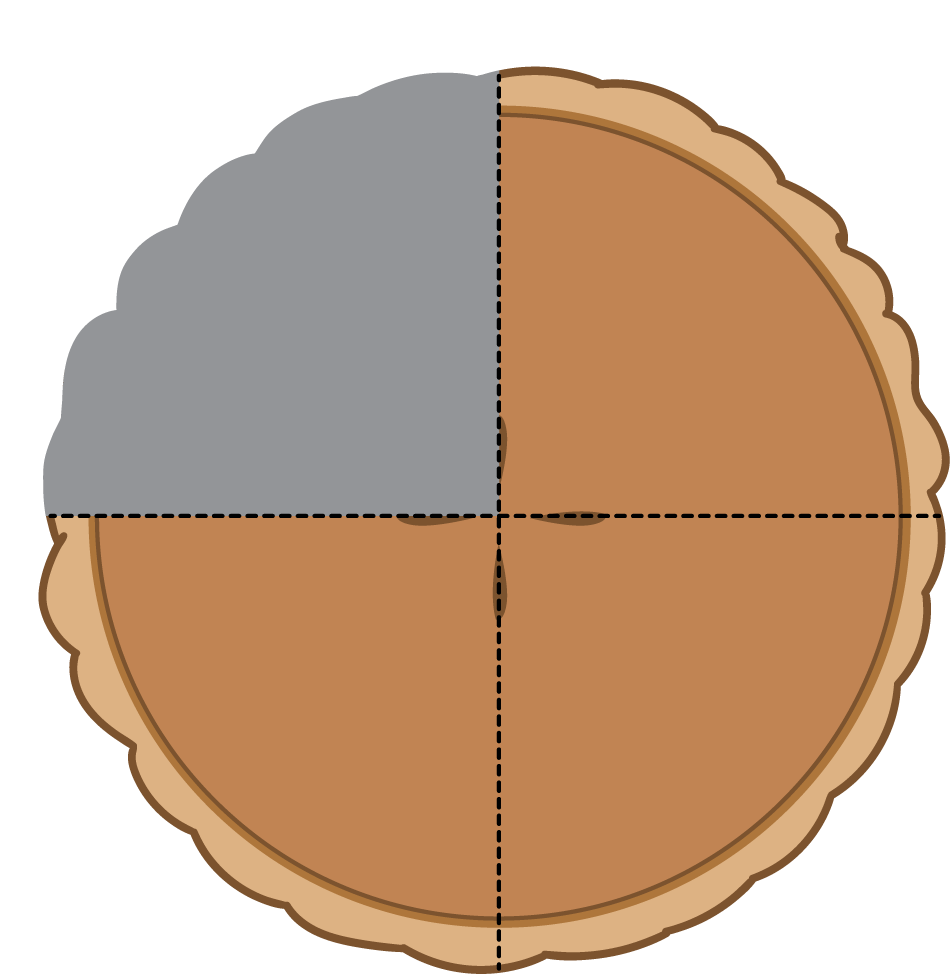
Clare’s friends were going to share a pizza. The image shows how they cut the pizza.
-
Clare ate 3 slices and her friends got upset with her.
- Why are her friends upset?
- How many thirds did Clare eat?
- How much of the pizza was left?
-
Pizza Parts

Group
Priya
Han
Diego
- Priya will eat ________________________ of the pizza.
- Together they will eat ________________________ of the pizza.
-
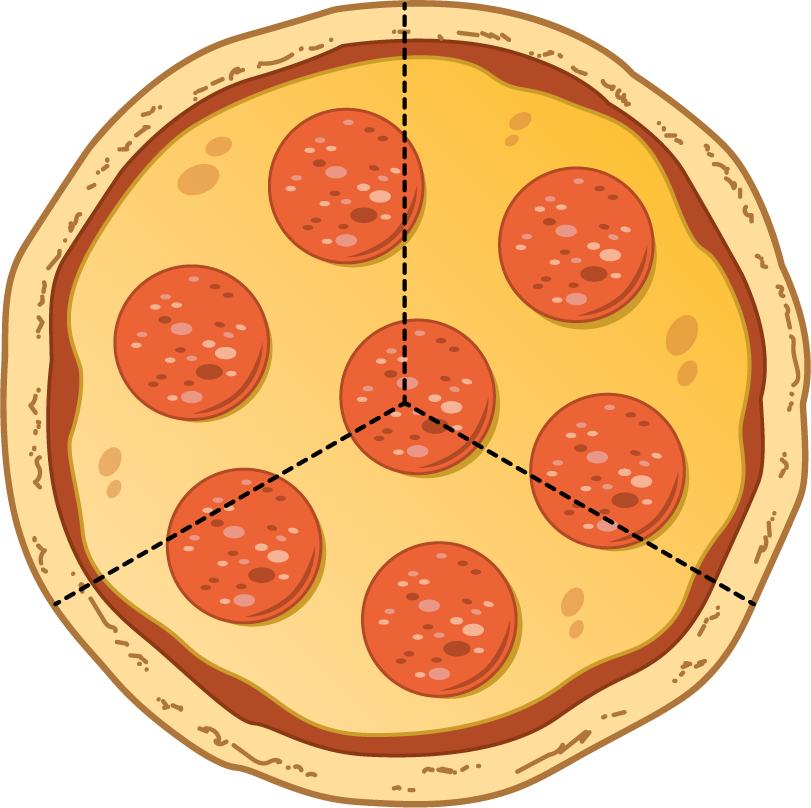
Pizza Parts

Group
Jada
Mai
- Each girl will eat ______________________ of the pizza.
- Together they will eat ________________________ of the pizza.
-
Pizza Parts
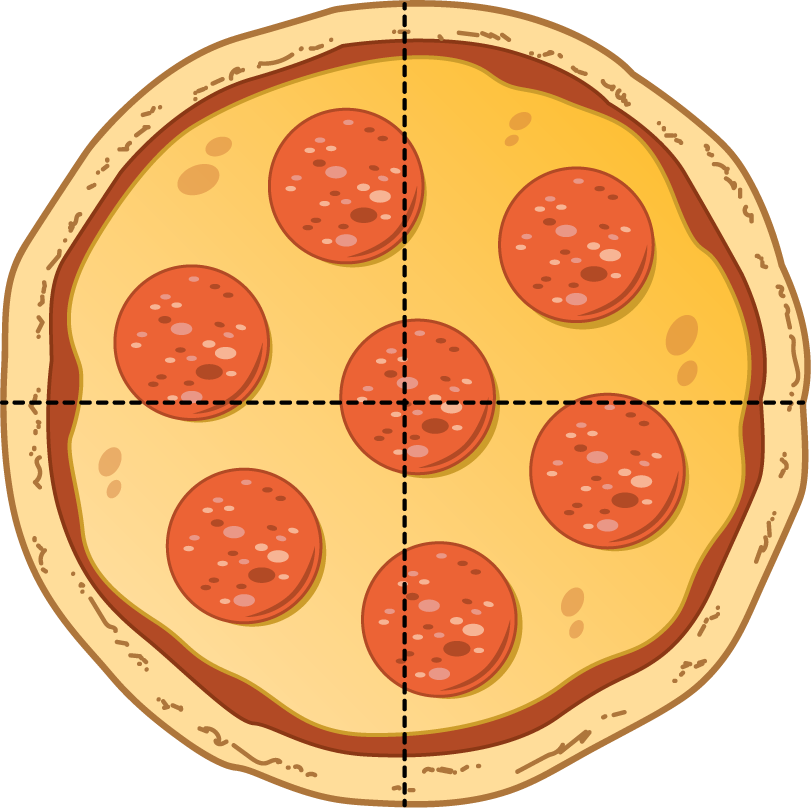
Group
Elena
Tyler
Lin
Kiran
- How much pizza will each child eat? ________________________
- How much pizza will they eat in all? ________________________
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students disagree that 2 halves, 3 thirds, or 4 fourths is the same as the whole pizza, consider asking:
- “If Jada ate this piece (one half) and Mai ate this piece (one half), how much of the pizza is left?”
- “How could you show how much of the pizza each student ate?”
Activity Synthesis
- Invite students to share how much of the pizza each group of friends ate using halves, thirds, fourths, and quarters.
- Record responses.
- “Each group had the same-size pizza. Of all the students, which group of students will have the largest slices? Why do you think that is?” (Jada and Mai only have to share the pizza with 2 people, so they have the largest pieces.)
- “What do you notice about the size of the slices and the number of students?” (The slices get smaller if there are more students.)
- Share and record responses.
Activity 2: Equal Shares of the Pie (20 minutes)
Narrative
The purpose of this activity is for students to recognize and describe pieces of circles using the words half of, a third of, and a quarter of. Students match shapes partitioned into halves and quarters to stories and partition shapes into quarters and halves based on directions. Students can continue to use one fourth when describing a piece, but encourage the use of a quarter as a way to describe the same piece.
Supports accessibility for: Visual-Spatial Processing
Required Materials
Materials to Gather
Launch
- Groups of 2
- Give students access to colored pencils.
Activity
- “You are going to read some stories with a partner about students sharing pies.”
- “Then you will partition and color shapes on your own.”
- 5 minutes: partner work time
- As students work, encourage them to use precise language when talking with their partners.
- Consider asking: “Is there another way you could say how much of the circle is shaded?"
- 10 minutes: independent work time
- Monitor for students who accurately shade the circles to share in the synthesis.
Student Facing
Write the letter of each image next to the matching story.
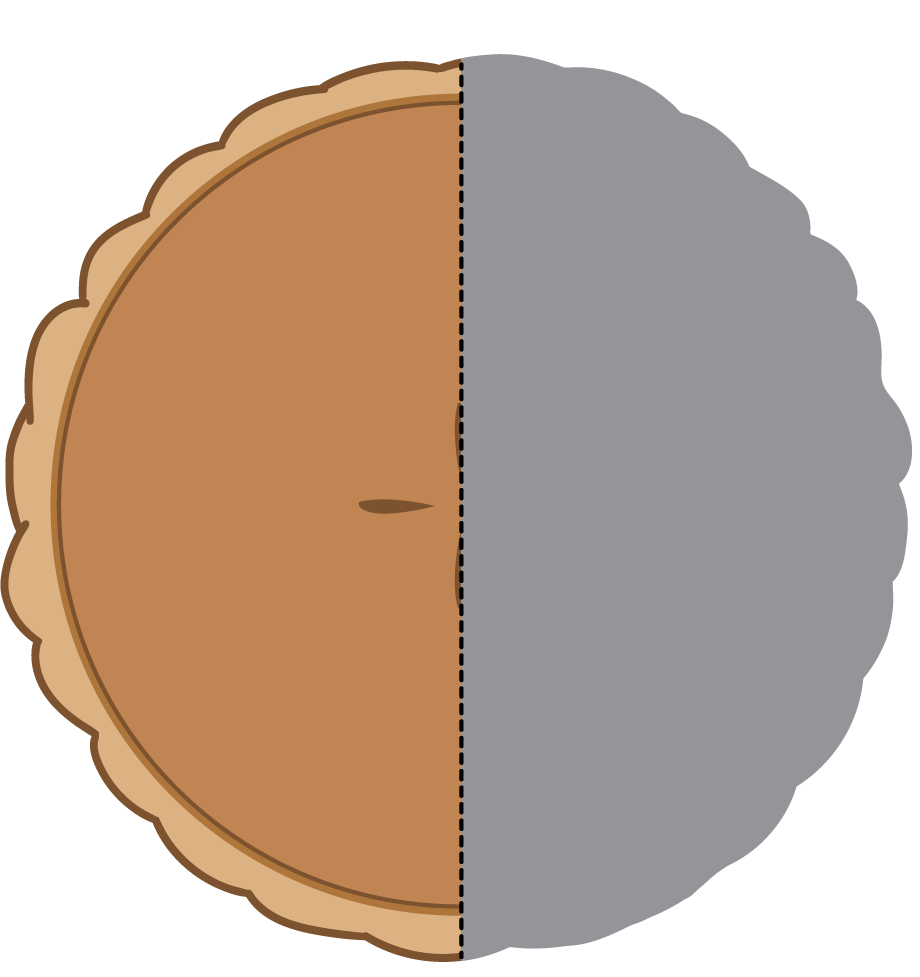


- Noah ate most of the pie. He left a quarter of the pie for Diego. __________
- Lin gave away a half of her pie and kept a half of the pie for herself. __________
- Tyler cut a pie into four equal pieces. He ate a quarter of the pie. __________
- Mai sliced the pie to share it equally with Clare and Priya. __________
- How much of the pie will they each get? a _________________
- How much of the pie will they eat in all? _________________
-
Now you try.
- Partition the circle into four equal pieces.
- Shade in a quarter of the circle red.
- Shade in the rest of the circle blue.
How much of the circle is shaded? _____________________________
-
- Partition the circle into 2 equal pieces.
- Shade one half of the circle blue.
- Color the other piece yellow.
How much of the circle is yellow? ________________________
How much of the circle is shaded? ________________________
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Invite previously selected students to display their partitioned circles. Share at least one example of a circle partitioned into halves and one example of a circle partitioned into fourths.
- “How are the circles you partitioned and shaded the same? How are they different?” (They are both circles. They are shaded with different colors. They are partitioned differently. The whole circle is shaded in both. All of the pieces are shaded in both.)
- “How much of each circle is shaded?” (4 fourths, 2 halves, the whole circle)
Lesson Synthesis
Lesson Synthesis
“We have learned a lot about composing and decomposing shapes. Sometimes different-size pieces can make up a whole shape. Sometimes the whole shape is made up of equal-size pieces. We learned that these equal-size pieces of a whole have special names.”
“Each of these shapes has pieces shaded. How would you name each one? Are there any pieces that you are not sure how to name? Explain.” (The first circle shows 2 halves because there are two equal pieces. The first hexagon has some pieces that are not thirds because each piece is a different size. I think the red trapezoid is half because you could use another trapezoid that's the same size to make the whole hexagon, but I'm not sure.)







Cool-down: Partition a Circle (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Section Summary
Student Facing
We have learned a lot about composing and decomposing shapes. Sometimes the pieces make up a whole shape, but all of the pieces are not the same size. Sometimes the whole is partitioned into equal pieces and they have special names. We practiced partitioning shapes into halves, thirds, and fourths. We learned that halves, thirds, and fourths of the same shape can look different. We learned that we can say the whole shape is 2 halves, 3 thirds, 4 fourths, or 4 quarters.
How can you use halves, thirds, fourths, or quarters to describe the pieces of these shapes? How can you use halves, thirds, fourths, or quarters to describe the whole shape?