Lesson 8
Equations on a Number Line
Warm-up: Choral Count: Back by 10 (10 minutes)
Narrative
The purpose of this Choral Count is to invite students to practice counting back by 10 from any number and notice patterns in the count. When students recognize that the digit in the ones place remains the same, while the digit in the tens place decreases by 1 each time, they look for and make use of the base ten-structure and express regularity in repeated reasoning (MP7, MP8). These understandings help students develop fluency and will be helpful later in this lesson when students show their thinking on the number line.
Launch
- “Count back by 10, starting at 99.”
- Record as students count.
- Stop counting and recording at 49.
- “Count back by 10, starting at 98.”
- Record as students count directly below the first count.
- Stop counting and recording at 48.
- “Count back by 10, starting at 95.”
- Record as students count directly below the second count.
- Stop counting and recording at 45.
Activity
- “What patterns do you see?” (The ones digit stays the same, but the tens digit goes down by one.)
- 1–2 minutes: quiet think time
- Record responses.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “Who can restate the pattern in different words?”
- “Does anyone want to add an observation on why that pattern is happening here?”
Activity 1: Represent Equations (15 minutes)
Narrative
The purpose of this activity is for students to represent addition and subtraction equations on a number line. Students consider where to begin and in which direction to draw their arrows in order to accurately represent the operation in the given equation. Throughout the activity, encourage students to explain how they know their representation matches the equation. Listen for the way they explain how they know where to start and end their arrow, which direction they draw their arrow, and how they connect the length the jump represents to the equation (MP3).
Advances:Speaking, Conversing
Launch
- Groups of 2
- “We have seen addition and subtraction equations represented on a number line. How can you tell whether a number line is representing addition or subtraction?” (Look at the direction of the arrow.)
- 30 seconds: quiet think time
- Share responses.
Activity
- “Now you are going to represent some equations on number lines. Be sure others will be able to tell from looking at your number line whether you are representing addition or subtraction.”
- 8 minutes: independent work time
- Monitor for students who:
- Mark the first number and last number in each equation with a point first. Then draw their arrow to match the operation.
- Locate the first number in the equation, count a number of spaces forward or backward to match the operation, and draw an arrow to connect the two numbers.
- “Compare your number lines with your partner. Explain how you know your representation matches the equation.”
- 3 minutes: partner discussion
Student Facing
Represent each equation on the number line.
-
\(15 + 7 = 22\)
-
\(18 - 6 = 12\)
-
\(46 + 7 = 53\)
-
\(33 - 9 = 24\)
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
- “Will you please explain your representation?”
- “How did you decide where to start or end on the number line?”
- “How did you decide which direction to draw your arrow?”
Activity Synthesis
- Display the equation and blank number line for \(15 + 7 = 22\).
- Invite previously selected students to share how they represented the equation on the number line.
- Consider asking:
- “How do you see each number in the equation in ____’s representation?”
- “How do you know ___’s representation matches the operation (addition or subtraction)?”
- As time permits, continue with the other equations.
Activity 2: Write Equations (20 minutes)
Narrative
The purpose of this activity is for students to write addition and subtraction equations to match number line representations. Students determine the operation represented by looking at the direction of the arrows. They identify the starting number, the length of the jump, and the ending number in order to write the equation. Each representation shows a relationship between the same three numbers. When students explain to each other why they think two representations are most alike, they look for and make sense of the structure of the number line and deepen their understanding of the relationship between addition and subtraction (MP3, MP7).
Supports accessibility for: Conceptual Processing, Attention
Launch
- Groups of 2
Activity
- “Now you are going to look at number lines and write equations that match the diagram.“
- 5 minutes: independent work time
- “Compare your equations with your partner. Take turns explaining how your equation matches the number line diagram.”
- “Then work together to choose two number lines that you think are the most alike. Be prepared to explain your choice.”
- 5 minutes: partner discussion
- Monitor for students who:
- explain how their equation matches the point, direction of the arrow, final position of the arrow, and the length of the movement on the number line
- discuss how number lines are the same because they show the same operation
- discuss how number lines are the same because the length of the jump is the same
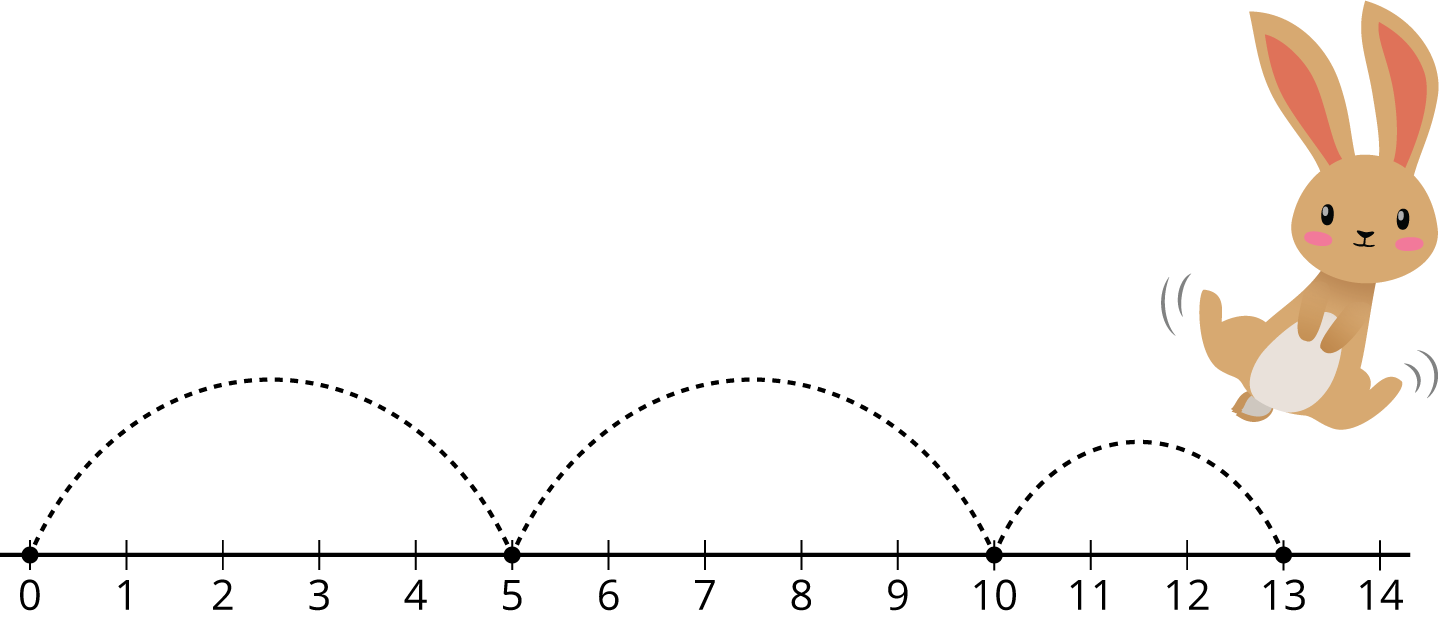
Student Facing
For each number line, write an equation that matches the diagram.
-
Equation:__________________________
-
Equation:__________________________
-
Equation:__________________________
-
Equation:__________________________
- Compare your equations with your partner.
- Pick the 2 number lines you think are most alike. Explain your choice to your partner.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
- “How do you see each number in the diagram?”
- “How does your equation match the arrow in the diagram?”
- “Why does your equation start with __? Where is that number in the diagram?”
- “Which number in your equation represents the length between __ and __?”
Activity Synthesis
- Invite previously identified students to share their equations for each number line.
- Consider asking:
- “Do you agree or disagree? Explain.”
- “Can anyone explain why ___’s equation matches the number line in another way?”
- Invite previously identified students to share the number lines they feel are most alike.
- If time, ask “In what other ways are the number lines alike? How are they different?”
Lesson Synthesis
Lesson Synthesis
“Today we worked with equations and number line representations.”
“How could you explain to a friend how they could use the number line to show addition and subtraction?” (You can use an arrow to show moving from one spot to another on the number line. Moving right is like adding. Moving to the left is like subtracting. You can use a point to show where you start and the arrow shows where you end.)
Cool-down: Represent Addition and Subtraction on the Number Line (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.







