Lesson 9

The purpose of this warm-up is to elicit the idea that teen numbers can be represented with different tools, which will be useful when students build teen numbers on 10-frames in a later activity. While students may notice and wonder many things about these images, seeing the tower of 10 and the full 10-frame as a unit is an important discussion point.

• Groups of 2
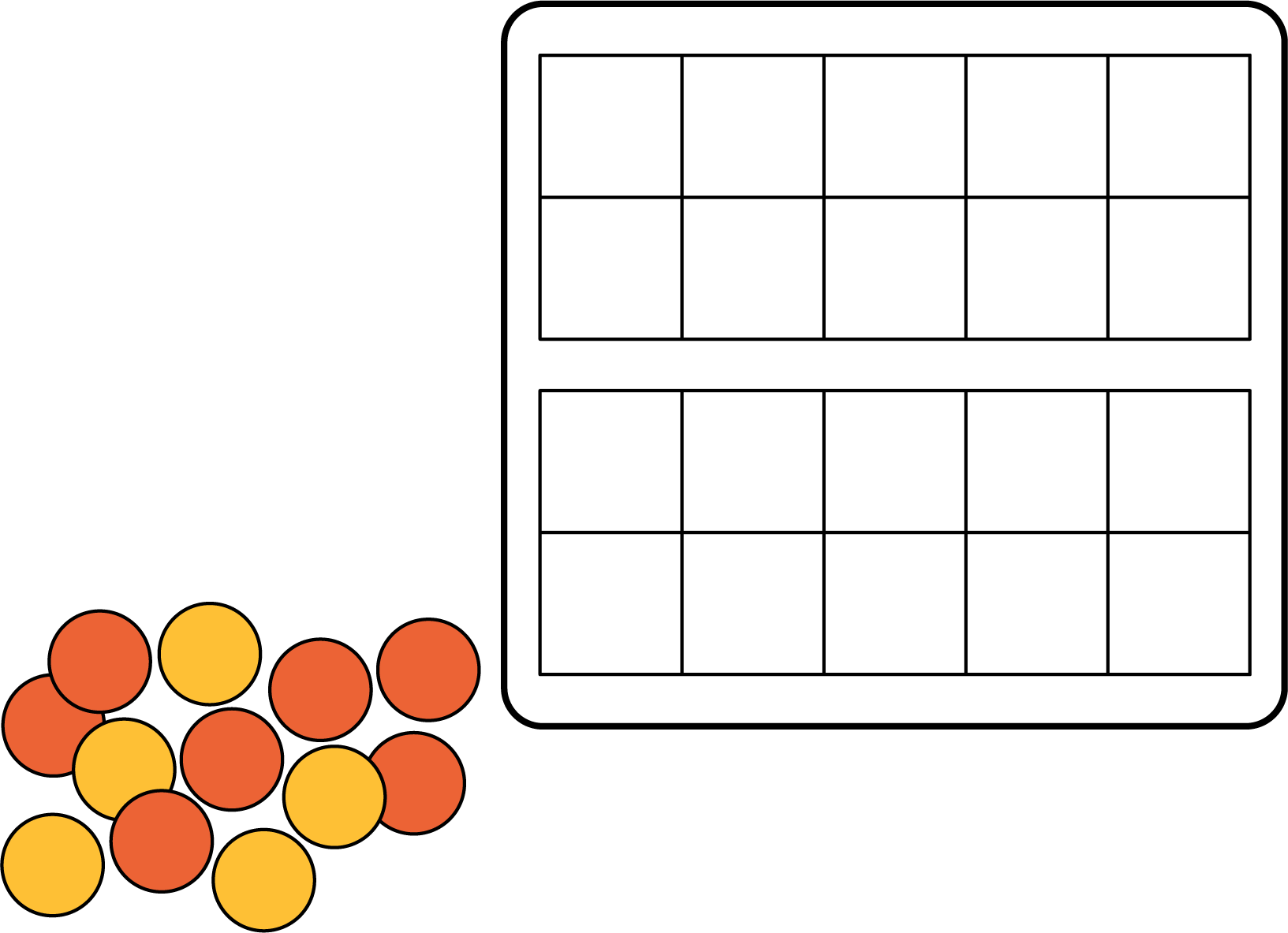
• Display the image.
• “What do you notice? What do you wonder?”
• 1 minute: quiet think time

• “Discuss your thinking with your partner.”
• 1 minute: partner discussion
• Share and record responses.

• “How could you figure out how many objects there are in each image?” (I saw that one whole 10-frame was filled, so I knew that was 10. Then I counted on. I saw that the connecting cubes were in a tower of 10 and then there were some more left over. I could count all the objects in the image.)

The purpose of this activity is for students to continue to explore teen numbers as 1 ten and some ones, using a new version of a familiar tool, the double 10-frame. Students choose a teen number and build it. As they build teen numbers, students should notice that every teen number has a completed 10-frame. or 1 ten, in common. This further solidifies student understanding that all teen numbers have 1 ten. Some students may build the teen number, counter by counter, each time. These students are still developing an understanding of 10 ones as 1 ten. Some students may realize that one of the 10-frames is always completely filled and only change the ones. When students notice the relationship between teen numbers and the 10 + n pattern, they look for and make use of structure (MP7). Students who leave one 10-frame full and change the counters in the other 10-frame are observing regularity in how the teen numbers are formed (MP8).

Double 10-Frames are provided as a blackline master. Students will continue to use these throughout the year. Consider copying them on cardstock or laminating them and keeping them organized to be used repeatedly.

• Create a set of Number Cards (11-20)  from the blackline master for each group of 2.

• Groups of 2
• Give each group a set of cards, a double 10-frame, and access to at least 20 connecting cubes or two-color counters.
• “We’re going to use our double 10-frames to build teen numbers today. Let's do one together.”
• Choose a card.
• “What number is on my card? Let's build that number on the double 10-frame.”
• Demonstrate building the teen number.
• “Now we write an equation to show how we built the number.”
• Write an equation such as 10 + 4 = 14.

• “Now you will build more teen numbers with your partner. Make sure you both agree on how to build the number and what equation to write.”
• 10 minutes: partner work time
• Monitor for students who:
  • build a new ten each time
  • count the 10 each time
  • change the ones only

If students remove all counters from the 10-frames and build a new ten for each teen number, consider asking:

• “Can you explain how you built this number?”
• “Can you keep some of the counters here to help you build your next number?”

• “When you were building these numbers, what part of the equation was the same? What part was different?” (There was always 10 in each equation. I was adding each time. The total changed and was always a teen number. The number I was adding to 10 changed.)

The purpose of this activity is for students to determine the value that makes addition equations true. The numbers in the equations all use the relationship between 1 ten and some ones and teen numbers. Students find the value that makes the equation true with one addend or the total unknown. This will help when students solve story problems with the unknown value in different positions in a later lesson.

• Groups of 2
• Give students access to double 10-frames and connecting cubes or two-color counters.

• Read the task statement.
• 6 minutes: independent work time
• 4 minutes: partner discussion

• “How are the last two problems related?” (They both show that 13 is the same as 10 and 3. 13 is the sum but they have different missing values.)