The big ideas in grade 1 include: developing understanding of addition, subtraction, and strategies for addition and subtraction within 20; developing understanding of whole-number relationships and place value, including grouping in tens and ones; developing understanding of linear measurement and measuring lengths as iterating length units; and reasoning about attributes of, and composing and decomposing geometric shapes.

The mathematical work for grade 1 is partitioned into 8 units:

1. Adding, Subtracting, and Working with Data
2. Addition and Subtraction Story Problems
3. Adding and Subtracting within 20
4. Numbers to 99
5. Adding within 100
6. Length Measurements within 120 units
7. Geometry and Time
8. Putting it All Together

In these materials, particularly in units that focus on addition and subtraction, teachers will find terms that refer to problem types, such as Add To, Take From, Put Together or Take Apart, Compare, Result Unknown, and so on. These problem types are based on common addition and subtraction situations, as outlined in Table 1 of the Mathematics Glossary section of the Common Core State Standards.

In this unit, students deepen their understanding of addition and subtraction within 10, and extend what they know about organizing objects into categories and representing the quantities.

In kindergarten, students solved addition and subtraction word problems within 10 using objects and drawings. They learned about Put-Together, Result-Unknown problems and worked toward fluency with sums and differences within 5.

The activities in this unit reinforce these understandings and initiate the year-long work of developing fluency with sums and differences within 10. Some problems involve finding sums greater than 10, a skill to be honed throughout the course and with the support of tools such as connecting cubes.

Students also build on the work in kindergarten as they engage with data. Previously, they sorted objects into given categories such as size or shape.  Here, students use drawings, symbols, tally marks, and numbers to represent categorical data. They go further by choosing their own categories, interpreting representations with up to three categories, and asking and answering questions about the data.

This opening unit also offers teachers opportunities to introduce mathematical routines and structures for centers, and to develop a shared understanding of what it means to do math and to be a part of a mathematical community.

Number Race

Five in a Row

Find the Pair

Check It Off

In this section, students engage with addition and subtraction within 10 through activities and centers. The work here allows teachers to assess students’ understanding of addition and subtraction, as well as their fluency with facts within 5, a kindergarten goal.

There is an emphasis on adding and subtracting 1 or 2 to encourage students to count on or count back, which helps to build their awareness of how addition and subtraction relates to counting. To support this development, give students access to two-color counters and 10-frames throughout this section.

In this section, students organize and represent data. They begin by sorting objects into categories of their choice, describing their categories, and counting the number of objects in each category.

Next, students learn to collect data by conducting a survey. No specific data representations are required in grade 1, so students record and organize data in a way that makes sense to them. They may represent the results using objects, symbols, tally marks, or numbers. Students then make sense of one another’s representations (MP1).

The focus of this section is on interpreting data represented in different ways and on asking and answering questions about them.

Students analyze representations of data and respond to “how many in each category” and “how many in all” questions. They consider which representation (tallies or numbers) is most helpful in answering certain types of questions. They also think about questions that could be asked given a representation of data.

Students begin responding to written questions in this section. To support students with the reading demand, consider reading the questions aloud or arranging students to work with a partner.

In this unit, students learn to solve new types of addition and subtraction story problems and relate the quantities in the stories to equations.

In kindergarten, students solved a limited number of types of story problems within 10 (Add To/Take From, Result Unknown, and Put Together/Take Apart, Total Unknown, and Both Addends Unknown). They represented their thinking using objects, fingers, mental images, and drawings. Students saw equations and may have used them to represent their thinking, but were not required to do so.

Here, students encounter most of the problem types introduced in grade 1: Add to/Take From, Change Unknown, Put Together/Take Apart, Unknowns in All Positions, and Compare, Difference Unknown. The numbers are kept within 10 so students can focus on interpreting each problem and the relationship between counting and addition and subtraction. This also allows students to continue developing fluency with addition and subtraction within 10.

As they solve problems, students analyze and write equations and consider the meaning of the equal sign. They may initially see it as a prompt for the answer to a question, which makes it difficult to interpret equations such as \(7=5+2\). Developing an understanding of the equal sign is particularly important in solving missing-addend problems. For example:
 

There are 9 counters total.
How many counters are under the cup?

Students may see a subtraction problem, represented by \(9-4=\boxed{5}\), or a missing-addend problem, represented by \(4 +\boxed{5} = 9\). This work also highlights that multiple equations can often be written for each story problem.

It is more important for students to explain the relationship between the equation they wrote and the story, than for their equations to match the story or their solution method.

To help students think about the meaning of each number in an equation, a box is placed around the answer to the question in the problem. In the last section, students work with equations where an empty box represents the unknown.

In the next unit, students will solve addition and subtraction problems within 20 and work with equations with a symbol for the unknown in all positions, and further develop their fluency within 10. 

In this section, students revisit familiar problem types (Add To and Take From) where they can physically act out the problems with objects or drawings. They work formally with equations for the first time, writing addition and subtraction equations that match story problems. They write equations such as \(2 + 7 =\boxed{9}\) and learn the convention of drawing a box around the answer to the question in the story problem.

Students also work with Add To, Change Unknown problems for the first time. In writing equations to match these problems, students see that the answer to the question doesn’t necessarily come after the equal sign. For example:

Students solve this problem by counting on from 6 to 8 and write the equation \(6 + \boxed{2} = 8\) to represent the story. Students come to see counting on as a way to solve Add To, Change Unknown problems.

In this section, students solve Put Together/Take Apart problems in which the total, one addend, or both addends are unknown. This builds on work from kindergarten when students composed numbers up to 10 in different ways.

Students consider problems in the context of Shake and Spill, a game that uses two-color counters. For example:

Elena is playing Shake and Spill. She has 7 counters.
What are some ways to show some red and some yellow?

This problem type enables students to see the same situation represented by different equations, such as those where the total is written before the equal sign (\(7=4+3\)) and those illustrating the commutative property (\(4+3=7\) and \(3+4=7\)). When students analyze and connect quantities in story problems with the structure of equations, they are thinking quantitatively and abstractly (MP2). 

Note that students do not need to use the terms “commutative property” or “associative property.” These are referred to as the “add in any order” property.

In this section, students solve Compare, Difference Unknown problems, reinforcing their understanding of the relationship between addition and subtraction.

Students begin by considering how many to add to a quantity to make the two quantities equal, such as, "How many cubes do we need to add so that both towers have the same number of cubes?"

Once they are familiar with this language, students answer “how many more” and “how many fewer” questions. For example, "How many more cubes does Clare have than Andre?"

In this case, students may count the extra cubes in Clare’s tower to find the answer. They may start at 3 and count up to 10 or start at 10 and count back to 3. Students analyze both addition (\(3+7=10\)) and subtraction (\(10-3=7\)) equations that can be used to represent the same problem.

When students reason about questions, quantities, and relationships in story problems and write equations to represent them, they make sense of problems to solve them (MP1) and reason quantitatively and abstractly (MP2).

In this section, students bring together the work of the unit to solve and compare a variety of problem types, write equations to represent problems, and make sense of equations with a symbol for the unknown. (They are not required to use symbols in the equations they write.) Students also reason in the other direction: writing stories and questions that correspond to given equations, and using drawings, numbers, and words to find the answers. 

In this unit, students develop an understanding of 10 ones as a unit called “a ten” and use the structure of \(10 + n\) to add and subtract within 20.

In kindergarten, students composed and decomposed the numbers 11–19 into 10 ones and some more ones. In a previous unit, students solved story problems of all types with unknown values in all positions and numbers within 10. They used the relationship between addition and subtraction, drawings and equations, and various tools (10-frames, connecting cubes, two-color counters) to represent the quantities in the problems. They learned that the values represented by the numbers or expressions on each side of an equation are equal.

Here, students decompose and recompose addends to find the sum of two or three numbers. For example, to find the value of \(9 + 6\), they may decompose 6 into 1 and 5, compose the 1 and 9 into 10, and find \(10 + 5\).

Subtraction work occurs throughout the unit and becomes the focus in the last section. Students consider taking away and counting on as methods for subtracting. They understand subtraction as an unknown-addend problem and use their knowledge of addition to find the difference of two numbers.

For instance, students may reason about the value of \(10-6\) by:

Taking away 6 from 10

Counting on to 10, starting from 6

Using an addition fact, \(6 + 4 = 10\)

Students solve story problems throughout the unit and learn two new problem types—Add To, Start Unknown and Take From, Change Unknown. Students compare the structure of different types of story problems as they practice adding and subtracting within 20.

This section focuses on developing students’ fluency with addition and subtraction within 10. All but a few sums within 10 can be found by counting on by 1, 2, or 3, or by making a sum of 10, so being able to count on up to 3 and make 10 are helpful steps toward fluency. Students have a chance to self-assess the sums they know from memory and those they are still working on. (Fluency is not expected until the end of the school year).

Note that the term “sum” has so far been used to refer to a number—the total we have when adding two or more numbers. Here, the term is also used to refer to an addition expression like \(5 + 4\) because it represents the sum of two quantities.

The 10-frame can help students visualize sums of 10. For example, this 10-frame may allow students to recall several related facts:

\(8 + 2 = 10\)
\(2 + 8 = 10\)
\(10 - 2 = 8\)
\(10 - 8 = 2\)

Changing one counter from red to yellow illustrates \(7 + 3 = 10\), and changing a counter from yellow to red illustrates \(9 + 1 = 10\). Seeing ways to make 10 will support students in later work of adding and subtracting within 20 and within 100.

Students are introduced to Add To, Start Unknown story problems. Because the starting number is unknown, students may find this challenging. Encourage them to act out the stories and apply what they have learned about adding within 10 to solve these problems.

In this section, students begin exploring the structure of the base-ten system and the idea of place value as they work with teen numbers. 

Students see that a new unit, a ten, is composed from 10 ones, and that teen numbers are composed of 1 unit of ten plus some number of ones. Double 10-frames are used here as they encourage students to see this structure (MP7).

Unlike in connecting cube towers, where identifying a unit of ten means counting individual cubes, the unit of ten—and whether it is complete—is evident in double 10-frames.

The structure of teen numbers and double 10-frames help students add and subtract teen numbers.

Here students work only with expressions that do not require composing or decomposing a ten, for example, \(13-2\) and \(12+5\). They notice that the unit of ten doesn’t change and relate the sum to the adding or subtracting of ones.

Students encounter a new problem type—Take From, Change Unknown—in which the number that needs to be subtracted to get a difference is unknown. Encourage students to act out the story problems or to use double 10-frames and counters to make sense of them. 

While they are not expected to write equations that match the action in a story, students do write equations that they may use to solve problems and explain how their equations relate to the stories. In doing so, they reason quantitatively and abstractly (MP2). 

In this section, students explore the idea of composing and decomposing numbers to add up to three addends within 20. They make use of the base-ten structure and the commutative and associative properties (collectively referred to as the “add in any order” property throughout the materials) when adding, and discover the usefulness of grouping numbers to make a sum of 10 (or a unit of ten). 

For instance, to find the value of \(4 + 7 + 6\), they can rearrange the addends to group 4 and 6, which makes 10, and add the 7.

\(\hspace{2cm}\)
\(4 + 7 + 6\)
\(4 + 6 + 7\)
\(10 + 7\)
17

Making a ten is also helpful when finding the sum of two addends. For example, to find the value of \(9 + 5\), students can take 1 from the 5 and group it with the 9 to make 10, and then add the 4.

\(\hspace{2cm}\)
\(9 + 5\)
\(9 + 1 + 4\)
\(10 + 4\)
14

Although this section focuses on making a ten, students may use other facts they know to find sums. For example, given \(7 + 8\), students who know the value of \(7 + 7\) may think of it as \(7 + 7 + 1\).

In this section, students subtract within 20. They rely on the relationship between addition and subtraction and the idea of making a ten to do so. Students encounter subtraction expressions and missing-addend equations, and use taking-away and counting-on methods to find differences. 

For example, given \(15  - 8\), students may take away 5 to get to 10 and then take away another 3 to find the difference of 7.

\(\hspace{2cm}\)
\(15 - 5 = 10 \)
\(10 - 3 = 7\)

They may also start with 8 and count on by 2 to get 10, and then add another 5 to reach 15.  They see that the difference is 7.

\(\hspace{2cm}\)
\(8 + 2 = 10 \)
\(10 + 5 = 15\)
\(2 + 5 = 7\)

This unit develops students’ understanding of the structure of numbers in base ten, allowing them to see that the two digits of a two-digit number represent how many tens and ones there are.

Previously, students counted forward by one and ten within 100 in the Choral Counting routine. They learned that 10 ones make a unit called a ten and that a teen number is a ten and some ones.

Here, as they count and group quantities, students generalize the structure of two-digit numbers in terms of the number of tens and ones. This understanding enables students to transition from counting by one to counting by ten and then counting on. For example, to count to 73, they may count 7 tens and count on—71, 72, 73. 

Students interpret and use multiple representations of two-digit numbers: connecting cubes, base-ten diagrams, words, and expressions. Connecting cubes in towers of 10 and singles are used instead of base-ten blocks, which will be used in later grades, so units of ten can be physically composed and decomposed with the cubes. Here are some representations for 73:

7 tens and 3 ones
3 ones and 7 tens

\(70 + 3\)
\(63 + 10\)
\(60 + 13\)

Students also represent two-digit numbers with their own drawings. They may start by drawing towers of ten and show each unit of one within each ten, and later simplify their drawings to show rectangles for tens and small squares for ones. Encourage students to use the drawings that make sense to them, and for those who create the more abstract drawing, to express how many ones each ten represents.

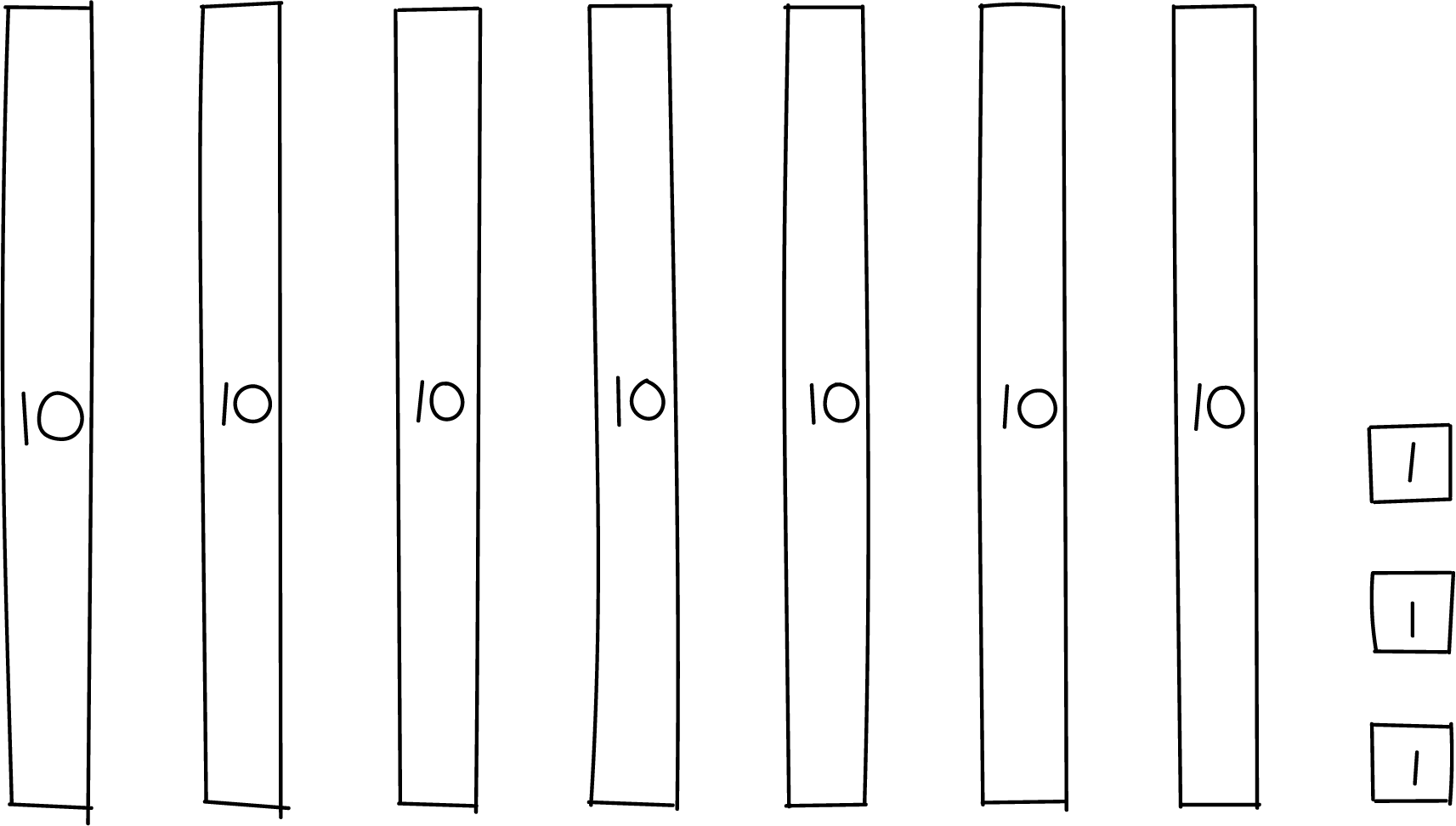
To help students make sense of base-ten representations, give students access to connecting cubes—towers of 10 and singles —in all lessons. Some students may also benefit from access to double 10-frames and two-color counters, however all students should be encouraged to work toward using connecting cubes in towers of 10 and singles. 

Later in the unit, students use the value of the digits to compare two-digit numbers and learn to use comparison symbols (<, >) to record their comparisons. The unit concludes with opportunities for students to explore different ways of using tens and ones to represent two-digit numbers.

Previously, students used a 10-frame to represent a unit of ten. In this section, they make sense of other representations of units of ten—towers of 10 connecting cubes, base-ten drawings, words, and numbers—to build an intuition for the base-ten system.

Students count collections with a multiple of 10 objects in each. As they represent the quantity in each collection, they see that counting by one and counting by ten yields the same number.

Students learn that each name and numeral used to skip-count by 10 represents an amount of tens, so 30 represents 3 tens, 40 represents 4 tens, and so on. This understanding then helps students see, for instance, that 3 tens and 2 tens is 5 tens, and to add and subtract multiples of tens.

4 tens and 1 ten is 5 tens.
\(40 + 10 = 50\)

5 tens take away 2 tens is 3 tens.
\(50 - 20 = 30\)

Because the focus here is on connecting written numbers to their word names and the amounts of tens they represent, terms such as “two-digit number,” “digits,” “multiples,” “tens place,” and “ones place” are not used. “Multiple of 10” is used in teacher-facing text, but is not a term that students use until grade 3. Students should be encouraged to use any language that makes sense to them.

In this section, students learn that the two digits in a two-digit number represent amounts of tens and ones. They begin by counting collections of objects that do not contain a multiple of 10 and express the quantity in a way that makes sense to them. Their understanding of teen numbers helps them see the collections in terms of tens and ones.

To make sense of the digits in two-digit numbers, students continue to use familiar representations such as connecting cubes and base-ten drawings, including drawings that use long rectangles to represent the tens and smaller squares to represent the ones. Students also begin to use words such as “___ tens ___ ones.”

Students then interpret addition expressions that show the value of each digit in two-digit numbers. To highlight the meaning of the digits, the expressions are shown in expanded form (30 + 5) and with the value of the ones before the tens (5 + 30).

Later in the section, students use their understanding of two-digit numbers to add multiples of ten to any two-digit number and mentally find 10 more or 10 less than any number.

In this section, students use their understanding of the base-ten structure to compare and order numbers to 99. They notice that if a two-digit number has more tens it will be greater than another number with fewer tens, no matter how many ones there are. They then generalize this insight to compare numbers based on the digits. 

The < and > symbols are introduced here. Before using the symbols to write true comparison statements, students gain familiarity by reading and interpreting statements with these symbols. They have opportunities to work with the symbols throughout the section.

\(17 < 35\)
17 is less than 35.

\(35>17\)
35 is greater than 17.

The lesson activities intentionally use mathematical language to support students in recalling how to read or write the symbols. For example, initially students are encouraged to notice that the side of the symbol with the greater amount of space between the top and the bottom segments faces the greater number. Avoid using non-mathematical or imaginative language that may distract from the focus of the unit and delay fluency with reading and writing the symbols.

In this section, students deepen their understanding of the base-ten structure by representing two-digit numbers with different amounts of tens and ones. They also extend their comparison work by comparing numbers expressed in different ways.

Students begin by making a number with towers of 10 and singles, using more than 9 single cubes. This prompts students to consider how to represent numbers in different ways, for instance, by composing a ten from 10 ones, or decomposing a ten into 10 ones.

3 tens 2 ones

2 tens 12 ones

Next, students use the symbols <, >, or = to compare numbers that are represented with different compositions of tens and ones.

The reasoning here helps prepare students to use their understanding of place value and the properties of operations as methods to add within 100.

In this unit, students add within 100, using place value and properties of operations in their reasoning.

Previously, students composed, decomposed, and compared numbers within 100. They reasoned about units of tens and ones and represented numbers with connecting cubes, base-ten drawings, expressions, and equations in different ways (for example, \(65 = 60+5\) and \(65 = 50 + 15\)). Here, they build on these understandings of place value to find sums.

Students begin by adding a two-digit number with another two-digit number or with a one-digit number where it is not necessary to compose a new ten. Then, they observe cases in which adding some ones together require composing a new ten.

Two broad methods for finding sums are explored: adding on by place (adding on tens, then ones), and adding units by place (combining tens with tens and ones with ones).

Along the way, they also compare methods from earlier work, such as counting on and making use of known sums, including sums of 10.

\(23+45\)
Add on tens, then add on ones:

To make sense of methods for adding (especially as it relates to composing a ten when adding ones and ones), students work with a variety of representations—connecting cubes in towers of 10 and singles, base-ten drawings, expressions, and equations. They also use different representations to share their thinking with others.

Expressions and equations are presented horizontally here to encourage students to make sense of the numbers and ways of adding rather than apply an algorithm. Eventually, they write equations to represent their thinking. For example, to find the sum of \(52+46\) , they might write:

Students are not expected to write or use equations in any specific way. Even in activities that focus on interpreting and writing equations, students should have continued access to drawings and other tools for sense making. Provide access to connecting cubes in towers of 10 and singles throughout the unit.

In this section, students add a two-digit number and a one- or two-digit number without composing a ten. They build on the work of prior units, in which they added one-digit numbers and teen numbers without composing a ten, and added multiples of 10 to two-digit numbers. Here, students see that when adding two-digit numbers they can add like units: tens and tens, and ones and ones.

When adding, students may use connecting cubes or drawings to show the grouping of tens and of ones and to compose a new unit of ten. They are encouraged to explain, connect, and compare their methods for finding the value of sums. Monitor for the language students use to describe their methods and emphasize vocabulary related to place value. Give students opportunities to revise their explanations and add to their representations for clarity and precision (MP6). 

At the end of the section, students write equations to represent their thinking. They may write a single equation that shows the sum (\(52 + 46 = 98\)) or they may write a series of equations to represent how they solved the problem (\(50 + 40 = 90\), \(2 + 6 = 8\), \(90 + 8 = 98\)).
 

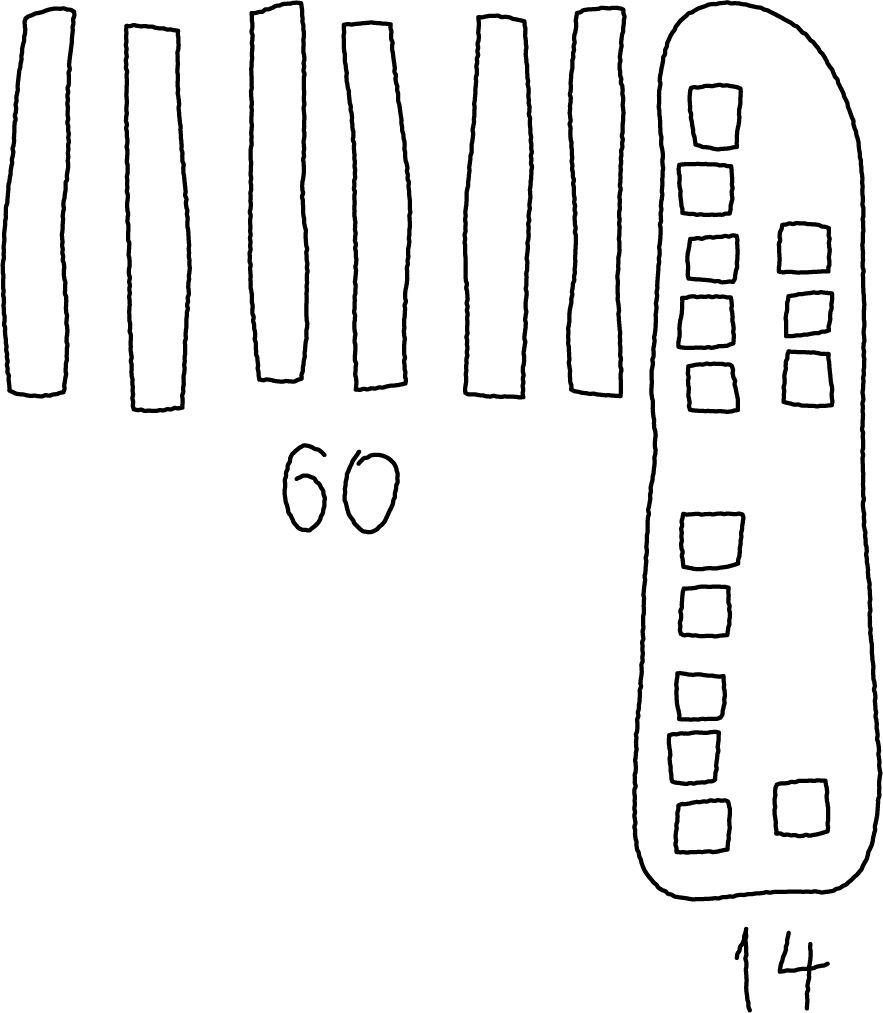
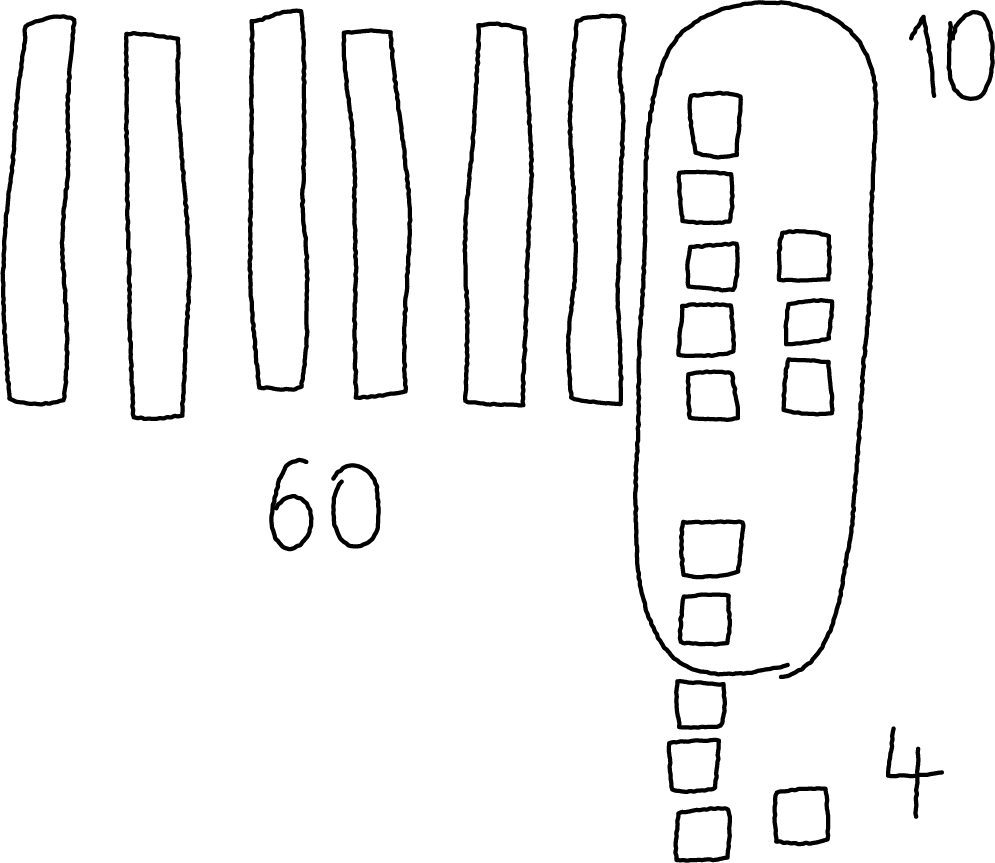
Here are 2 drawings students made for \(63+25\).

Elena's work

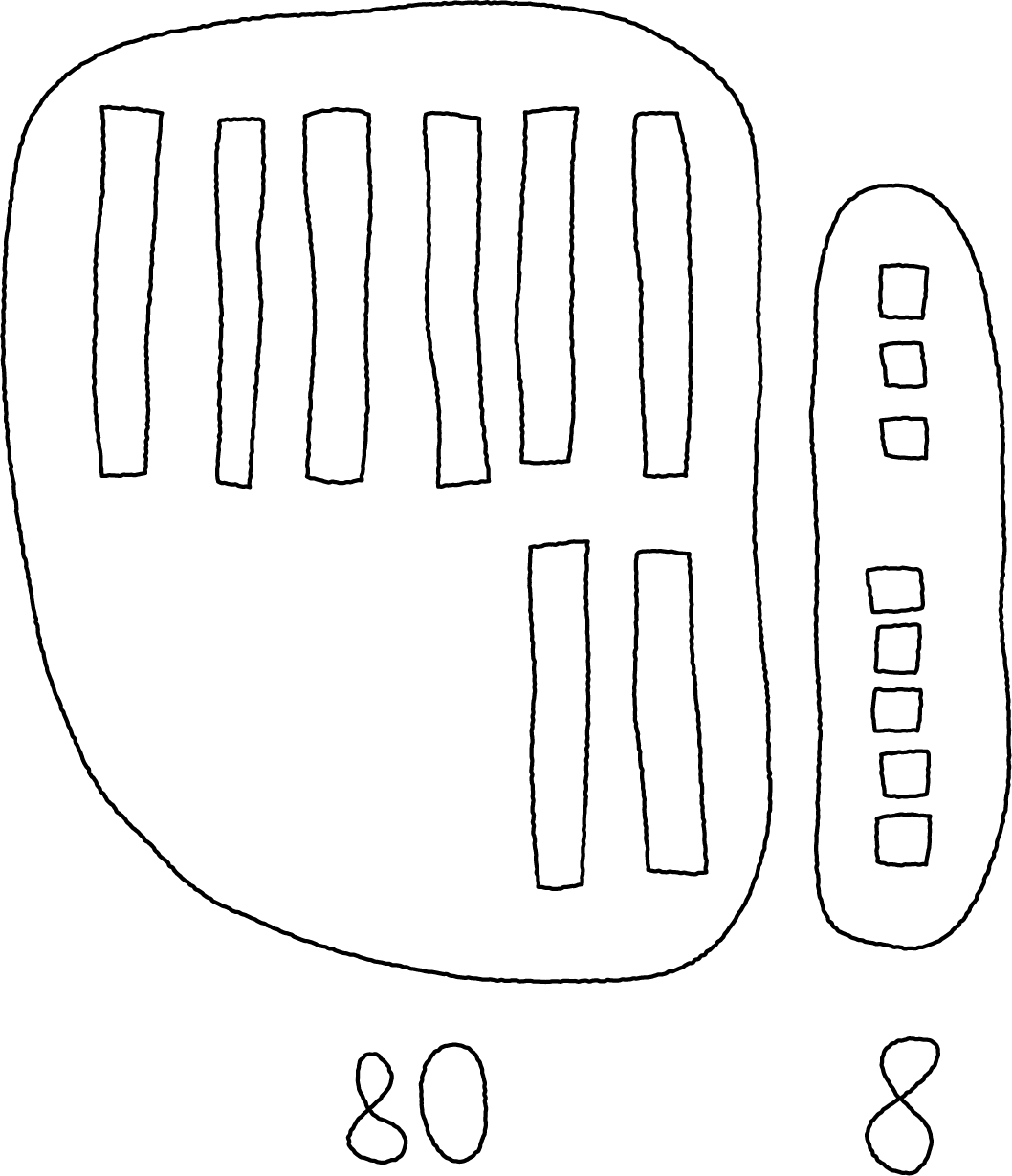
Andre's work

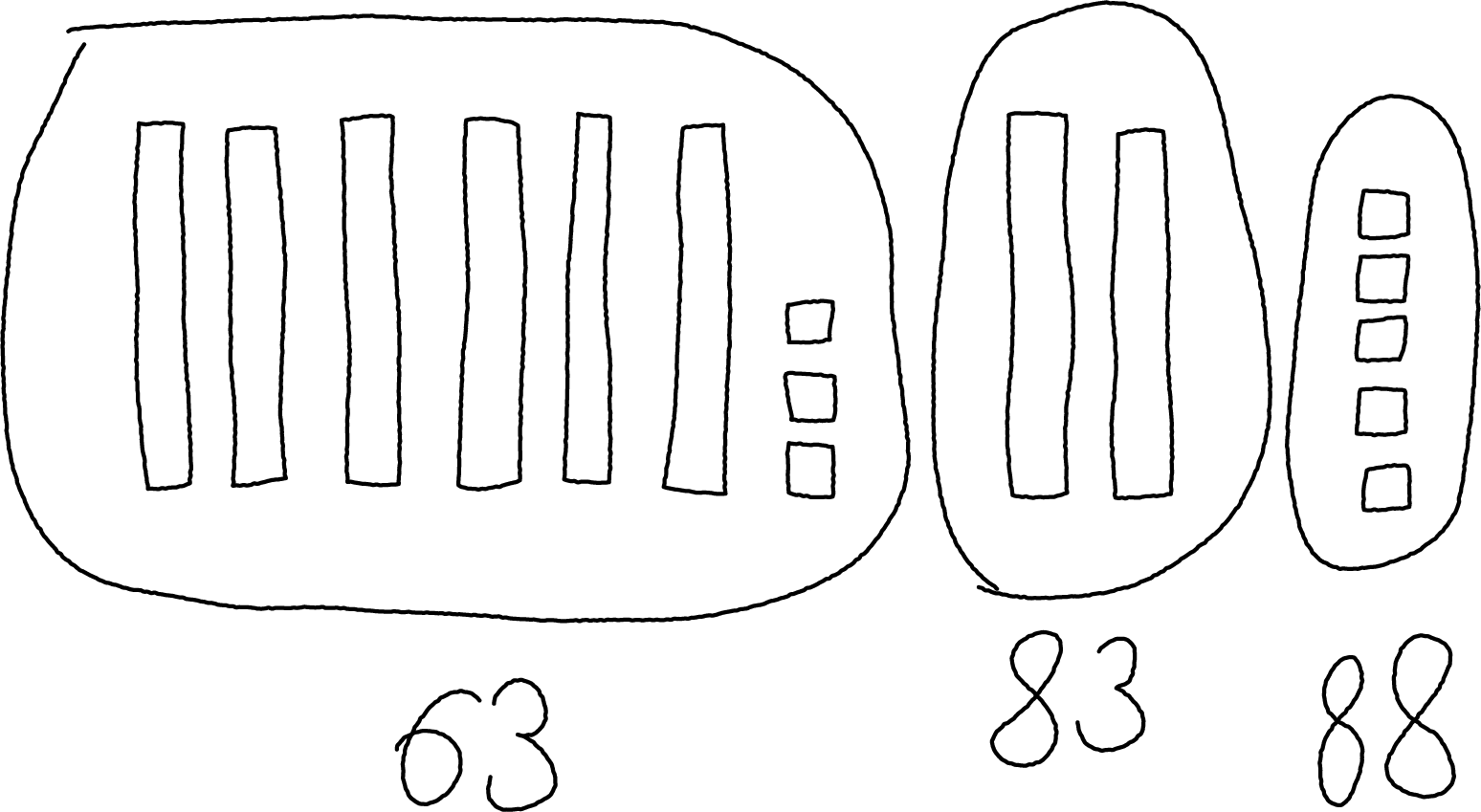
Which equations go with
which drawing?

Set A

\(63+ 20 = 83\)
​​\(83 + 5 = 88\)

Set B

\(60 + 20 = 80\)
​​\(3 + 5 = 8\)
\(80 + 8 = 88\)

In this section, students learn that sometimes when adding two-digit numbers within 100, it is necessary to compose a ten from ones. They draw on the idea of making a ten, which they learned when adding ones and when adding numbers within 20.

Students may not initially consider composing a new unit of ten when adding numbers. They may count on by ones, or count on by place (count on by tens and by ones separately). They may also count on to the next ten, but not connect their counting to a new unit of ten.

Counting on:
68, 69, 70, 74

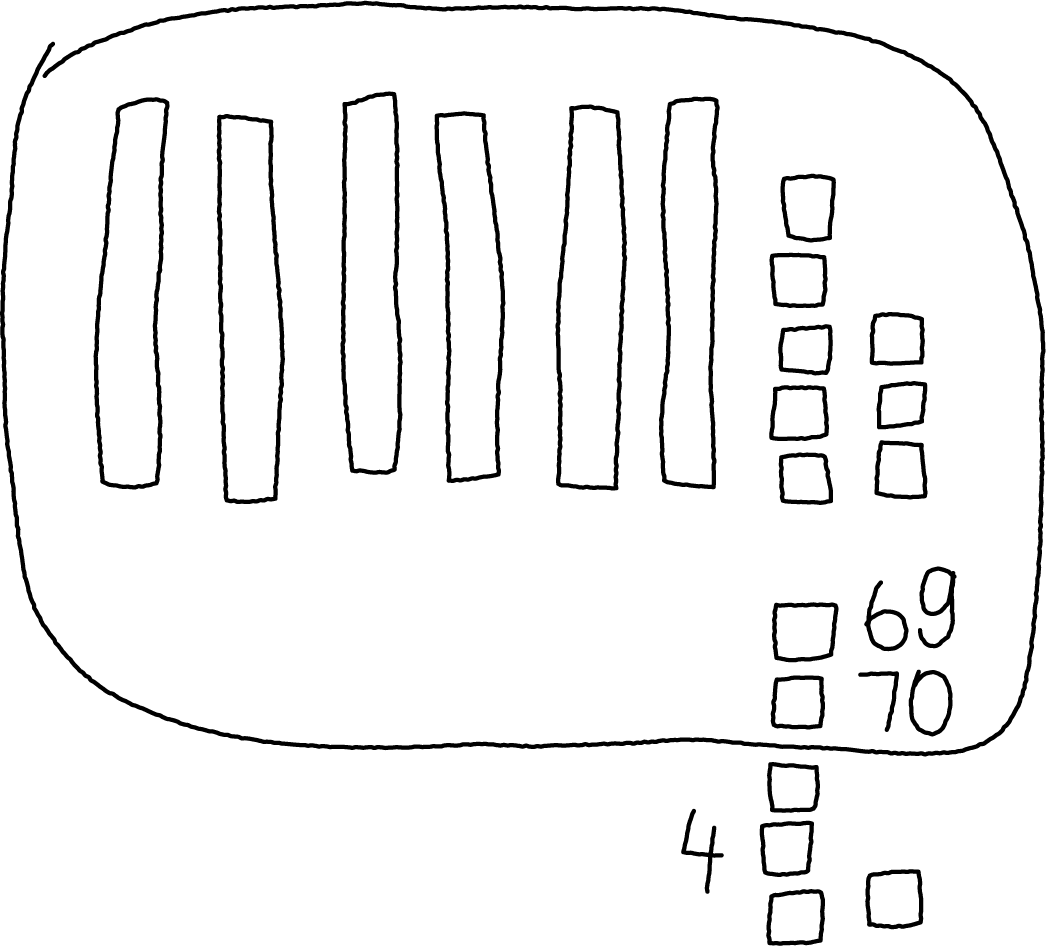
Adding ones and ones, then tens

Adding ones and ones,
composing a ten explicitly

Other students may see that they can group 10 ones to make a new unit of ten (as they did when counting collections). They may show this awareness by making a new tower of 10 with connecting cubes or by marking or labeling a group of 10 in their base-ten drawings.

To deepen their understanding of place value and properties of operations, give students opportunities to compare and connect different methods, as well as to connect their method to representations that make sense to them (not limited to connecting cubes or base-ten drawings).

Students who rely on using known facts to add within 20 may apply the same method when adding within 100. They should not be required to use cubes or create drawings. However, encourage them to use representations, including equations, as they explain to others how their method works.

In this section, students apply what they learned about adding one- and two-digit numbers to add any numbers within 100—with and without composing a ten. They apply the associative and commutative properties as they count on, add tens and tens, and add ones and ones. Students see that no matter which order they use to combine parts of the addends, the sum remains the same.

They continue to use, interpret, and connect different methods and representations (including equations) that show a new unit of ten being composed from 10 ones.

Explain how Jada, Kiran, and Tyler each find the value of \(37 + 25\).

Jada’s way

\(30 + 20 = 50\)
\(7 + 5 = 12\)
\(50 + 12 = 62\)

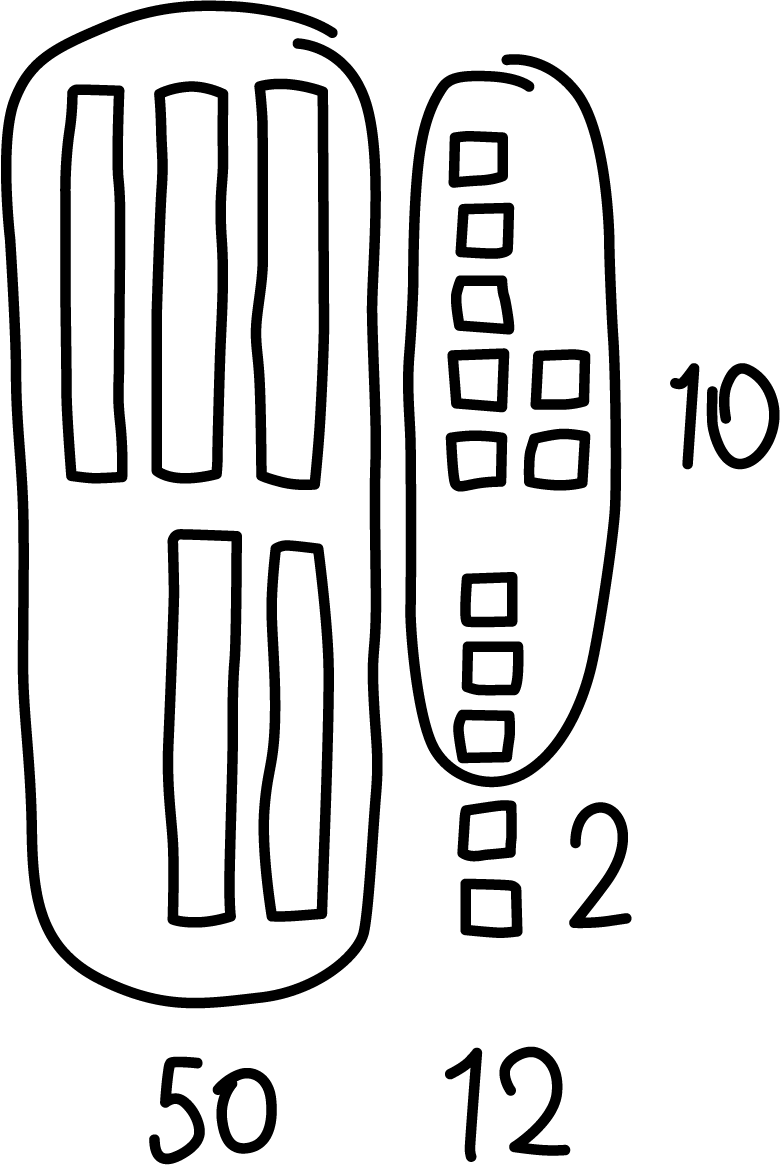
Kiran’s way

\(37 + 3 + 2 = 42\)
\(42 + 20 = 62\)

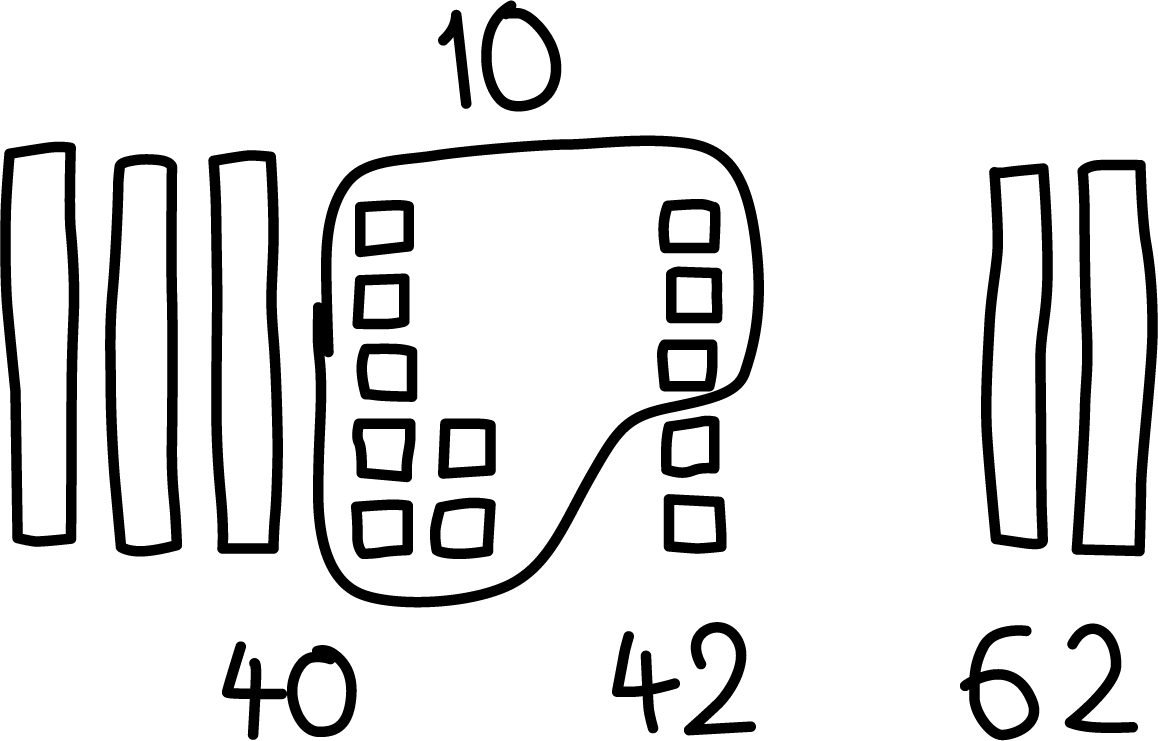
Tyler’s way

\(37 + 20 = 57\)
\(57 + 3 + 2 = 62\)

In this unit, students extend their knowledge of linear measurement while continuing to develop their understanding of operations, algebraic thinking, and place value.

In kindergarten, students identified attributes of objects that can be compared, such as length, weight, and capacity. In this unit, students compare the length of objects by lining them up at their endpoints, and explore ways to compare lengths of two objects that cannot be lined up.

From there, they transition to the idea of iterating length units, or using the same length unit allows us to measure the lengths of objects and to communicate measurements clearly.

Students begin by using the length of a connecting cube as a unit of measurement. Because connecting cubes snap together, students can focus on counting the length of the cubes without worrying about any gaps or overlaps in the units.

Later, students measure with length units that don’t connect together, such as paper clips and base-ten cubes (centimeter cubes), but do not refer to formal units of length. They develop precision as they make sure that there are no gaps or overlap in the units used to measure.

Some objects that students measure by iterating small units yield measurements of over 100 length units. Students consider how to count and represent these larger groups of objects—up to 120—with a written number. They use familiar representations (connecting cubes and base-ten drawings) to recognize 100 as 10 tens, but do not consider the unit of a hundred until grade 2.

Later in the unit, students solve problems in various contexts, including measurement. They revisit Compare, Difference Unknown story problems and learn to solve Compare, Bigger Unknown and Smaller Unknown problems about lengths. Next, students are introduced to a new problem type: Take From, Start Unknown. They practice solving all story problems types with unknowns in all positions.

In this section, students transition from direct comparison of lengths to indirect comparison. They reason about how they can compare the length of objects that cannot be easily lined up. 

Students begin this transition by ordering the length of three objects directly. Next, they compare two objects by using the length of a third object. 

For example, students may compare the pencil and the pen directly by lining them up and see that the pencil is shorter than the pen. Then, they may compare the pen and highlighter directly and see that the highlighter is longer than the pen.

Without comparing the pencil and highlighter directly, students could say that:

• The pencil is shorter than the highlighter because it is shorter than the pen.
• The highlighter is longer than the pencil because it is also longer than the pen.

At the end of the section, students practice using a third object as a tool to compare the length of objects that are very difficult to line up. For example, they use a string to compare the length of one side of a desk and the length of one of its legs.

The work here prepares students to iterate length units to measure objects in the next section.

In this section, students measure the length of objects by iterating length units. They learn the conventions of length measurement and represent their measurements with a number and the name of the length unit. They understand that the length measurement of an object is the number of same-size length units that span it without gaps or overlaps.

Students use manipulatives such as connecting cubes, paper clips, and base-ten cubes as length units. Other units of measurement that would yield a whole number of length units are also suggested.

It is important for students to measure lengths in whole units as they are developing the idea that the number of units for the same length would not change when measured by different people.

Students expand their counting and number-writing skills to 120 as they use base-ten cubes to measure lengths that are longer than 99 length units. Along the way, students consider groups of 10 and see that 10 tens is 100. A hundred is not discussed as a unit in grade 1, but the written notation is introduced so students can read and write the numbers 100–120.

In this section, students solve all types of story problems with unknowns in all positions. They interpret and write addition and subtraction equations that represent the problems.

Students begin by building and comparing concrete objects to solve Compare problems in the context of measurement. These problems involve Bigger or Smaller Unknown, a new problem type for students, and can be represented by diagrams such as shown here. 

Next, students solve Take From problems with unknowns in all positions with a focus on Start Unknown, another new problem type. These problems can be challenging because the action can be represented with subtraction, but solving the problem may involve adding. For example:

Regardless of the equation they write, students should focus on explaining how their equation matches the story problem.

In this unit, students focus on geometry and time. They expand their knowledge of two- and three-dimensional shapes, partition shapes into halves and fourths, and tell time to the hour and half of an hour. Center activities and warm-ups continue to enable students to solidify their work with adding and subtracting within 20 and adding within 100.

In kindergarten, students learned about flat and solid shapes. They named, described, built, and compared shapes. They learned the names of some flat shapes (triangle, circle, square, and rectangle) and some solid shapes (cube, sphere, cylinder, and cone).

Here, students extend those experiences as they work with shape cards, pattern blocks, geoblocks, and solid shapes. They develop increasingly precise vocabulary as they use defining attributes (“squares have four equal length sides”) rather than non-defining attributes (“the square is blue”) to describe why a specific shape belongs to a given category. Students should, however, focus on manipulating, comparing, and composing shapes and using their own language, rather than learning the formal definitions of shapes.

Draw 3 shapes that are not rectangles.

How do you know these are not rectangles?​​​​​​

Next, students transition to thinking about how to partition shapes into halves and fourths or quarters. These experiences allow them to learn the language of fractions. Students come to understand that as they continue to make more equal pieces, each piece gets smaller.

In the last section, students tell time to the hour and half hour. They learn about the hour and minute hands and what an analog clock looks like when the hour hand moves from one hour to the next. The experience of partitioning circles helps students make sense of time on the clock. Students see that half hours are when the minute hand has moved halfway around the clock, and the time can be written as “half past” or __ : 30.

In this section, students explore and reason about attributes of two- and three-dimensional shapes. They begin by sorting and describing shapes in ways that make sense to them. They name shapes (cone, sphere, cylinder, cube, square, rectangle, triangle, rhombus and hexagon), but do not need to hear or produce formal definitions of the shape. 

Students identify the defining attributes (number of straight sides and corners) of triangles, rectangles, and squares, and distinguish them from non-defining attributes (color, orientation, size). They describe why a shape belongs in a certain category using their own language. For example, “These are all triangles because they have three straight sides and three corners. This is not a triangle because the sides don’t touch.”

These are triangles.

These are not triangles.

Students learn that a square is a special rectangle, because it has all of the defining attributes of a rectangle (4 sides, 4 square corners) and also has the defining attribute of a square (4 equal length sides).

Students then compose shapes from smaller shapes to deepen their understanding of two- and three-dimensional shapes. The spatial reasoning here builds a foundation for understanding future mathematical concepts such as symmetry, congruence, fraction, area, and volume.

Geoblocks are used throughout the section. Standard geoblock sets do not include cylinders, spheres, and cones. When these shapes are required, “solid shapes” are indicated as required materials. If solid shapes are not available, students can work with everyday items that represent each shape.

In this section, students explore the idea of halves and fourths as equal pieces of a whole.

Students learn that when decomposing a shape into two equal pieces, each piece is “a half of” the shape, and the pieces are called halves. When a shape is decomposed into four equal pieces, each piece is “a fourth of” the shape, and the pieces are called fourths or quarters.

​​​​​

To create two and four equal pieces, students fold paper shapes and then draw lines to split the shapes. They consider the size of a fourth and a half in relation to the same whole, and notice that as the number of pieces increases, each piece gets smaller.

Split each shape into fourths.

Split each shape into halves.

In this section, students learn to tell time in hours and half hours on both analog and digital clocks by interpreting the position of the hands on the former and the digits of the latter. They connect the language of “o’clock” and “half past” to the times shown on analog and digital clocks.

Students begin by interpreting clock faces that only show an hour hand. This is to draw their attention to the fact that the hour hand will point directly to a number at the hour and halfway in between two numbers at the half hour. Given their understanding of halves of shapes, students see that when the minute hand starts at the 12 and rotates to point at the 6, it has moved halfway around the clock.

To build students’ concept of time, consider preparing an alarm that goes off each half-hour to draw attention to time in hours and half hours. When the alarm goes off, students can look at the clock, draw the hands on a blank clock, and record the time using numbers.

Fill in the clocks to show what time each activity starts.

Arrival

Reading

Although the lessons in this section focus on 12-hour clocks, some students who are familiar with 24-hour clocks should be invited to share what they know.

In this unit, students revisit major work and fluency goals of the grade, applying their learning from the year. 

In Section A, students add and subtract within 20, concurrently working toward the goal of adding and subtracting fluently within 10. In Section B, they practice solving story problems of familiar types (those introduced in earlier units). In Section C, students count and represent numbers within 120.

Each of these topics is critical for students’ readiness for the work in grade 2, in which students will expand their understanding of place value and add and subtract within 100.

What number is shown?
Record an estimate that is too low, too high, and about right.

The sections in this unit are standalone sections, not required to be completed in order. The goal is to offer ample opportunities for students to integrate the knowledge they have gained and to practice skills related to the expected fluencies of the grade.

In this section, students practice adding and subtracting within 20. They also reflect on their fluency with addition and subtraction within 10—by completing an inventory of the sums and differences they do and do not yet know fluently. Students continue to work toward fluency with these expressions and to share the methods they find effective for finding the value of the expressions.

The relationship between addition and subtraction continues to be highlighted here. Doing so reinforces the idea that knowing an addition fact can help us know the related subtraction facts. Students also recognize that they can use known sums and differences within 10 to find the value of sums and differences within 20.

Color the differences whose value you know from memory.

\(17 - 9 = \boxed{\phantom{8}}\)
\(9 + \boxed{\phantom{8}} = 17\)
\(9 + 1 + 7 = 17\)

\(9 + \boxed{8} = 17\), so \(17 - 9 = \boxed{8}\)

In this section, students revisit some types of story problems that were introduced in earlier units and should be mastered by the end of grade 1. These problem types include:

• Add to and Take From, Change Unknown
• Put Together and Take Apart, Addend Unknown
• Compare, Difference Unknown 

Clare saw 8 sea turtles swimming together in the tank.
Some more turtles joined them.
Now there are 15 turtles in the tank.
How many turtles joined the group?

Students solve problems in any way that makes sense to them, including creating discrete drawings for each story. Throughout the section, look for ways to connect the methods and representations they use. Doing so helps to deepen students’ understanding of the structure of the problem types and helps them progress toward using representations that are more abstract (such as equations). 

The activity and lesson syntheses in the section highlight the relationship between addition and subtraction and the idea of making a 10 to solve problems.