Lesson 6

A Proof of the Pythagorean Theorem

View Student Lesson

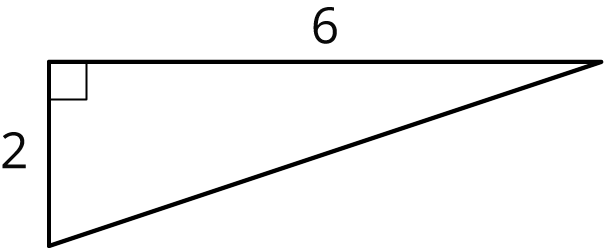
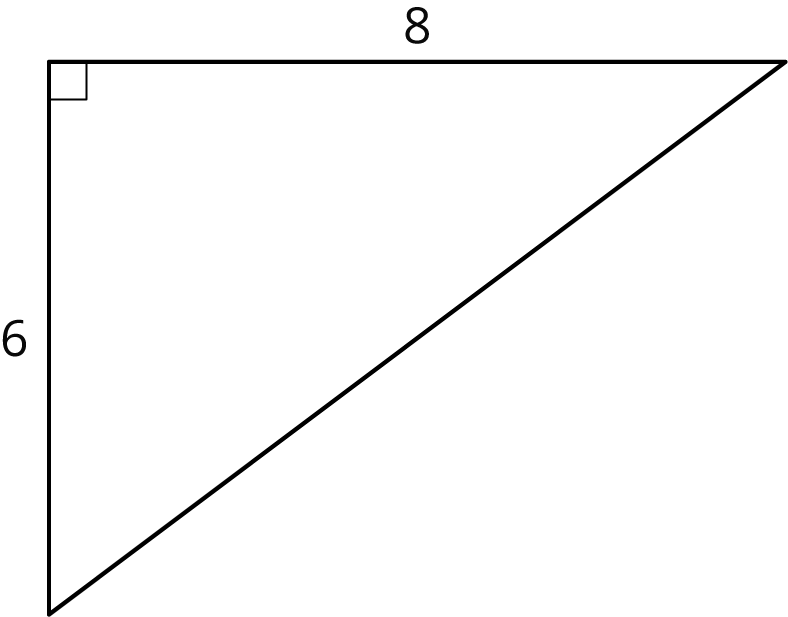
Problem 1

  1. Find the lengths of the unlabeled sides.
    A right triangle with a horizontal side on the top and a vertical side on the left. The top side is labeled 6 and the side on the left is labeled 2.
    A right triangle with a horizontal side on top and a vertical side on the left. The top side is labeled 8 and the left side is labeled 6.
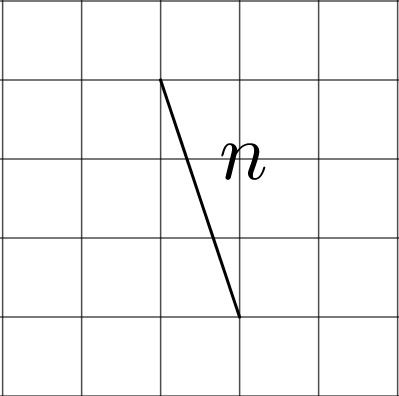
  2. One segment is \(n\) units long and the other is \(p\) units long. Find the value of \(n\) and \(p\). (Each small grid square is 1 square unit.)
    A line segment labeled “n” on a square grid.

    A line segment labeled “p” on a square grid.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

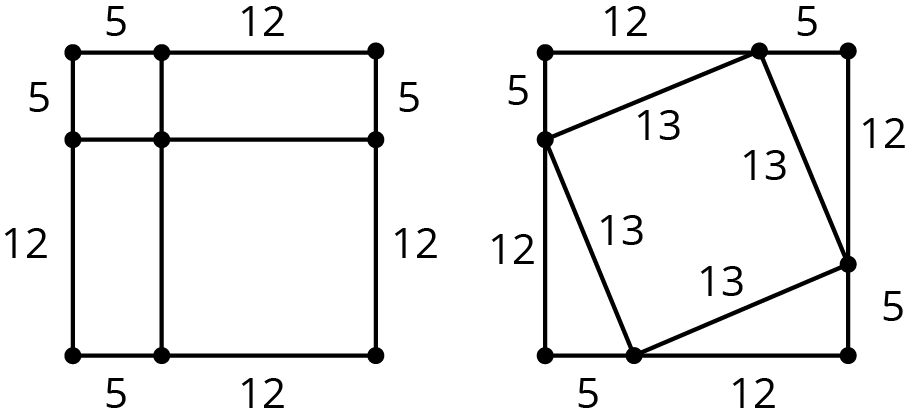
Use the areas of the two identical squares to explain why \(5^2+12^2=13^2\) without doing any calculations.

2 decomposed squares.

 

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Find the exact value of each variable that represents a side length in a right triangle.

5 right triangles. 

 

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Write each expression as a single power of 10.

  1. \(10^5 \boldcdot 10^0\)
  2. \(\frac{10^9}{10^0}\)

Solution

For access, consult one of our IM Certified Partners.

(From Unit 7, Lesson 4.)

Problem 5

Here is a scatter plot of weight vs. age for different Dobermans. The model, represented by \(y = 2.45x + 1.22\), is graphed with the scatter plot. Here, \(x\) represents age in weeks, and \(y\) represents weight in pounds.

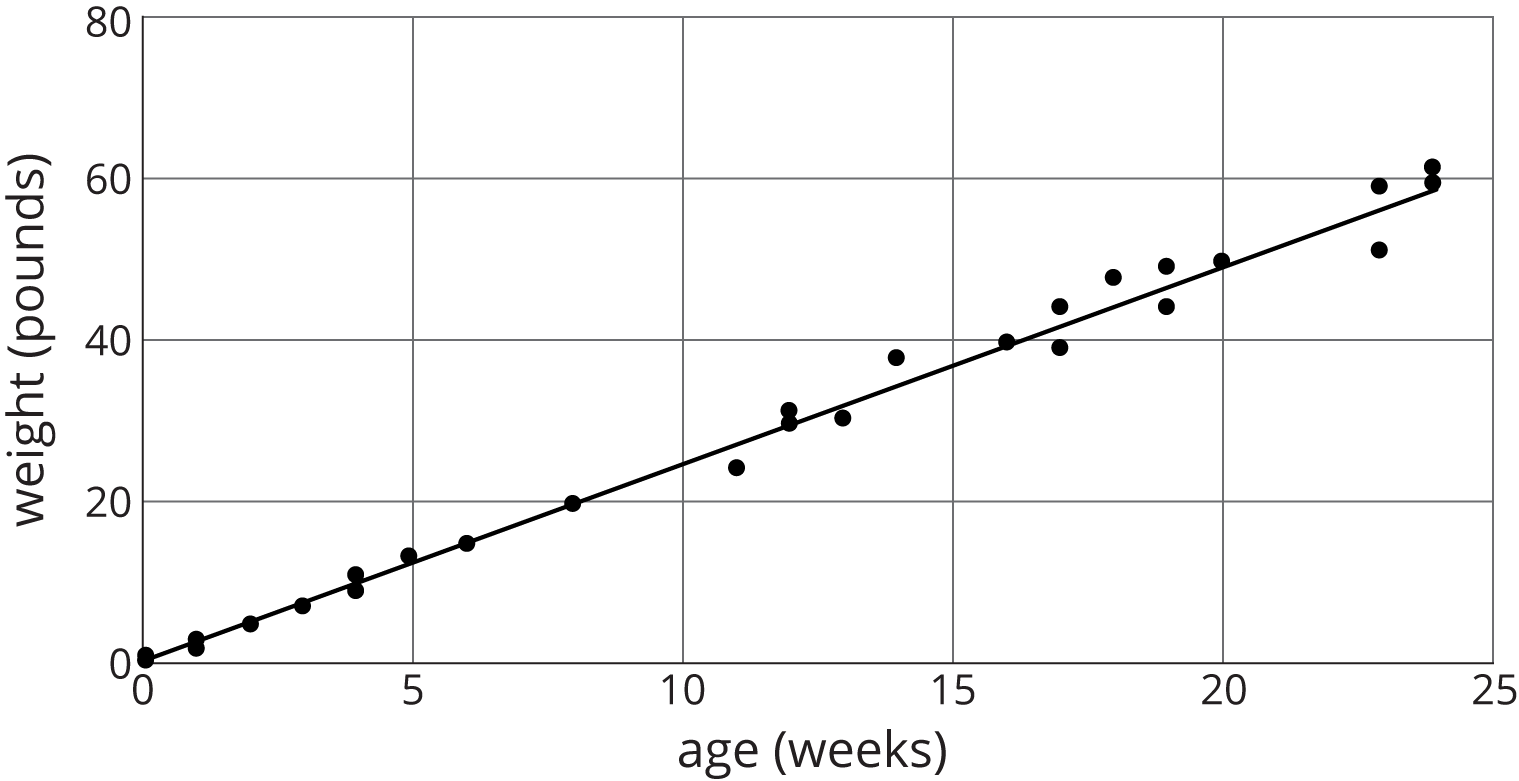
Scatter plot with line of best fit. Horizontal axis, age in weeks, scale 0 to 25, by 5’s. Vertical axis, weight in pounds, scale 0 to 80, by 20’s. 
  1. What does the slope mean in this situation?
  2. Based on this model, how heavy would you expect a newborn Doberman to be?

Solution

For access, consult one of our IM Certified Partners.

(From Unit 5, Lesson 21.)