Lesson 3
Rational and Irrational Numbers
3.1: Algebra Talk: Positive Solutions (5 minutes)
Warm-up
The purpose of this warm-up is for students to review multiplication of fractions in preparation for the main problem of this lesson: estimating solutions to the equation \(x^2=2\). For example, \(\frac32 \boldcdot \frac32 = \frac94\), which is a value close to 2 so \(\frac32\) is a value close to \(\sqrt{2}\). For this activity it is best if students work with fractions and do not convert any numbers to their decimal forms. Answers expressed in decimal form aren’t wrong, but if students work with decimal forms, they will miss out on the purpose of this warm-up.
While four problems are given, it may not be possible to share every strategy. Consider gathering only two or three different strategies per problem.
Launch
Ask students, “Could 8 be a solution to \(x^2 = 49\)? Why or why not?”
Display one problem at a time. Give students 30 seconds of quiet think time for each problem, and ask them to give a signal when they have an answer and a strategy. Keep all previous problems displayed throughout the talk. Follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Find a positive solution to each equation:
\(x^2=36\)
\(x^2=\frac94\)
\(x^2=\frac14\)
\(x^2=\frac{49}{25}\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their responses for all to see. At the end of the discussion, ask students to explain what they know about multiplication of fractions that helped them find the value of \(x^2\) in each problem.
To involve more students in the conversation, consider asking:
-
“Did anyone have the same strategy but would explain it differently?”
-
“Did anyone solve for the value of \(x\) in a different way?”
-
“Does anyone want to add on to _____’s strategy?”
- “Do you agree or disagree? Why?”
Design Principle(s): Optimize output (for explanation)
3.2: Three Squares (10 minutes)
Activity
This activity is the first of three activities in which students investigate the value of \(\sqrt2\). In this activity, students draw three squares on small grids, building on their earlier work. Two of the three possible squares have easily countable side lengths since they line up along the grid lines. The third likely possibility, that of a tilted square with vertices at the midpoint of each side of the grid, has sides equal to the length of a diagonal of a 1 unit square.
Monitor for students who:
- compare lengths directly by either creating a grid ruler or by tracing a segment with tracing paper and bringing it side by side with another segment. Most likely these students will say that the side length of the tilted square is around 1.5 units (or possibly, a little bit less than 1.5 units).
- who recall the square root notation from the previous lesson and expressed the side length of the tilted square as \(\sqrt{2}\). Since the area of the tilted square is 2 square units, we can express its side length as \(\sqrt{2}\) units.
If we use tracing paper or create a ruler scaled the same way as the grid, it can be seen that \(\sqrt{2}\) is a bit less than 1.5. In the next activity, students will look for a more precise value of \(\sqrt{2}\).
Launch
Provide access to tracing paper. Display the image from the task statement for all to see, and note that there are 9 vertices in each 2-by-2 grid. Students are asked in this activity to draw “squares of different sizes with vertices aligned to the vertices of the grid,” so make sure they can interpret this correctly. It may be helpful to draw a few non-examples.
This has vertices aligned to the grid, but is not a square:

This looks like a square, but doesn’t have vertices aligned to the grid:

Supports accessibility for: Conceptual processing
Student Facing

-
Draw 3 squares of different sizes with vertices aligned to the vertices of the grid.
-
For each square:
-
Label the area.
-
Label the side length.
-
Write an equation that shows the relationship between the side length and the area.
-
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some will say the side length of the tilted square is 1 unit, because a common misconception is that the diagonal of a square has a length of 1 unit. Ask students if the square has the same area as a grid square.
Activity Synthesis
First, select students who tried to compare the lengths directly by either creating a grid ruler or by tracing a segment with tracing paper and bringing it side by side with another segment during the discussion. Highlight the use of rotating figures to align sides in order to compare their lengths. Most likely these students will say that the side length of the tilted square is around 1.5 units (or possibly, a little bit less than 1.5 units).
Then, select students who recall the square root notation from the previous lesson and expressed the side length of the tilted square as \(\sqrt{2}\). Since the area of the tilted square is 2 square units, its side length can be expressed as \(\sqrt{2}\) units. This activity shows that \(\sqrt{2}\) is around 1.5. In the next activity, students will look for a more precise value of \(\sqrt{2}\).
Design Principle(s): Support sense-making
3.3: Looking for a Solution (10 minutes)
Activity
This activity is the second of three activities in which students investigate the value of \(\sqrt2\). As a result of the previous activity, students should believe that \(\sqrt2\) is about 1.5, maybe a little bit less.
Students should also understand that \(\sqrt2\) is a number that we can multiply by itself and get a 2, so this is true:
\(\displaystyle \sqrt2 \boldcdot \sqrt2 = 2\)
The goal of this activity is to achieve a more precise value of \(\sqrt2\) than “about 1.5, maybe a little less.” In other words, an exact solution to \(x^2=2\) is required. In this activity, students will consider whether certain candidates are solutions to this equation.
In the whole-class discussion that follows, rational number is defined.
Launch
Remind students that 1.5 is equivalent to \(\frac32\). Students in groups of 2. Give 2–3 minutes quiet work time followed by partner then a whole-class discussion.
Supports accessibility for: Language; Social-emotional skills
Design Principles(s): Optimize output (for explanation); Maximize meta-awareness
Student Facing
Are any of these numbers a solution to the equation \(x^2=2\)? Explain your reasoning.
-
1
-
\(\frac12\)
-
\(\frac32\)
-
\(\frac75\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select students to share their reasoning for why each number is not a solution to \(x^2=2\). If students do not point it out, make sure that they notice that \(\frac32\) is not a terrible approximation for \(\sqrt2\), since \(\left( \frac32 \right)^2 = \frac94\), and \(\frac94\) is only a bit larger than 2. \(\frac75\) is an even better approximation for \(\sqrt2\), since \(\left( \frac75 \right)^2 = \frac{49}{25}\), which is just a little bit smaller than \(\frac{50}{25}\) (which equals 2). If you have posted a list of perfect squares in the room for reference, refer to this list during the discussion, because that list will come in handy when students work on the next activity.
This is where we want to define rational number. A rational number is a fraction or its opposite. Remember that a fraction is a number on the number line that you get by dividing the unit interval into \(b\) equal parts and finding the point that is \(a\) of them from 0. We can always write a fraction in the form \(\frac{a}{b}\) where \(a\) and \(b\) are whole numbers (and \(b\) is not 0), but there are other ways to write them. For example, 0.4 is a fraction because it is the point on the number line you get by dividing the unit interval into 10 equal parts and finding the point that is 4 away from 0. (You get the same point if you divide the unit interval into 5 equal parts and find the point that is 2 away from 0.) When we first learned about fractions, we didn’t know about negative numbers. Rational numbers are fractions, but they can be positive or negative. So, \(\text -\frac25\) is also a rational number.

Here are some examples of rational numbers: \(\displaystyle \frac{7}{4}, 0, \frac63, 0.2, \text-\frac{1}{3}, \text-5, \sqrt{9}, \text-\frac{\sqrt{16}}{\sqrt{100}}\) Can you see why they are each “a fraction or its opposite?”
Because fractions and ratios are closely related ideas, fractions and their opposites are called RATIOnal numbers.
3.4: Looking for $\sqrt2$ (10 minutes)
Activity
This activity is the third of three activities in which students investigate the value of \(\sqrt{2}\). In the previous activity, students saw that \(\frac75\) is a pretty good approximation for \(\sqrt2\). \(\sqrt2\) is a number when multiplied by itself equals 2, and \(\frac75\) multiplied by itself is pretty close to 2, it’s \(\frac{49}{25}\). In the discussion of the previous activity, students also learned (or were reminded of) the definition of rational number: a fraction or its opposite.
In this activity, students have a chance to look for some more rational numbers that are close to \(\sqrt2\). The idea is that they will look, for a while, for a fraction that can be multiplied by itself where the product is exactly 2. Of course, they won’t find one, because there is no such number. In the whole-class discussion that follows, irrational number is defined.
Launch
For this activity, it is best if students do not have access to a calculator with a square root button. A calculator that shows 9 decimal places will tell you that \(\sqrt2=1.414213562\) (which is not true) and that \(1.414213562^2=2\) (which is also not true). (To convince students that the calculator is lying to them, you have to make them multiply 1.414213562 by itself by hand, so better to sidestep the issue for now.) It would be handy for students to refer to a list of perfect squares while working on this activity, so consider posting such a list and drawing students’ attention to it.
Before they get started, remind students that a rational number is a fraction or its opposite, for example, \(\frac98\). Let them know that terminating decimals are also rational, for example, \(0.7 = \frac{7}{10}\).
As students work, it is possible they will focus on numbers in decimal form when searching for a rational number close to \(\sqrt2\). If you see this, encourage students to remember their work in the previous activity and the example of \(\frac75\), whose square, \(\frac{49}{25}\), was very close to 2. Are there any other values like \(\frac75\) that might be even closer to \(\sqrt2\)?
Since students could search indefinitely for a solution to the last problem with no success, ask students to stop their work in order to leave 3–4 minutes for a whole-class discussion.
Supports accessibility for: Conceptual processing; Memory
Design Principle(s): Support sense-making; Maximize meta-awareness
Student Facing
A rational number is a fraction or its opposite (or any number equivalent to a fraction or its opposite).
- Find some more rational numbers that are close to \(\sqrt2\).
- Can you find a rational number that is exactly \(\sqrt2\)?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
If you have an older calculator evaluate the expression\(\displaystyle \left(\frac{577}{408}\right)^2\)and it will tell you that the answer is 2, which might lead you to think that \(\sqrt{2}=\frac{577}{408}\).
- Explain why you might be suspicious of the calculator’s result.
-
Find an explanation for why \(408^2\boldcdot 2\) could not possibly equal \(577^2\). How does this show that \(\left(\frac{577}{408}\right)^2\) could not equal 2?
- Repeat these questions for\(\displaystyle \left(\frac{1414213562375}{10000000000000}\right)^2\neq 2,\)an equation that even many modern calculators and computers will get wrong.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ideally, students were given time to look for a rational number that is a solution to \(x^2=2\). Select students with particularly close values to share their number with the class and what strategy they used to find it. Applaud students for their perseverance, but confess that no such number exists because it is an irrational number.
Display a number line for all to see such as the one shown here. Tell students that an irrational number is a number that is not rational. That is, it is a number that is not a fraction or its opposite. \(\sqrt2\) is one example of an irrational number. It has a location on the number line, and its location can be narrowed down (it’s a tiny bit to the right of \(\frac{7}{5}\)), but \(\sqrt2\) cannot be found on a number line by subdividing the unit interval into \(b\) parts and taking \(a\) of them. We have to define \(\sqrt{2}\) in a different way, such as the side length of a square with area 2 square units.
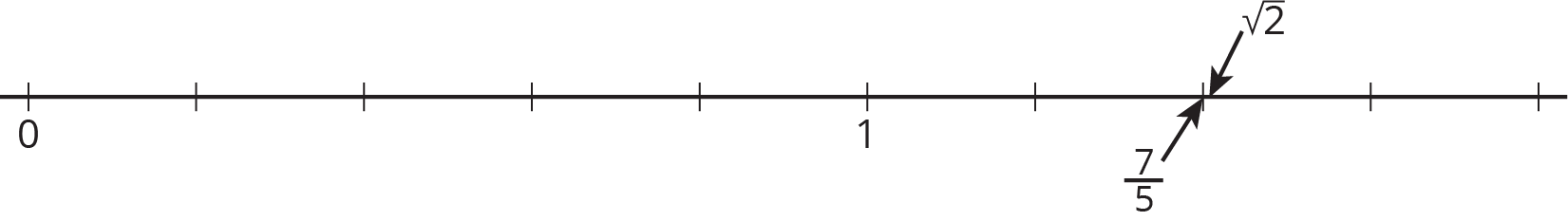
Just looking for rational solutions to \(x^2=2\) and not finding any is not a proof that \(\sqrt2\) is irrational. But for the purposes of this course, students are asked to take it as a fact that \(\sqrt2\) is irrational. In students’ future studies, they may have opportunities to understand or write a proof that \(\sqrt2\) is irrational.
While the activities focus specifically on \(\sqrt{2}\), there is nothing particularly special about this example. The square root of a whole number is either a whole number or irrational, so \(\sqrt{10}\), \(\sqrt{67}\), etc., are all irrational. Beyond grade level but worth having on hand for the sake of discussion is that rational multiples of irrational numbers are also irrational, so numbers like \(5\sqrt{7}\), \(\text -\sqrt{45}\), and \(\frac{\sqrt{5}}{3}\) are also irrational.
Lesson Synthesis
Lesson Synthesis
The purpose of this discussion is to explicitly point out that while we have collected some evidence that supports the claim that \(\sqrt{2}\) is irrational, we have not actually proved this claim. Here are some possible questions for discussion:
- “If I told you that there are no purple zebras, and you spent your whole life traveling the world and never saw a purple zebra, does it mean I was right?” (No, it is possible you just failed to find a purple zebra.)
- “So if we spent our whole lives testing different fractions and never quite got one whose square is 2, does that mean there are no such fractions?” (No, maybe you just haven’t found it yet.)
Tell students that we haven’t learned enough to prove for sure that \(\sqrt2\) is not equivalent to a fraction. For now, we just have to trust that there are numbers on the number line that are not equivalent to a fraction and that \(\sqrt2\) is one of them. However, it is possible to get very close estimates with fractions.
3.5: Cool-down - Types of Solutions (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
In an earlier activity, we learned that square root notation is used to write the length of a side of a square given its area. For example, a square whose area is 2 square units has a side length of \(\sqrt{2}\) units, which means that\(\displaystyle \sqrt{2} \boldcdot \sqrt{2} = 2.\)
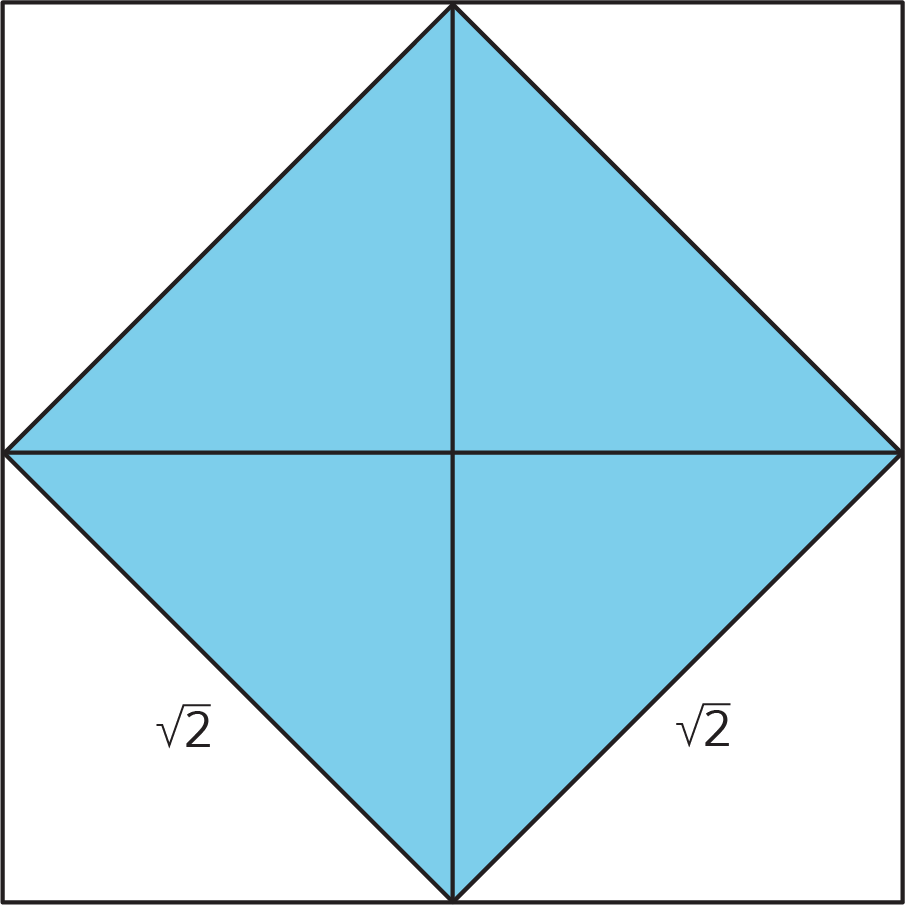
A square whose area is 25 square units has a side length of \(\sqrt{25}\) units, which means that \(\displaystyle \sqrt{25} \boldcdot \sqrt{25} = 25.\)Since \(5 \boldcdot 5 = 25\), we know that \(\displaystyle \sqrt{25}=5.\)
\(\sqrt{25}\) is an example of a rational number. A rational number is a fraction or its opposite. Remember that a fraction \(\frac{a}{b}\) is a point on the number line found by dividing the segment from 0 to 1 into \(b\) equal intervals and going \(a\) of those intervals to the right of 0. We can always write a fraction in the form \(\frac{a}{b}\) where \(a\) and \(b\) are whole numbers (and \(b\) is not 0), but there are other ways to write them. For example, we can write \(\sqrt{25} = \frac{5}{1}\). You first learned about fractions in earlier grades, and at that time, you probably didn't know about negative numbers. Rational numbers are fractions, but they can be positive or negative. So, -5 is also a rational number. Because fractions and ratios are closely related ideas, fractions and their opposites are called RATIOnal numbers.
Here are some examples of rational numbers: \(\displaystyle \frac{7}{4},\text{ } 0,\frac63, 0.2, \text-\frac{1}{3},\text-5, \sqrt{9},\text{ -}\frac{\sqrt{16}}{\sqrt{100}}\) Can you see why they are each examples of “a fraction or its opposite?”
An irrational number is a number that is not rational. That is, it is a number that is not a fraction or its opposite. \(\sqrt{2}\) is an example of an irrational number. It has a location on the number line, and its location can be approximated by rational numbers (it's a tiny bit to the right of \(\frac75\)), but \(\sqrt{2}\) can not be found on a number line by dividing the segment from 0 to 1 into \(b\) equal parts and going \(a\) of those parts away from 0 (if \(a\) and \(b\) are whole numbers).
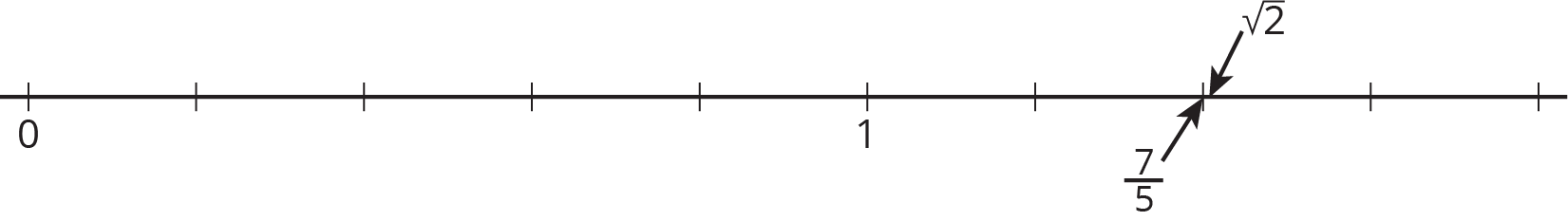
\(\frac{17}{12}\) is also close to \(\sqrt{2}\), because \(\left( \frac{17}{12} \right)^2=\frac{289}{144}\). \(\frac{289}{144}\) is very close to 2, since \(\frac{288}{144}=2\). But we could keep looking forever for solutions to \(x^2=2\) that are rational numbers, and we would not find any. \(\sqrt2\) is not a rational number! It is irrational.
In your future studies, you may have opportunities to understand or write a proof that \(\sqrt2\) is irrational, but for now, we just take it as a fact that \(\sqrt2\) is irrational. Similarly, the square root of any whole number is either a whole number (\(\sqrt{36}=6\), \(\sqrt{64}=8\), etc.) or irrational (\(\sqrt{17}\), \(\sqrt{65}\), etc.). Here are some other examples of irrational numbers:\(\displaystyle \sqrt{10}, \text{ -}\sqrt3, \text{ }\frac{\sqrt5}{2},\text{ } \pi\)