Lesson 5

Finding Side Lengths of Triangles

This is the first of three lessons in which students investigate relationships between the side lengths of right and non-right triangles leading to the Pythagorean Theorem.

In the warm-up for this lesson, students notice and wonder about 4 triangles. While there is a lot to notice, one important aspect is whether the triangle is a right triangle or not. This primes them to notice patterns of right and non-right triangles in the other activities in the lesson. In the next two activities, students systematically look at the side lengths of right and non-right triangles for patterns (MP8). By the end of this lesson, they see that for right triangles with legs $a$ and $b$ and hypotenuse $c$, the side lengths are related by $a^2+b^2=c^2$. In the next lesson they will prove the Pythagorean Theorem.

Teacher Notes for IM 6–8 Math Accelerated

Due to the arrangement of lessons in IM 6–8 Math Accelerated, this is the first of 2 lessons in which students investigate relationships between the side lengths of right and non-right triangles leading to the Pythagorean Theorem, not the first of 3 as stated in the narrative.

Comprehend the term “Pythagorean Theorem” (in written and spoken language) as the equation $a^2+b^2=c^2$ where $a$ and $b$ are the lengths of the legs and $c$ is the length of the hypotenuse of a right triangle.
Describe (orally) patterns in the relationships between the side lengths of triangles.
Determine the exact side lengths of a triangle in a coordinate grid and express them (in writing) using square root notation.

Let’s find triangle side lengths.

I can explain what the Pythagorean Theorem says.

Building On

Addressing

8.G.B

Building Towards

Pythagorean Theorem

The Pythagorean Theorem describes the relationship between the side lengths of right triangles.

The diagram shows a right triangle with squares built on each side. If we add the areas of the two small squares, we get the area of the larger square.

The square of the hypotenuse is equal to the sum of the squares of the legs. This is written as $a^2+b^2=c^2$.
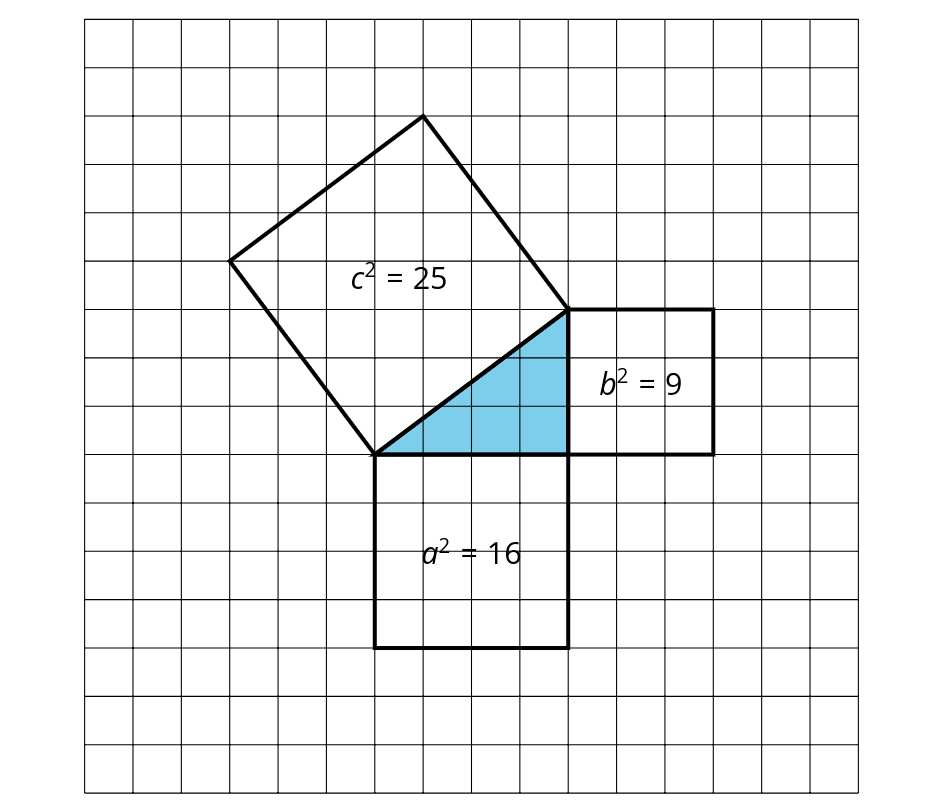
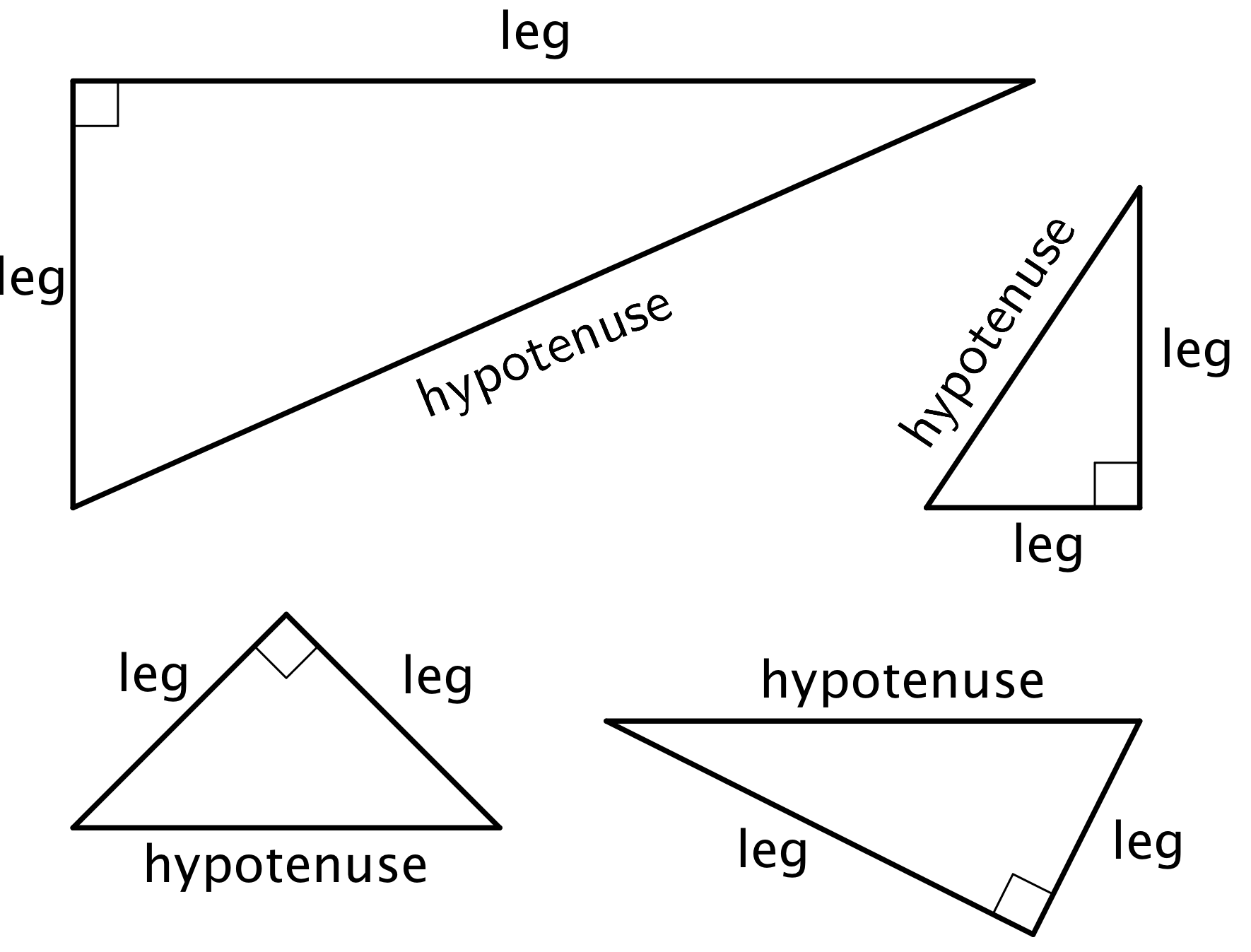
hypotenuse

The hypotenuse is the side of a right triangle that is opposite the right angle. It is the longest side of a right triangle.

Here are some right triangles. Each hypotenuse is labeled.
legs

The legs of a right triangle are the sides that make the right angle.

Here are some right triangles. Each leg is labeled.