Lesson 12

Balanced Moves

View Student Lesson

Problem 1

In this hanger, the weight of the triangle is \(x\) and the weight of the square is \(y\).

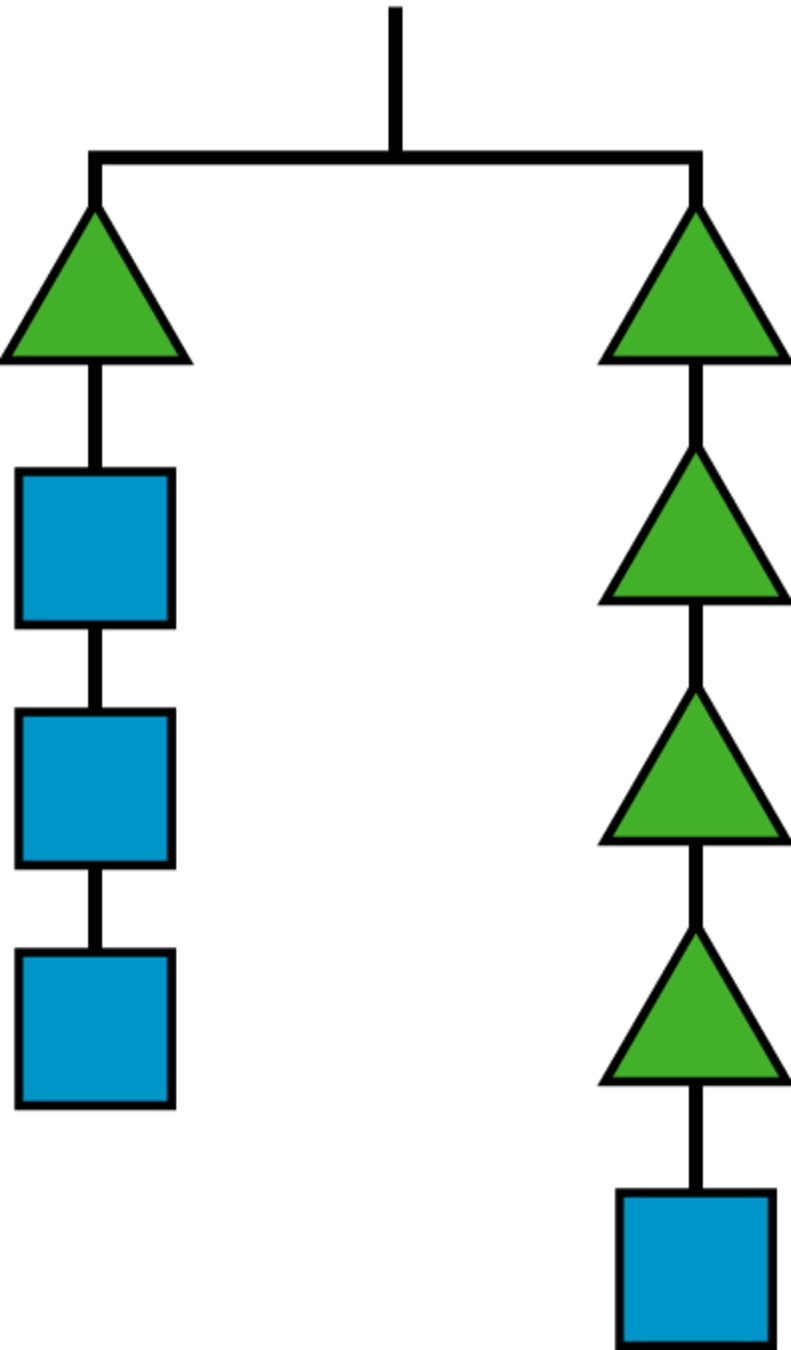
Balanced hanger. Left side, 1 triangle, 3 squares. Right side, 4 triangles, 1 square. 

  1. Write an equation using \(x\) and \(y\) to represent the hanger.

  2. If \(x\) is 6, what is \(y\)?

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Andre and Diego were each trying to solve \(2x+6=3x-8\). Describe the first step they each make to the equation.

  1. The result of Andre’s first step was \(\text-x+6=\text-8\).
     

     
  2. The result of Diego’s first step was \(6=x-8\).
     

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Match each set of equations with the move that turned the first equation into the second.

A:

\(6x + 9 = 4x -3\)
\(2x + 9 = \text-3\)

B:

\(\text-4(5x-7) = \text-18\)
\(5x-7 = 4.5\)

C:

\(8-10x = 7+5x\)
\(4-10x = 3+ 5x\)

D:

\(\frac {\text{-}5x}{4} = 4\)
\(5x=\text-16\)

E:

\(12x+4 = 20x+24\)
\(3x+1=5x+6\)

1:

Multiply both sides by \(\frac {\text{-}1}{4}\)

2:

Multiply both sides by \(\text-4\)

3:

Multiply both sides by \(\frac14\)

4:

Add \(\text-4x\) to both sides

5:

Add \(\text-4\) to both sides

Solution

For access, consult one of our IM Certified Partners.

Problem 4

What is the weight of a square if a triangle weighs 4 grams?

Explain your reasoning.

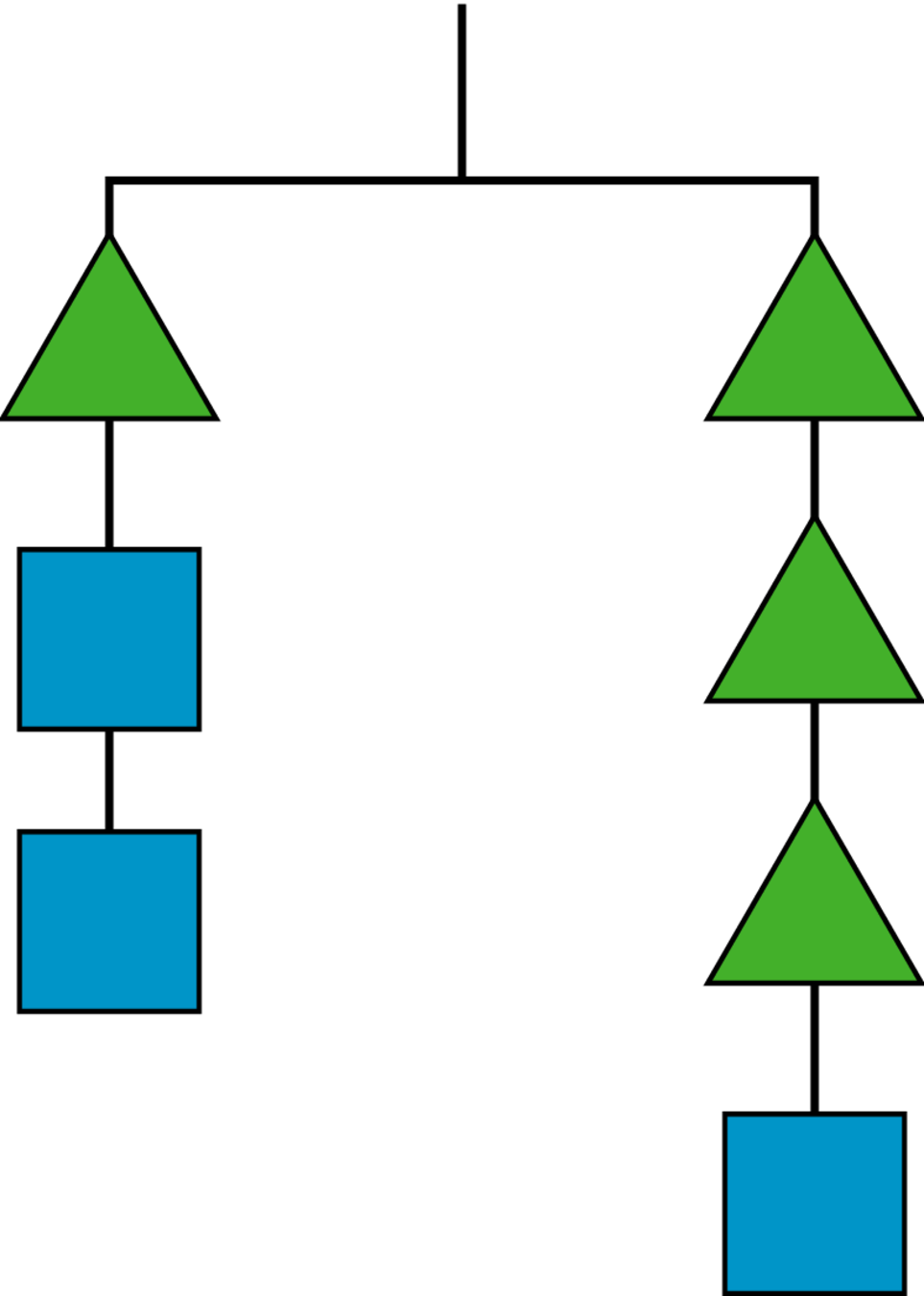
Balanced hanger. Left side, 1 triangle, 2 squares. Right side, 3 triangles, 1 square. 

Solution

For access, consult one of our IM Certified Partners.

Problem 5

Here is a balanced hanger diagram.

Each triangle weighs 2.5 pounds, each circle weighs 3 pounds, and \(x\) represents the weight of each square. Select all equations that represent the hanger.

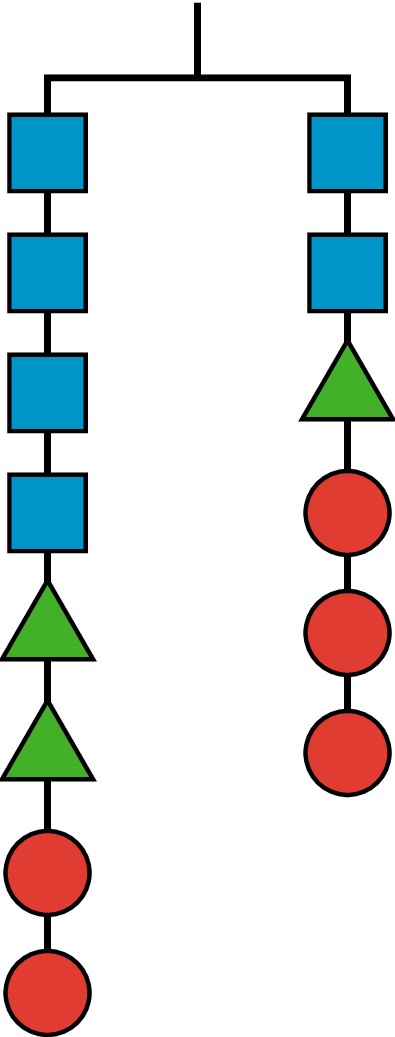
A balanced hanger. Left side, 4 squares, 2 triangles, 2 circles. Right side, 2 squares, 1 triangle, 3 circles.
A:

\(x+x+x+x+11=x+11.5\)

B:

\(2x=0.5\)

C:

\(4x+5+6=2x+2.5+6\)

D:

\(2x+2.5=3\)

E:

\(4x+2.5+2.5+3+3=2x+2.5+3+3+3\)

Solution

For access, consult one of our IM Certified Partners.