Lesson 8
Percentage Situations
8.1: Tax, Tip, and Discount (5 minutes)
Warm-up
In this warm-up, students are reminded of the tape diagram method for understanding parts of a whole. The tape diagrams are used in the context of tips, taxes, and discounts.
Launch
Students in groups of 2. Allow students 2 minutes quiet work time followed by partner then whole-class discussion.
Student Facing
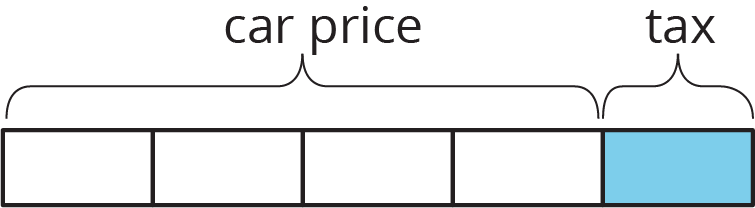
What percentage of the car price is the tax?
What percentage of the food cost is the tip?

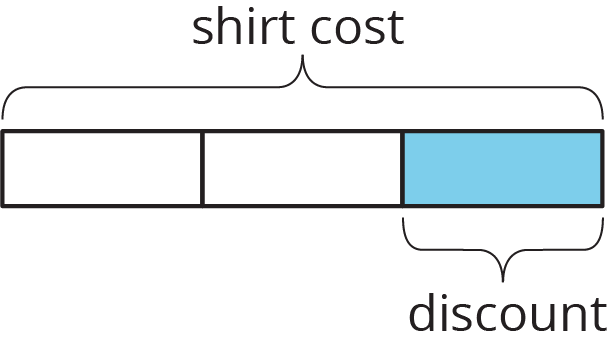
What percentage of the shirt cost is the discount?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of the discussion is for students to recognize that a tape diagram can be useful for working with percentages as part of a whole.
Consider asking these discussion questions:
- "The tax on the car is what fraction of the car price before tax was added on?" (One fourth)
- "With the tip added on, how is the length of the entire bar related to the length of the bar that just represents the food cost?" (It is 1.2 times as long.)
- "How does the value \(\frac{2}{3}\) relate to the last tape diagram?" (It represents the fraction of the original cost of the shirt that is the price of the shirt after the discount.)
8.2: A Car Dealership (10 minutes)
Activity
The purpose of this activity is to introduce students to a context involving markups and markdowns or discounts, and to connect this to the work on percent increase and percent decrease they did earlier. The first question helps set the stage for students to see the connection to markups and percent increase. Look for students who solve the second question by finding 90% of the retail price, and highlight this approach in the discussion.
Launch
Tell students that a mark-up is a percentage that businesses often add to the price of an item they sell, and a mark-down is a percentage they take off of a given price. If helpful, review the meaning of wholesale (the price the dealership pays for the car) and retail price (the price the dealership charges to sell the car). Sometimes people call mark-downs discounts.
Provide access to calculators. Students in groups of 2. Give students 5 minutes of quiet work time, followed by partner then whole-class discussion.
Design Principle(s): Support sense-making
Student Facing
A car dealership pays a wholesale price of $12,000 to purchase a vehicle.
-
The car dealership wants to make a 32% profit.
- By how much will they mark up the price of the vehicle?
- After the markup, what is the retail price of the vehicle?

- During a special sales event, the dealership offers a 10% discount off of the retail price. After the discount, how much will a customer pay for this vehicle?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
This car dealership pays the salesperson a bonus for selling the car equal to 6.5% of the sale price. How much commission did the salesperson lose when they decided to offer a 10% discount on the price of the car?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
It is important throughout that students attend to the meanings of particular words and remain clear on the meaning of the different values they find. For example, "wholesale price," "retail price," and "sale price" all refer to specific dollar amounts. Help students organize their work by labeling the different quantities they find or creating a graphic organizer.
Activity Synthesis
For the first question, help students connect markups to percent increase.
Select students to share solutions to the second question. Highlight finding 90% of the retail price, and reinforce that a 10% discount is a 10% decrease.
Ask them to describe how they would find (but not actually find) . . .
- "The retail price after a 12% markup?" (Multiply the retail price by 0.12, then add that answer to the retail price. Alternatively, multiply the retail price by 1.12.)
- "The price after a 24% discount?" (Multiply the retail price by 0.24, then subtract that answer from the retail price. Alternatively, multiply the retail price by 0.76.)
8.3: Commission at a Gym (10 minutes)
Activity
The purpose of this activity is to introduce students to the concept of a commission and to solve percentage problems in that context. Students continue to practice finding percentages of total prices in a new context of commission.
Monitor for students who use equations like \(c = r \boldcdot p\) where \(c\) is the commission, \(r\) represents the percentage of the total that goes to the employee, and \(p\) is the total price of the membership.
Launch
Tell students that a commission is the money a salesperson gets when they sell an item. It is usually used as an incentive for employees to try to sell more or higher priced items than they usually would. The commission is usually a percentage of the price of the item they sell.
Provide access to calculators. Students in groups of 2. Give students 2 minutes of quiet work time. Partner then whole-class discussion.
Student Facing
-
For each gym membership sold, the gym keeps $42 and the employee who sold it gets $8. What is the commission the employee earned as a percentage of the total cost of the gym membership?
-
If an employee sells a family pass for $135, what is the amount of the commission they get to keep?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may find the percentage of an incorrect quantity. Ask them to state, in words, what they are finding a percentage of.
Students may not understand the first question. Tell them that a membership is sold for a certain price and the money is split with \$42 going to the gym and \$8 going to the employee.
Activity Synthesis
Select students to share how they answered the questions.
During the discussion, draw attention to strategies for figuring out which operations to do with which numbers. In particular, strategies involving equations like \(c = r \boldcdot p\) where \(c\) is the commission, \(r\) represents the percentage of the total that goes to the employee, and \(p\) is the total price of the membership.
Design Principle(s): Maximize meta-awareness
8.4: Info Gap: Sporting Goods (20 minutes)
Activity
The purpose of this info gap activity is for students to identify the essential information needed to determine the total savings after various discounts are applied to different items.
The info gap structure requires students to make sense of problems by determining what information is necessary, and then to ask for information they need to solve it. This may take several rounds of discussion if their first requests do not yield the information they need (MP1). It also allows them to refine the language they use and ask increasingly more precise questions until they get the information they need (MP6).
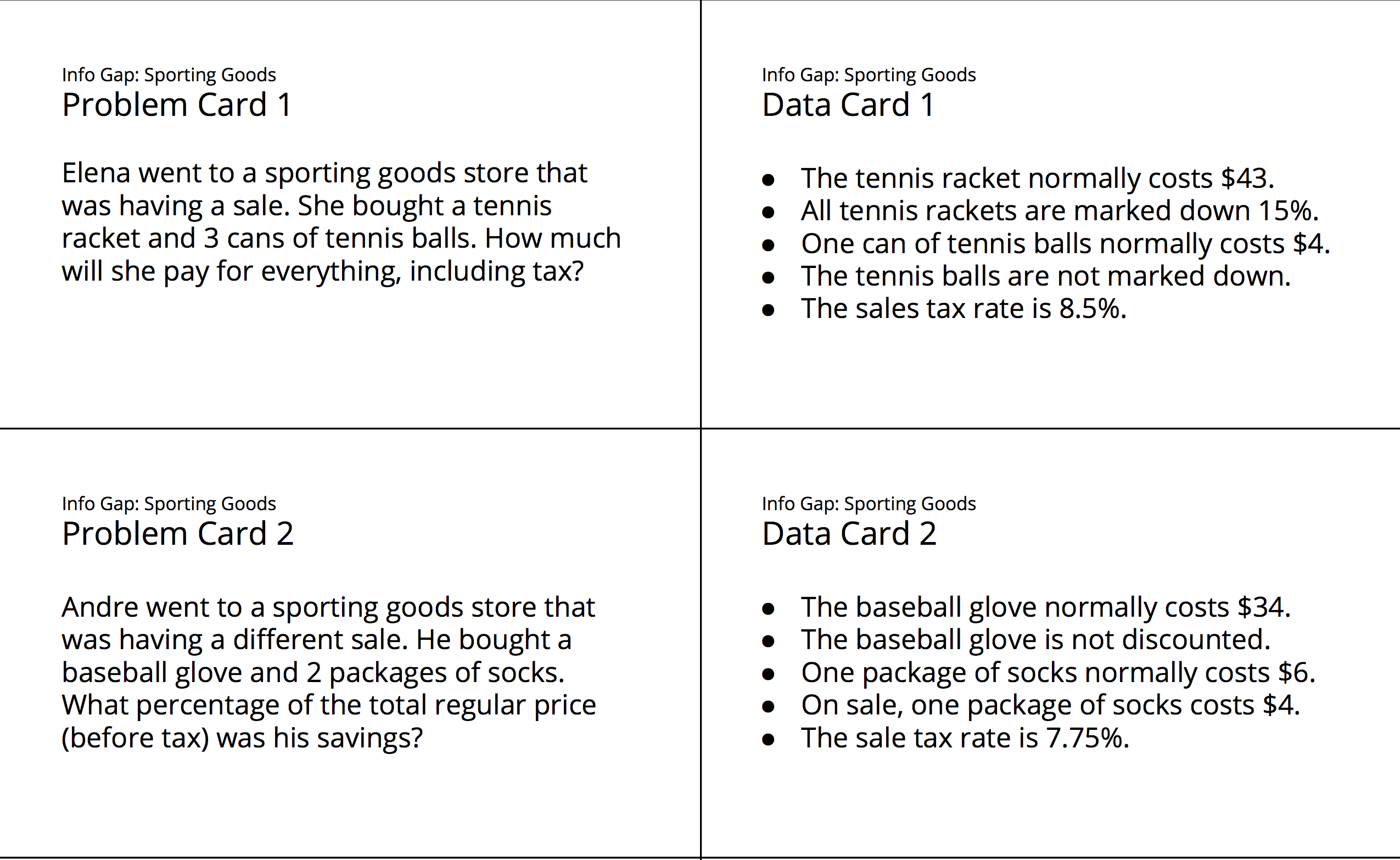
Here is the text of the cards for reference and planning:
Launch
Provide access to calculators. Tell students they will continue to work with percentages and their similarities to proportional relationships. Explain the Info Gap structure and consider demonstrating the protocol if students are unfamiliar with it. There are step-by-step instructions in the student task statement.
Arrange students in groups of 2. In each group, distribute a problem card to one student and a data card to the other student. After you review their work on the first problem, give them the cards for a second problem and instruct them to switch roles.
Supports accessibility for: Memory; Organization
Design Principle(s): Cultivate Conversation
Student Facing
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
-
Silently read your card and think about what information you need to be able to answer the question.
-
Ask your partner for the specific information that you need.
-
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
-
Share the problem card and solve the problem independently.
-
Read the data card and discuss your reasoning.
If your teacher gives you the data card:
-
Silently read your card.
-
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
-
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
-
Read the problem card and solve the problem independently.
-
Share the data card and discuss your reasoning.
Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students might fail to notice that Elena and Andre buy multiple cans of tennis balls and packages of socks, respectively. Ask students to figure out how much 2 packages of socks (or 3 cans of tennis balls) will cost.
If students automatically give the 15% discount on all of Elena's purchases, ask students which of Elena's items fall under the discount.
Students might apply the discount after the adding in the sales tax. Remind students that the discount gets applied to the subtotal before the tax is calculated.
Some students may include the sales tax when calculating the percentage of Andre's savings. Remind them that the problem specifies "before tax."
Activity Synthesis
The purpose of the discussion is for students to recognize what information may be needed to solve problems involving percentages for prices of items.
After students have completed their work, share the correct answers and ask students to discuss the different ways they solved this problem. Some guiding questions:
- "What information did you and your partner have to figure out?"
- "How did you determine the cost of Elena's tennis racket?" (Multiply the original cost by 0.85 or multiply by 0.15 and subtract from the original cost.)
- "How did you determine the total cost after tax for Elena's purchases?" (Multiply the total by 1.085 or multiply by 0.085 and add to the original cost.)
- "What different calculations did you have to make for Andre and Elena’s situations?"
- "Was there information given that you did not need to use?"
8.5: Card Sort: Percentage Situations (10 minutes)
Optional activity
This activity gives students an opportunity to practice various vocabulary terms that come along with percentages. Students are asked to sort scenarios to different descriptors using the images, sentences or questions found on the scenario cards. The questions found on the scenario cards are intended to help students figure out which descriptor the scenario card belongs under.
As students work on the task, identify students that are using the vocabulary: tip, tax, gratuity, commission, markup/down, and discount. These students should be asked to share during the discussion.
Launch
Arrange students in groups of 2. Distribute the sorting cards, and explain that students will sort 8 scenarios into one of 6 categories. Demonstrate how students can take turns placing a scenario under a category and productive ways to disagree. Here are some questions they might find useful:
- Which category would you sort this under?
- What do you think this word means?
- What words can we use as clues about where to sort this card?
Supports accessibility for: Conceptual processing; Organization
Design Principle(s): Optimize output (for explanation)
Student Facing
Your teacher will give you a set of cards. Take turns with your partner matching a situation with a descriptor. For each match, explain your reasoning to your partner. If you disagree, work to reach an agreement.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students should use the question at the bottom of the card to help them if they get stuck sorting the scenarios.
Activity Synthesis
Ask identified students to share which situations they sorted under each word. Ask them:
- "What made you decide to put these situations under this descriptor?"
- "Were there any situations that you were really unsure of? What made you decide on where to sort them?"
Consider asking some groups to order the situations from least to greatest in terms of the dollar amount of the increase of decrease and asking other groups to order them in terms of the percentage. Then, have them compare their results with a group that did the other ordering.
Answer students’ remaining questions about any of these contexts. Tell students there is a copy of this chart at the end of the lesson that they can use as a reference tool during future lessons. Allow them a space to take notes on their own to remember it or details from one of the activity examples.
| paid to: | how it works: | |
|---|---|---|
| sales tax | the government | added to the price of the item |
| gratuity (tip) | the server | added to the cost of the meal |
| interest | the lender (or account holder) | added to the balance of the loan, credit card, or bank account |
| markup | the seller | added to the price of an item so the seller can make a profit |
| markdown (discount) | the customer | subtracted from the price of an item to encourage the customer to buy it |
| commission | the salesperson | subtracted from the payment the store collects |
Lesson Synthesis
Lesson Synthesis
In this lesson, students examined additional situations in which percentages are often used and found the percentage increase or decrease. Consider asking these questions for students to discuss the main concepts from the lesson:
- “Give examples of situations in which you would encounter tax, tip, markup, markdown, or commission.” (Lots of possible answers.)
- “When an item is marked down 10%, why does it make sense to multiply the price by 0.9?” (Since there is 10% off the price, the new cost is 90% of the original.)
- “When an item is marked up 25%, why does it make sense to multiply the price by?” (Since the item now costs 100% plus an extra 25%, the new item costs 1.25 times the original.)
- “When the original price and discounted prices are known, how can we find the percent markdown?” (Find the difference and then find the percentage that difference is of the original price.)
- “When you know the original price of an item and the price you paid at a register, how can you find the tax rate?” (Find the difference and then find the percentage that difference is of the original price.)
8.6: Cool-down - Shoes on Sale (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
There are many everyday situations in which a percentage of an amount of money is added to or subtracted from that amount, in order to be paid to some other person or organization:
| goes to | how it works | |
|---|---|---|
| sales tax | the government | added to the price of the item |
| gratuity (tip) | the server | added to the cost of the meal |
| interest | the lender (or account holder) | added to the balance of the loan, credit card, or bank account |
| markup | the seller | added to the price of an item so the seller can make a profit |
| markdown (discount) | the customer | subtracted from the price of an item to encourage the customer to buy it |
| commission | the salesperson | subtracted from the payment that is collected |
For example, if a restaurant bill is $34 and the customer pays $40, they left 6 dollars as a tip for the server. That is 18% of $34, so they left an 18% tip. From the customer's perspective, we can think of this as an 18% increase of the restaurant bill. If we know the initial amount and the final amount, we can also find the percent increase or percent decrease. For example, a plant was 12 inches tall and grew to be 15 inches tall. What percent increase is this? Here are two ways to solve this problem:
The plant grew 3 inches, because \(15-12=3\). We can divide this growth by the original height, \(3\div 12 = 0.25\). So the height of the plant increased by 25%.
The plant's new height is 125% of the original height, because \(15 \div 12 = 1.25\). This means the height increased by 25%, because \(1.25 - 1 = 0.25\).
Here are two ways to solve the problem: A rope was 2.4 meters long. Someone cut it down to 1.9 meters. What percent decrease is this?
The rope is now \(2.4 - 1.9\), or 0.5 meters shorter. We can divide this decrease by the original length, \(0.5 \div 2.4 = 0.208\overline{3}\). So the length of the rope decreased by approximately 20.8%.
The rope's new length is about 79.2% of the original length, because \(1.9 \div 2.4 = 0.791\overline{6}\). The length decreased by approximately 20.8%, because \(1 - 0.792 = 0.208\).