Lesson 5
Percent Increase and Decrease with Equations
5.1: Number Talk: From 100 to 106 (5 minutes)
Warm-up
In this lesson, students will be finding percent increase and percent decrease by multiplying by an appropriate factor. For example, to find a 36% increase in a quantity, we can multiply that quantity by 1.36. This warm-up prompts them to think about the scale factor needed to multiply one number to get another.
Launch
Display one problem at a time. Give students 30 seconds of quiet think time per problem and ask them to give a signal when they have an answer and a strategy. Allow students to share their answers with a partner and note any discrepancies. Follow with a whole-class discussion.
Student Facing
How do you get from one number to the next using multiplication or division?
From 100 to 106
From 100 to 90
From 90 to 100
From 106 to 100
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their responses for all to see. To involve more students in the conversation, consider asking:
- “Who can restate \(\underline{\hspace{.5in}}\)’s reasoning in a different way?”
- “Did anyone have the same strategy but would explain it differently?”
- “Did anyone solve the problem in a different way?”
- “Does anyone want to add on to \(\underline{\hspace{.5in}}\)’s strategy?”
- “Do you agree or disagree? Why?”
Design Principle(s): Optimize output (for explanation)
5.2: Interest and Depreciation (10 minutes)
Activity
In this activity, students are calculating percent increase and decrease in the context of interest and depreciation. They may have encountered these contexts before this unit, but be sure that everyone understands the basic idea of interest and depreciation before students begin work.
Students have enough experience to solve these problems using various strategies and representations. Look for students writing different but correct expressions in terms of \(x\).
Launch
Remind students what interest is, give examples of when interest is applied (savings accounts, credit cards, etc.), and discuss depreciation value of an item.
Students in groups of 2. Give students 3–5 minutes of quiet work time, followed by partner then whole-class discussion.
Supports accessibility for: Conceptual processing; Visual-spatial processing
Student Facing
- Money in a particular savings account increases by about 6% after a year. How much money will be in the account after one year if the initial amount is $100? $50? $200? $125? \(x\) dollars? If you get stuck, consider using diagrams or a table to organize your work.
-
The value of a new car decreases by about 15% in the first year. How much will a car be worth after one year if its initial value was $1,000? $5,000? $5,020? \(x\) dollars? If you get stuck, consider using diagrams or a table to organize your work.


Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
If students have a hard time organizing their information, suggest that they use a table.
Students might struggle to write an expression in terms of \(x\). Have students describe in words how they calculated the previous problems with numbers and use that to come up with an expression.
Activity Synthesis
Select students with different ways of writing correct expressions in terms of \(x\) to share their expression. Connect both problems back to the previous work with the distributive property by asking students:
- How else can the first problem be written? (\(x + 0.06x\) or \((1 + 0.06)x\) or \(1.06x\))
- How else can the second problem be written? (\(x - 0.15x\) or \((1 - 0.15)x\) or \(0.85x\))
Design Principle(s): Maximize meta-awareness
5.3: Matching Equations (5 minutes)
Activity
In this activity, students match equations that represent a percent increase situation to the situations they represent.
Launch
Arrange students in groups of 2. 2 minutes of quiet think time followed by 2 minutes of partner discussion.
Student Facing
Match an equation to each of these situations. Be prepared to share your reasoning.
- The water level in a reservoir is now 52 meters. If this was a 23% increase, what was the initial depth?
- The snow is now 52 inches deep. If this was a 77% decrease, what was the initial depth?
\(0.23x = 52\)
\(0.77x = 52\)
\(1.23x = 52\)
\(1.77x = 52\)
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
An astronaut was exploring the moon of a distant planet, and found some glowing goo at the bottom of a very deep crater. She brought a 10-gram sample of the goo to her laboratory. She found that when the goo was exposed to light, the total amount of goo increased by 100% every hour.
- How much goo will she have after 1 hour? After 2 hours? After 3 hours? After \(n\) hours?
- When she put the goo in the dark, it shrank by 75% every hour. How many hours will it take for the goo that was exposed to light for \(n\) hours to return to the original size?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask one or more students to share which equation they matched with each situation, and resolve any discrepancies. Once the matches are agreed upon, ask students how they would solve the equation to find the amount without actually solving the equations.
Design Principle(s): Support sense-making; Optimize output (for explanation)
5.4: Representing Percent Increase and Decrease: Equations (15 minutes)
Optional activity
The purpose of this activity is for students to use equations to represent situations of percent increase and decrease. Additionally, students identify the original and new amount in the double number lines to reinforce what they learned in earlier lessons (that the original amount pertains to 100%).
As students work on the task, look for students who created various equations for the last question.
Launch
Show students the double number line from the activity in the previous lesson.

Help them make connections to the first problem. Tell them that they can go back to the previous lesson to see the double number lines for the others if that helps.
Arrange students in groups of 2. Give 5–8 minutes of quiet work time. After 5 minutes allow students to work with a partner or to continue to work alone.
Supports accessibility for: Conceptual processing; Visual-spatial processing
Student Facing
-
The gas tank in dad’s car holds 12 gallons. The gas tank in mom’s truck holds 50% more than that. How much gas does the truck’s tank hold? Explain why this situation can be represented by the equation \((1.5) \boldcdot 12 = t\). Make sure that you explain what \(t\) represents.
-
Write an equation to represent each of the following situations.
- A movie theater decreased the size of its popcorn bags by 20%. If the old bags held 15 cups of popcorn, how much do the new bags hold?
- After a 25% discount, the price of a T-shirt was $12. What was the price before the discount?
- Compared to last year, the population of Boom Town has increased by 25%.The population is now 6,600. What was the population last year?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may continue to struggle to recognize the original amount and new amount with the proper percentages on the double number line. Remind them that the original amount always corresponds to 100%.
Activity Synthesis
Select students to share the values they identified as original amount and the new amount for a few problems. Discuss how 100% always corresponds to the original value and when there is an increase in the value the new value corresponds to a percentage greater than the original 100%.
Select students to share the different equations they came up with. Discuss how the distributive property is useful for finding the percentage that corresponds with the new value instead of the percentage of the change.
Discuss how solving problems about percent change may require either multiplying or dividing numbers. It can be confusing, but it helps to first express the relationship as an equation and then think about how you can find the unknown number. Looking at the examples below, the first two require multiplication, but the others require division.
Using the structure A% of B is C:
- \((1.5) \boldcdot 12 = c\)
- \((0.80) \boldcdot 15 = c\)
- \(a \boldcdot (1,200) = 1,080\)
- \(a \boldcdot (1.50) = 1.75\)
- \((0.75) \boldcdot b = 12\)
- \((1.25) \boldcdot b = 61, 600\)
Design Principle(s): Optimize output (for generalization); Cultivate conversation
Lesson Synthesis
Lesson Synthesis
Students should feel confident calculating percent increase/decrease using a method of their choice. Ask students:
- “What are some ways we have learned to solve percent increase or percent decrease problems?” (double number lines, tables, equations)
- “Which representation do you prefer to use? Why?”
5.5: Cool-down - Tyler's Savings Bond (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
We can use equations to express percent increase and percent decrease. For example, if \(y\) is 15% more than \(x\),

we can represent this using any of these equations:
\(y = x + 0.15x\)
\(y = (1 + 0.15)x\)
\(y = 1.15x\)
So if someone makes an investment of \(x\) dollars, and its value increases by 15% to \$1250, then we can write and solve the equation \(1.15x =1250\) to find the value of the initial investment.
Here is another example: if \(a\) is 7% less than \(b\),
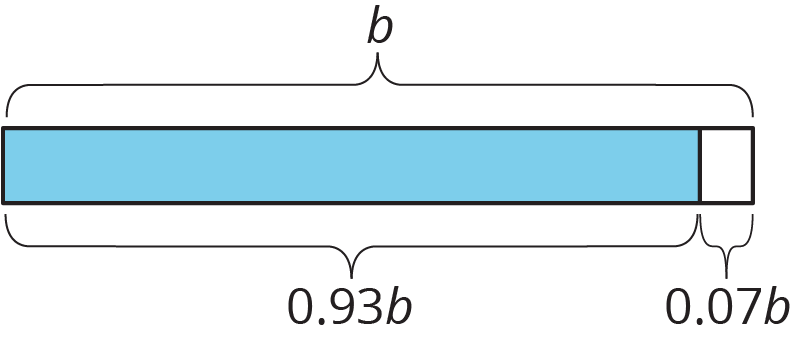
we can represent this using any of these equations:
\(a = b - 0.07b\)
\(a = (1-0.07)b\)
\(a = 0.93b\)
So if the amount of water in a tank decreased 7% from its starting value of \(b\) to its ending value of 348 gallons, then you can write \(0.93b = 348\).
Often, an equation is the most efficient way to solve a problem involving percent increase or percent decrease.