Lesson 3

Defining Equivalent Ratios

View Student Lesson

Problem 1

Each of these is a pair of equivalent ratios. For each pair, explain why they are equivalent ratios or draw a diagram that shows why they are equivalent ratios.

  1. \(4:5\) and \(8:10\)
  2. \(18:3\) and \(6:1\)
  1. \(2:7\) and \(10,\!000:35,\!000\)

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Explain why \(6:4\) and \(18:8\) are not equivalent ratios.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

Are the ratios \(3:6\) and \(6:3\) equivalent? Why or why not?

Solution

For access, consult one of our IM Certified Partners.

Problem 4

This diagram represents 3 batches of light yellow paint. Draw a diagram that represents 1 batch of the same shade of light yellow paint.

A discrete diagram for two quantities labeled "white paint, in cups" and "yellow paint, in cups". The data are as follows: white paint, 9 squares. yellow paint, 15 squares.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 2, Lesson 2.)

Problem 5

In the fruit bowl there are 6 bananas, 4 apples, and 3 oranges.

  1. For every 4 __________________, there are 3 __________________.
  2. The ratio of __________________ to __________________ is \(6:3\).
  3. The ratio of __________________ to __________________ is 4 to 6.
  4. For every 1 orange, there are ______ bananas.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 2, Lesson 1.)

Problem 6

Write fractions for points \(A\) and \(B\) on the number line.

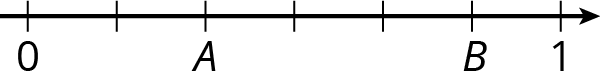
Number line, 7 evenly spaced tick marks, labeled zero, blank, A, blank, blank, B, blank, 1.

Solution

For access, consult one of our IM Certified Partners.

(From Unit 2, Lesson 1.)