Lesson 9

Finding Distances in the Coordinate Plane

Let’s find distances in the coordinate plane.

Problem 1

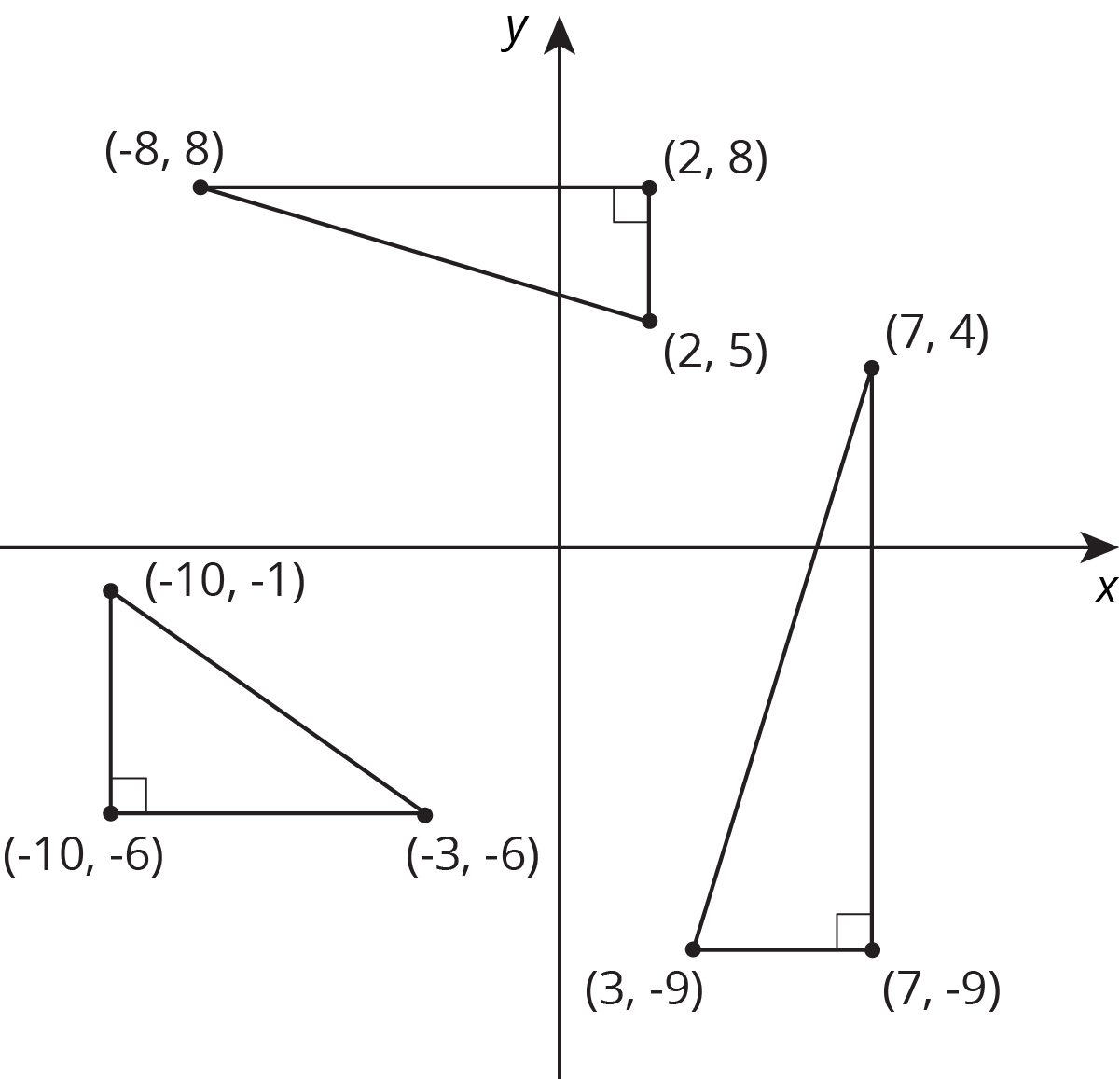
The right triangles are drawn in the coordinate plane, and the coordinates of their vertices are labeled. For each right triangle, label each leg with its length.

3 right triangles on a xy plane.

 

Problem 2

Find the distance between each pair of points. If you get stuck, try plotting the points on graph paper.

  1. \(M=(0,\text-11)\) and \(P=(0,2)\)
  2. \(A=(0,0)\) and \(B=(\text-3, \text-4)\)

  3. \(C=(8,0)\) and \(D=(0, \text-6)\)

Problem 3

  1. Find an object that contains a right angle. This can be something in nature or something that was made by humans or machines.
  2. Measure the two sides that make the right angle. Then measure the distance from the end of one side to the end of the other.
  3. Draw a diagram of the object, including the measurements. 
  4. Use the Pythagorean Theorem to show that your object really does have a right angle.
(From Unit 8, Lesson 7.)

Problem 4

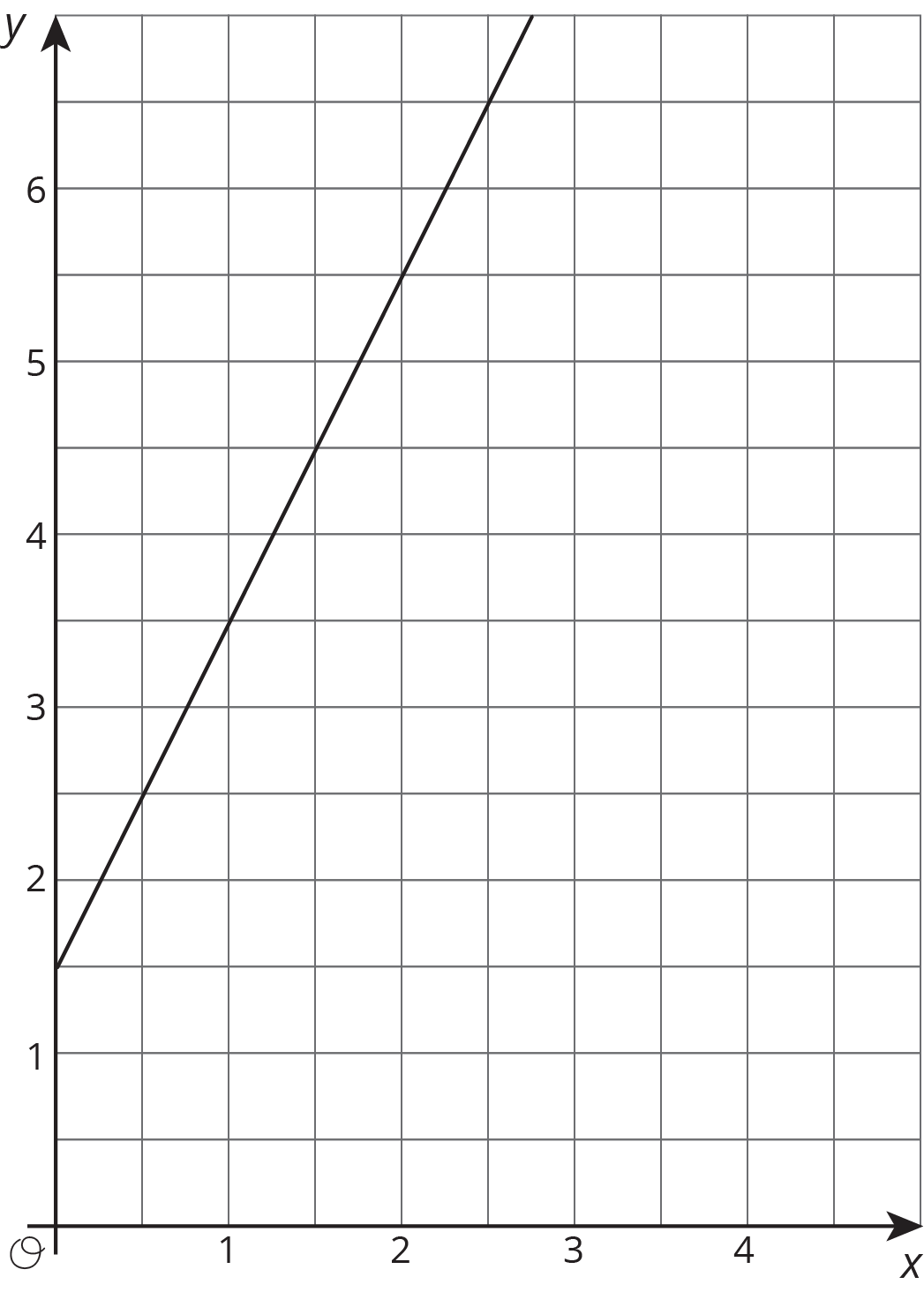
Which line has a slope of 0.625, and which line has a slope of 1.6? Explain why the slopes of these lines are 0.625 and 1.6.

Two lines on a grid that intersect at a point. 2nd point on Top line is 8 up and 5 right from 1st point. 2nd point on bottom line is 5 up and 8 right from 1st point.

 

(From Unit 2, Lesson 15.)

Problem 5

Write an equation for the graph.

Horizontal axis, 0 to 4, 1’s. Vertical axis, 0 to 6, 1’s. Line with slope=2, y intercept =1.5.

(From Unit 5, Lesson 6.)