Lesson 11
Decimal Representations of Rational Numbers
Let’s learn more about how rational numbers can be represented.
11.1: Notice and Wonder: Shaded Bars
What do you notice? What do you wonder?
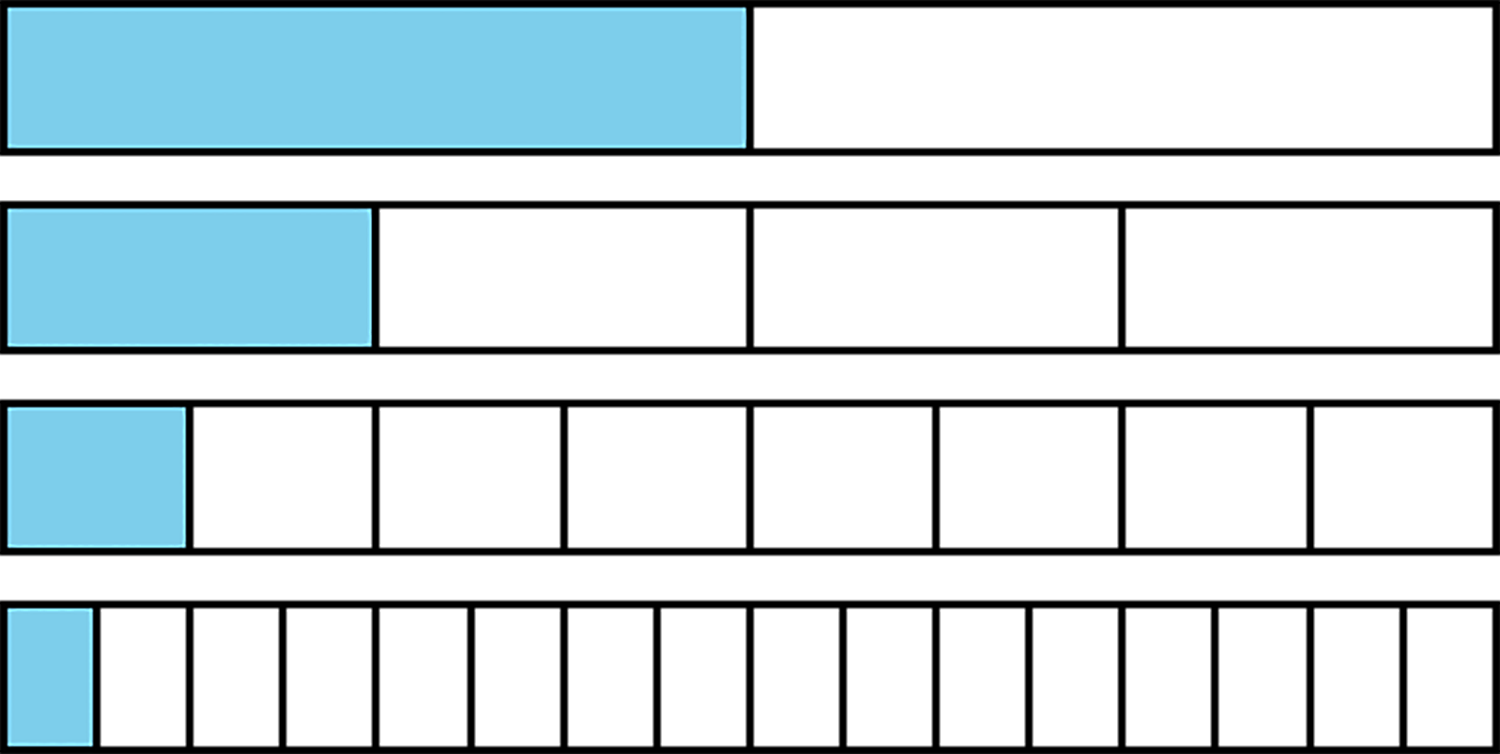
11.2: Halving the Length
Here is a number line from 0 to 1.

- Mark the midpoint between 0 and 1. What is the decimal representation of that number?
- Mark the midpoint between 0 and the newest point. What is the decimal representation of that number?
- Repeat step two. How did you find the value of this number?
- Describe how the value of the midpoints you have added to the number line keep changing as you find more. How do the decimal representations change?
11.3: Recalculating Rational Numbers
-
Rational numbers are fractions and their opposites. All of these numbers are rational numbers. Show that they are rational by writing them in the form \(\frac{a}{b}\) or \(\text -\frac{a}{b}\).
- 0.2
- \(\text -\sqrt{4}\)
- 0.333
- \(\sqrt[3]{1000}\)
- -1.000001
-
\(\sqrt{\frac19}\)
-
All rational numbers have decimal representations, too. Find the decimal representation of each of these rational numbers.
- \(\frac38\)
- \(\frac75\)
- \(\frac{999}{1000}\)
- \(\frac{111}{2}\)
- \(\sqrt[3]{\frac18}\)
11.4: Zooming In On $\frac{2}{11}$
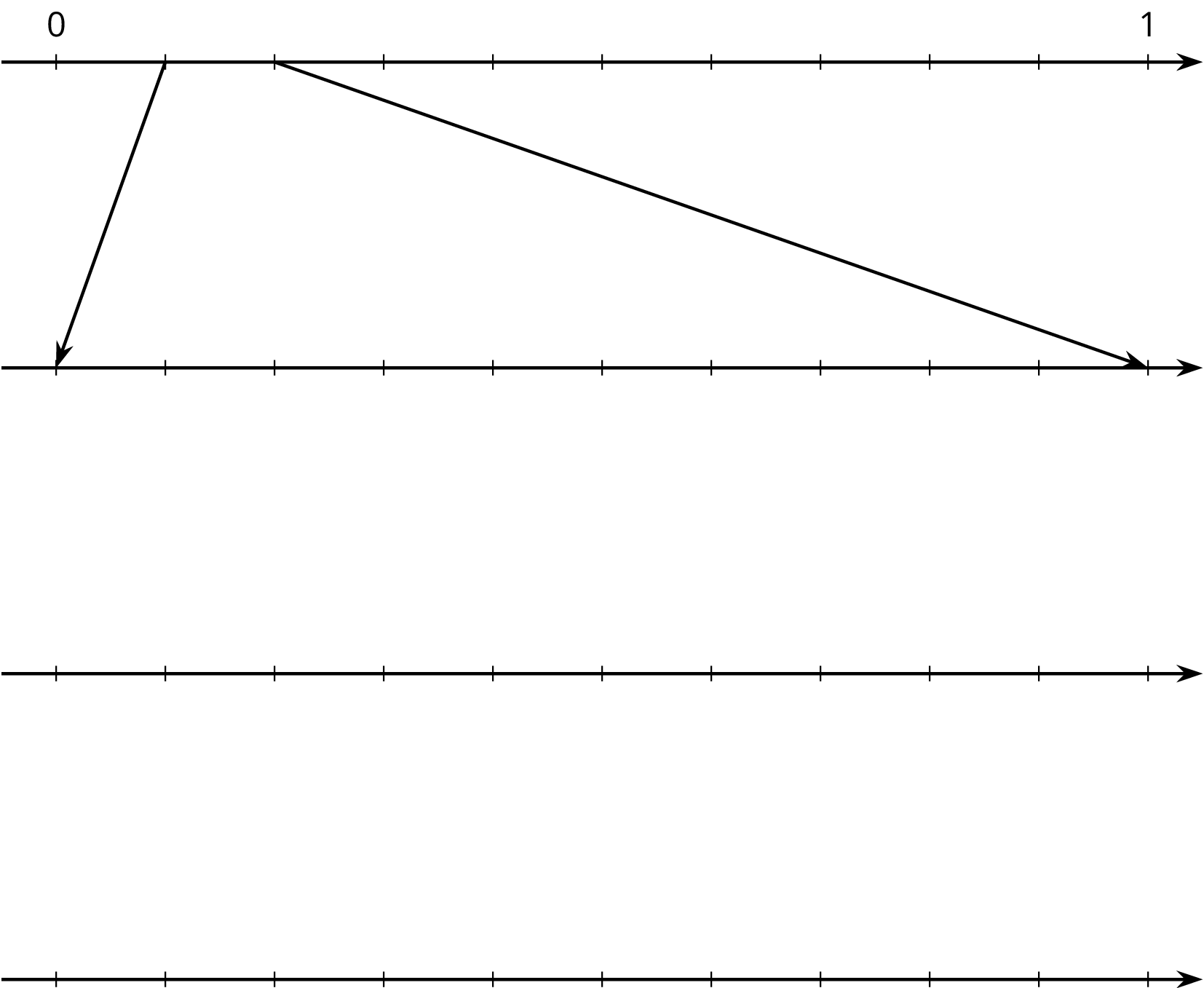
-
On the topmost number line, label the tick marks. Next, find the first decimal place of \(\frac{2}{11}\) using long division and estimate where \(\frac{2}{11}\) should be placed on the top number line.
-
Label the tick marks of the second number line. Find the next decimal place of \(\frac{2}{11}\) by continuing the long division and estimate where \(\frac{2}{11}\) should be placed on the second number line. Add arrows from the second to the third number line to zoom in on the location of \(\frac{2}{11}\).
-
Repeat the earlier step for the remaining number lines.
- What do you think the decimal expansion of \(\frac{2}{11}\) is?
Let \(x=\frac{25}{11}=2.272727. . . \) and \(y=\frac{58}{33}=1.75757575. . .\)
For each of the following questions, first decide whether the fraction or decimal representations of the numbers are more helpful to answer the question, and then find the answer.
- Which of \(x\) or \(y\) is closer to 2?
-
Find \(x^2\).
Summary
We learned earlier that rational numbers are a fraction or the opposite of a fraction. For example, \(\frac34\) and \(\text-\frac52\) are both rational numbers. A complicated-looking numerical expression can also be a rational number as long as the value of the expression is a positive or negative fraction. For example, \(\sqrt{64}\) and \(\text-\sqrt[3]{\frac18}\) are rational numbers because \(\sqrt{64} = 8\) and \(\text-\sqrt[3]{\frac18} = \text-\frac12\).
Rational numbers can also be written using decimal notation. Some have finite decimal expansions, like 0.75, -2.5, or -0.5. Other rational numbers have infinite decimal expansions, like 0.7434343 . . . where the 43s repeat forever. To avoid writing the repeating part over and over, we use the notation \(0.7\overline{43}\) for this number. The bar over part of the expansion tells us the part which is to repeat forever.
A decimal expansion of a number helps us plot it accurately on a number line divided into tenths. For example, \(0.7\overline{43}\) should be between 0.7 and 0.8. Each further decimal digit increases the accuracy of our plotting. For example, the number \(0.7\overline{43}\) is between 0.743 and 0.744.
Glossary Entries
- cube root
The cube root of a number \(n\) is the number whose cube is \(n\). It is also the edge length of a cube with a volume of \(n\). We write the cube root of \(n\) as \(\sqrt[3]{n}\).
For example, the cube root of 64, written as \(\sqrt[3]{64}\), is 4 because \(4^3\) is 64. \(\sqrt[3]{64}\) is also the edge length of a cube that has a volume of 64.
- repeating decimal
A repeating decimal has digits that keep going in the same pattern over and over. The repeating digits are marked with a line above them.
For example, the decimal representation for \(\frac13\) is \(0.\overline{3}\), which means 0.3333333 . . . The decimal representation for \(\frac{25}{22}\) is \(1.1\overline{36}\) which means 1.136363636 . . .