Lesson 6
What about Other Bases?
Let’s explore exponent patterns with bases other than 10.
Problem 1
Priya says “I can figure out \(5^0\) by looking at other powers of 5. \(5^3\) is 125, \(5^2\) is 25, then \(5^1\) is 5.”
- What pattern do you notice?
- If this pattern continues, what should be the value of \(5^0\)? Explain how you know.
- If this pattern continues, what should be the value of \(5^{\text-1}\)? Explain how you know.
Problem 2
Select all the expressions that are equivalent to \(4^{\text-3}\).
A:
-12
B:
\(2^{\text-6}\)
C:
\(\frac{1}{4^3}\)
D:
\(\left(\frac{1}{4}\right) \boldcdot \left(\frac{1}{4}\right) \boldcdot \left(\frac{1}{4}\right)\)
E:
12
F:
\((\text-4) \boldcdot (\text-4) \boldcdot (\text-4)\)
G:
\(\frac{8^{\text-1}}{2^2}\)
Problem 3
Write each expression using a single exponent.
- \(\frac{5^3}{5^6}\)
- \((14^3)^6\)
- \(8^3 \boldcdot 8^6\)
- \(\frac{16^6}{16^3}\)
- \((21^3)^{\text-6}\)
Problem 4
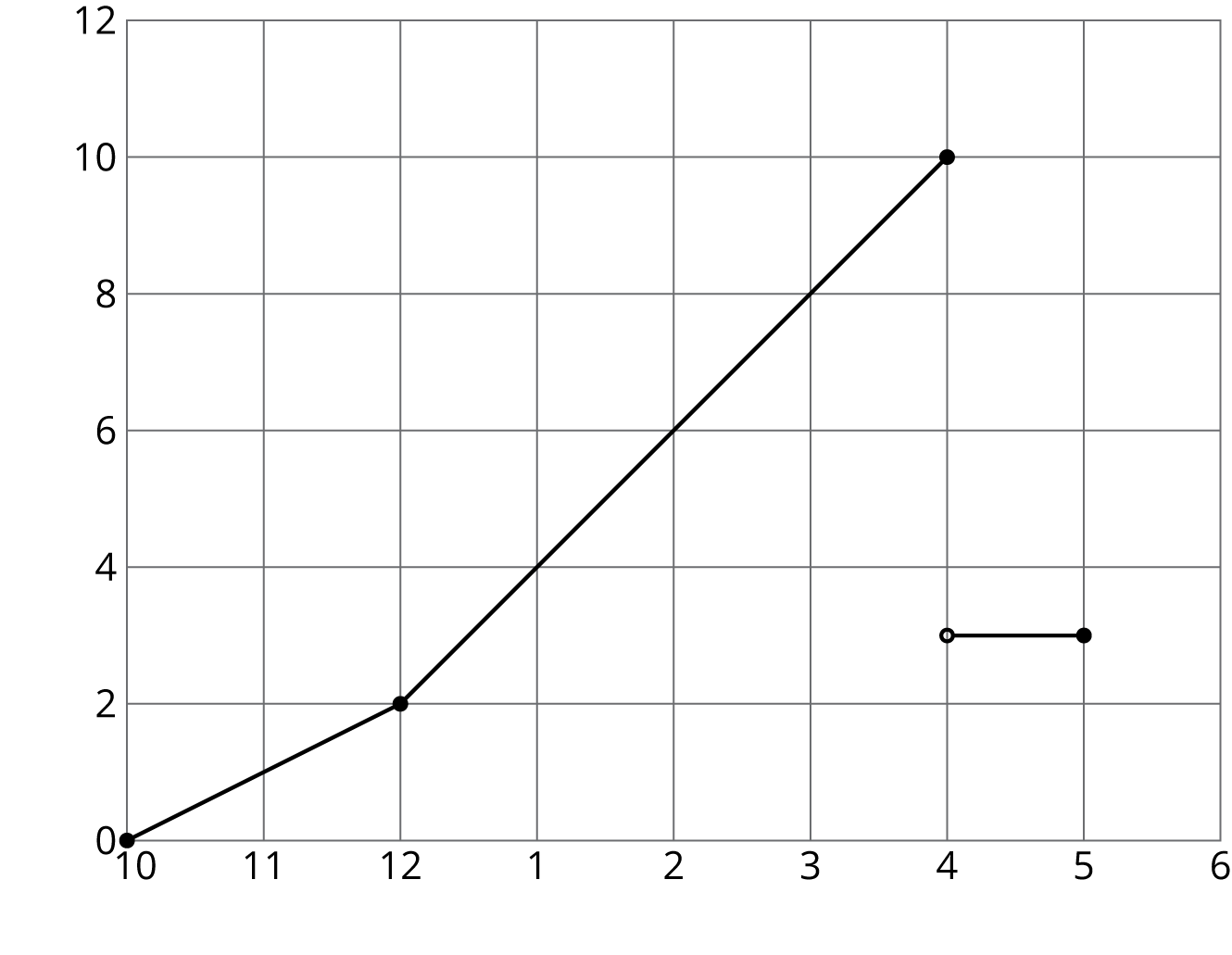
Andre sets up a rain gauge to measure rainfall in his back yard. On Tuesday, it rains off and on all day.
- He starts at 10 a.m. with an empty gauge when it starts to rain.
- Two hours later, he checks, and the gauge has 2 cm of water in it.
- It starts raining even harder, and at 4 p.m., the rain stops, so Andre checks the rain gauge and finds it has 10 cm of water in it.
- While checking it, he accidentally knocks the rain gauge over and spills most of the water, leaving only 3 cm of water in the rain gauge.
- When he checks for the last time at 5 p.m., there is no change.
Graph A
Graph B
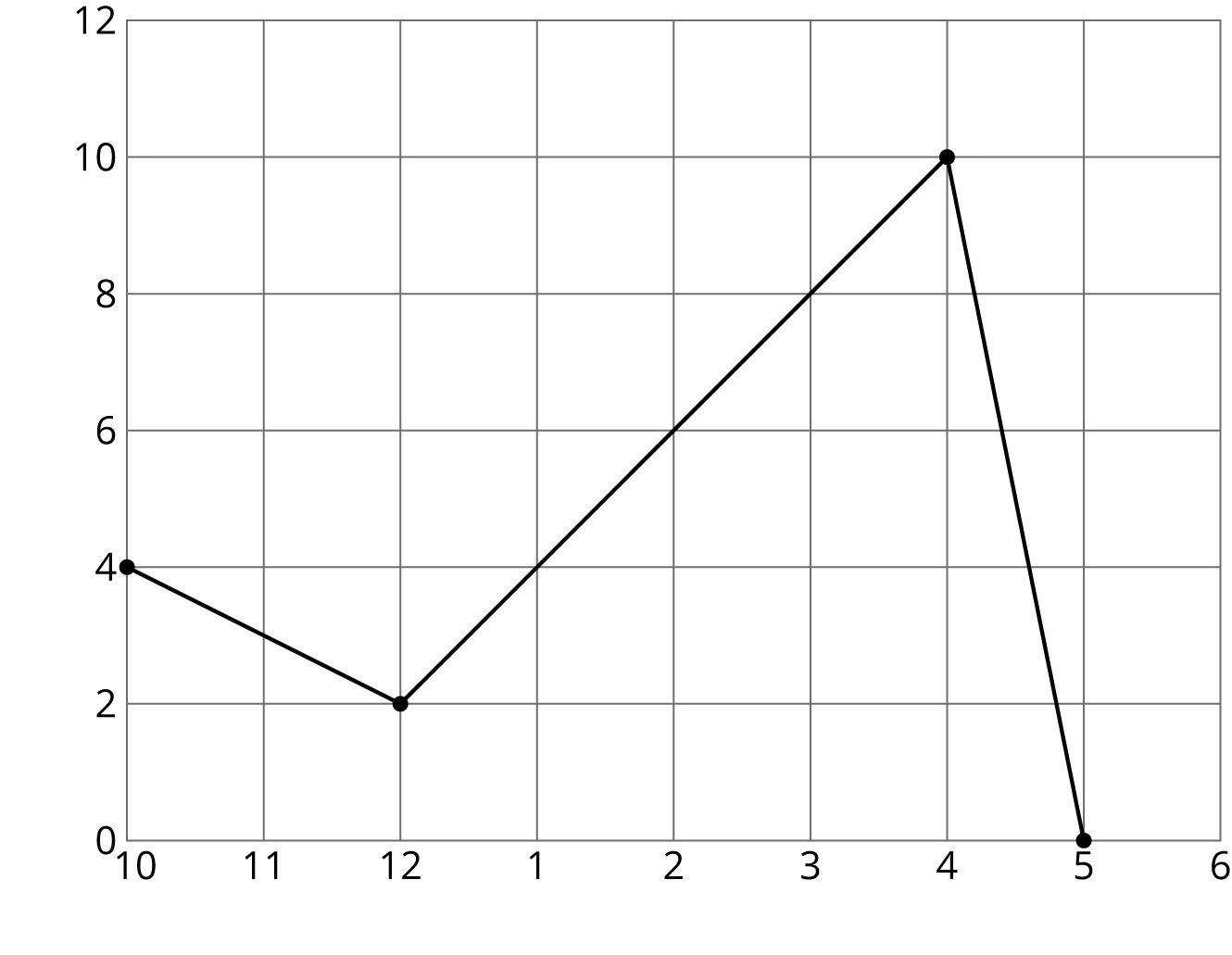
- Which of the two graphs could represent Andre’s story? Explain your reasoning.
- Label the axes of the correct graph with appropriate units.
- Use the graph to determine how much total rain fell on Tuesday.