Lesson 11

Representing Small Numbers on the Number Line

Let’s visualize small numbers on the number line using powers of 10.

11.1: Small Numbers on a Number Line

Kiran drew this number line.

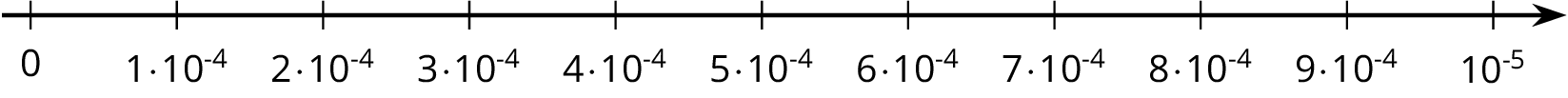
A number line.

Andre said, “That doesn’t look right to me.”

Explain why Kiran is correct or explain how he can fix the number line.

 

11.2: Comparing Small Numbers on a Number Line

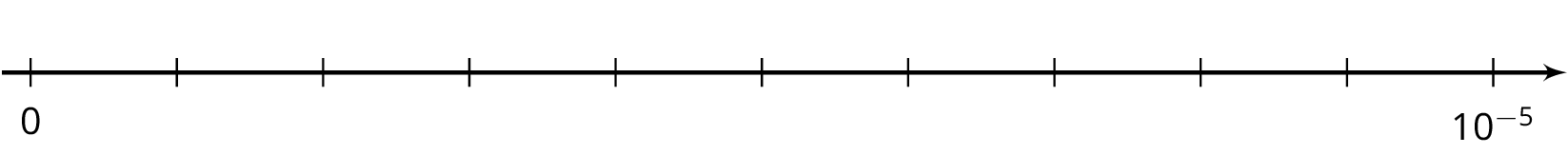
A number line, 11 tick marks, 0, 9 blank tick marks, 10 to the negative 5 power.

  1. Label the tick marks on the number line.

  2. Plot the following numbers on the number line:

    A. \(6 \boldcdot 10^{\text -6}\)

    B. \(6 \boldcdot 10^{\text -7}\)

    C. \(29 \boldcdot 10^{\text -7}\)

    D. \((0.7) \boldcdot 10^{\text -5}\)

  3. Which is larger, \(29 \boldcdot 10^{\text -7}\) or \(6 \boldcdot 10^{\text -6}\)? Estimate how many times larger.
  4. Which is larger, \(7 \boldcdot 10^{\text -8}\) or \(3 \boldcdot 10^{\text -9}\)? Estimate how many times larger.

11.3: Atomic Scale

  1. The radius of an electron is about 0.0000000000003 cm.

    1. Write this number as a multiple of a power of 10.

    2. Decide what power of 10 to put on the right side of this number line and label it.

    3. Label each tick mark as a multiple of a power of 10.

      A number line with eleven evenly spaced tick marks. The first tick is labeled 0, the last tick is labeled 10 to the blank power, and the remaining tick marks are blank.

    4. Plot the radius of the electron in centimeters on the number line.

  2. The mass of a proton is about 0.0000000000000000000000017 grams.

    1. Write this number as a multiple of a power of 10.

    2. Decide what power of 10 to put on the right side of this number line and label it.

    3. Label each tick mark as a multiple of a power of 10.

      A number line with eleven evenly spaced tick marks. The first tick is labeled 0, the last tick is labeled 10 to the blank power, and the remaining tick marks are blank.

    4. Plot the mass of the proton in grams on the number line.

  3. Point \(A\) on the zoomed-in number line describes the wavelength of a certain X-ray in meters.
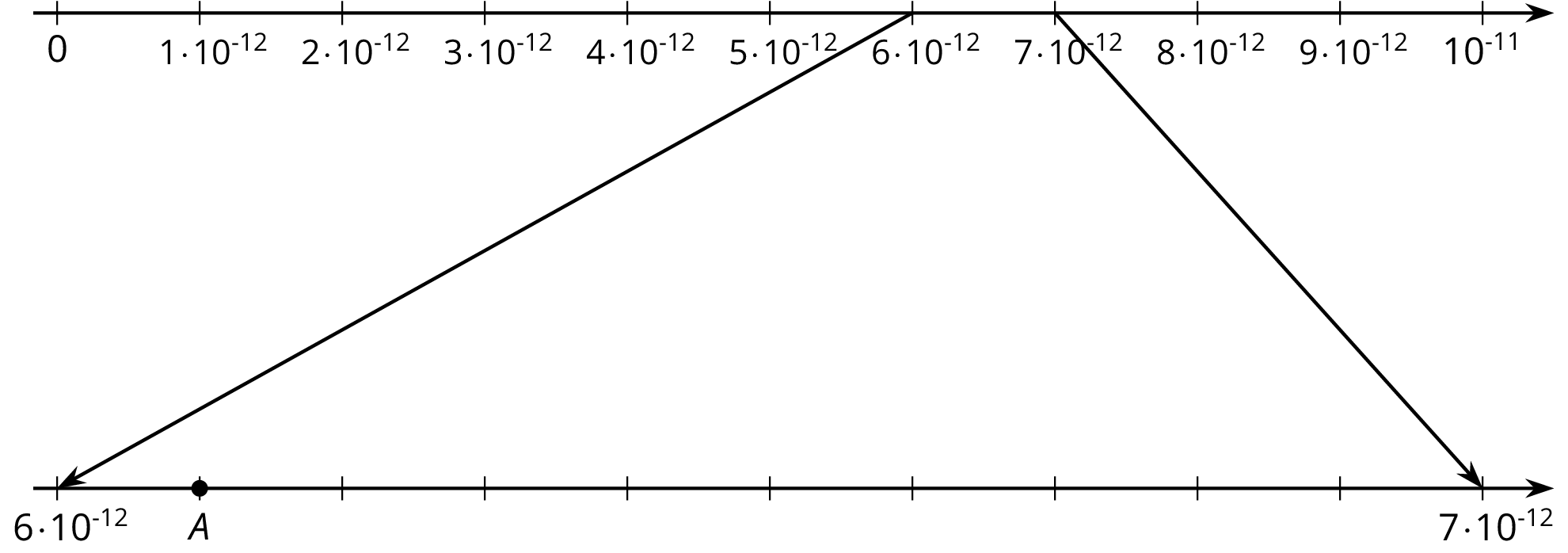
    A number line.
    1. Write the wavelength of the X-ray as a multiple of a power of 10.
    2. Write the wavelength of the X-ray as a decimal.

Summary

The width of a bacterium cell is about \(\displaystyle 2 \boldcdot 10^{\text -6}\) meters. If we want to plot this on a number line, we need to find which two powers of 10 it lies between. We can see that \(2 \boldcdot 10^{\text -6}\) is a multiple of \(10^{\text -6}\). So our number line will be labeled with multiples of \(\displaystyle 10^{\text -6}\)

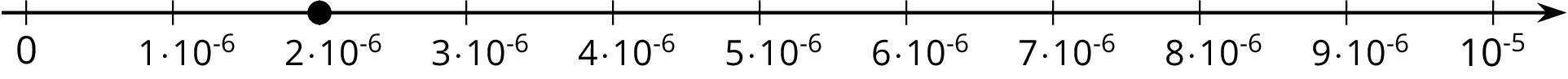
A number line.

Note that the right side is labeled \(\displaystyle 10 \boldcdot 10^{\text -6} =10^{\text -5}\)

The power of ten on the right side of the number line is always greater than the power on the left. This is true for powers with positive or negative exponents.